Kapasitans - Capacitance

Vanlige symboler	C
SI -enhet	farad
Andre enheter	μF, nF, pF
I SI -baseenheter	F = A 2 s 4 kg −1 m −2
Avledninger fra andre mengder	C = ladning / spenning
Dimensjon	M −1 L −2 T 4 I 2

Artikler om
Elektromagnetisme
Elektrisitet Magnetisme Historie Lærebøker
Elektrostatikk Elektrisk ladning Coulombs lov Dirigent Ladetetthet Tillatelse Elektrisk dipolmoment Elektrisk felt Elektrisk potensial Elektrisk strøm  / potensiell energi Støt fra statisk elektrisitet Gauss lov Induksjon Isolering Polarisasjonstetthet Statisk elektrisitet Triboelektrisitet
Magnetostatikk Amperes lov Biot - Savart -loven Gauss lov for magnetisme Magnetfelt Magnetisk flux Magnetisk dipolmoment Magnetisk permeabilitet Magnetisk skalarpotensial Magnetisering Magnetomotiv kraft Magnetisk vektorpotensial Høyre-regelen
Elektrodynamikk Lorentz tvangsrett Elektromagnetisk induksjon Faradays lov Lenz lov Forskyvningsstrøm Maxwells ligninger Elektromagnetisk felt Elektromagnetisk puls Elektromagnetisk stråling Maxwell tensor Poynting vektor Liénard - Wiechert potensial Jefimenkos ligninger virvelstrøm London ligninger Matematiske beskrivelser av det elektromagnetiske feltet
Elektrisk nett Vekselstrøm Kapasitans Likestrøm Elektrisk strøm Elektrolyse Nåværende tetthet Joule oppvarming Elektromotorisk kraft Impedans Induktans Ohms lov Parallell krets Motstand Resonant hulrom Seriekrets Spenning Bølgeledere
Kovariant formulering Elektromagnetisk tensor ( stress - energi tensor ) Firestrøm Elektromagnetisk firepotensial
Forskere Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Henry Hertz Joule Lenz Lorentz Maxwell Ørsted Ohm Ritchie Savart Sanger Tesla Volta Weber Poisson
v t e

Kapasitans er forholdet mellom mengden elektrisk ladning lagret på en leder og en forskjell i elektrisk potensial . Det er to nært beslektede forestillinger om kapasitans: selvkapasitans og gjensidig kapasitans . Ethvert objekt som kan være elektrisk ladet utviser selvkapasitans . I dette tilfellet måles den elektriske potensialforskjellen mellom objektet og bakken. Et materiale med stor selvkapasitans holder mer elektrisk ladning ved en gitt potensialforskjell enn et med lav kapasitans. Tanken om gjensidig kapasitans er spesielt viktig for å forstå kondensatorens operasjoner , en av de tre elementære lineære elektroniske komponentene (sammen med motstander og induktorer ). I en typisk kondensator brukes to ledere til å skille elektrisk ladning, med en leder som er positivt ladet og den andre negativt ladet, men systemet har en total ladning på null. Forholdet i dette tilfellet er størrelsen på den elektriske ladningen på hver leder og potensialforskjellen er den som måles mellom de to lederne.

Kapasitansen er bare en funksjon av konstruksjonens geometri (f.eks. Platens område og avstanden mellom dem) og permittiviteten til det dielektriske materialet mellom platene på kondensatoren. For mange dielektriske materialer er permittiviteten og dermed kapasitansen uavhengig av potensialforskjellen mellom lederne og den totale ladningen på dem.

Den SI enhet for kapasitans er farad (symbol: F), oppkalt etter den engelske fysikeren Michael Faraday . En 1 farad kondensator, når den er ladet med 1 coulomb elektrisk ladning, har en potensialforskjell på 1 volt mellom platene. Kapasitansens gjensidige kalles elastans .

Selvkapasitans

I elektriske kretser er begrepet kapasitans vanligvis en forkortelse for gjensidig kapasitans mellom to tilstøtende ledere, for eksempel de to platene på en kondensator. For en isolert leder eksisterer det imidlertid også en egenskap som kalles selvkapasitans , som er mengden elektrisk ladning som må tilføres en isolert leder for å øke det elektriske potensialet med en enhet (dvs. en volt, i de fleste målesystemer). Referansepunktet for dette potensialet er en teoretisk hulledende sfære, med uendelig radius, med lederen sentrert inne i denne sfæren.

Matematisk, den selv kapasitans er av et leder definert av

${\ displaystyle C = {\ frac {q} {V}},}$

hvor

q er belastningen på lederen,

${\ displaystyle V = {1 \ over 4 \ pi \ varepsilon _ {0}} \ int {\ sigma \ over r} \, dS}$ er det elektriske potensialet,

σ er overflateladningstettheten.

dS er et infinitesimalt arealelement på lederens overflate,

r er lengden fra dS til et fast punkt M på lederen

${\ displaystyle \ varepsilon _ {0}}$er vakuumpermittiviteten

Ved å bruke denne metoden er selvkapasitansen til en ledende sfære med radius R :

${\ displaystyle C = 4 \ pi \ varepsilon _ {0} R \,}$

Eksempelverdier for selvkapasitans er:

• for den øverste "platen" på en van de Graaff -generator , vanligvis en sfære på 20 cm i radius: 22,24 pF,
• planeten Jorden : ca 710 µF.

Mellomviklingskapasitansen til en spole kalles noen ganger selvkapasitans, men dette er et annet fenomen. Det er faktisk gjensidig kapasitans mellom spolens individuelle svinger og er en form for villfarlig eller parasittisk kapasitans . Denne selvkapasitansen er en viktig faktor ved høye frekvenser: Den endrer spolens impedans og gir opphav til parallell resonans . I mange applikasjoner er dette en uønsket effekt og setter en øvre frekvensgrense for korrekt drift av kretsen.

Gjensidig kapasitans

En vanlig form er en parallell-plate kondensator , som består av to ledende plater er isolert fra hverandre, vanligvis sandwiching et dielektrisk materiale. I en parallellplatekondensator er kapasitansen svært nær proporsjonal med overflaten på lederplatene og omvendt proporsjonal med separasjonsavstanden mellom platene.

Hvis ladningene på platene er + q og - q , og V gir spenningen mellom platene, er kapasitansen C gitt av

${\ displaystyle C = {\ frac {q} {V}}.}$

som gir den spenning / strøm forholdet

${\ displaystyle i (t) = C {\ frac {\ mathrm {d} v (t)} {\ mathrm {d} t}},}$

hvor d v ( t )/d t er den øyeblikkelige spenningsendringen.

Energien lagret i en kondensator blir funnet ved å integrere arbeidet W :

${\ displaystyle W _ {\ text {lading}} = {\ frac {1} {2}} CV^{2}}$

Kapasitansmatrise

Diskusjonen ovenfor er begrenset til to ledende plater, men av vilkårlig størrelse og form. Definisjonen gjelder ikke når det er mer enn to ladede plater, eller når nettoladningen på de to platene er ikke-null. For å håndtere denne saken introduserte Maxwell sine potensialkoeffisienter . Hvis tre (nesten ideelle) ledere får ladninger , blir spenningen ved leder 1 gitt av ${\ displaystyle C = Q/V}$${\ displaystyle Q_ {1}, Q_ {2}, Q_ {3}}$

${\ displaystyle V_ {1} = P_ {11} Q_ {1}+P_ {12} Q_ {2}+P_ {13} Q_ {3},}$

og på samme måte for de andre spenningene. Hermann von Helmholtz og Sir William Thomson viste at potensialkoeffisientene er symmetriske, slik at osv. Dermed kan systemet beskrives med en samling koeffisienter kjent som elastansmatrisen eller gjensidig kapasitansmatrise , som er definert som: ${\ displaystyle P_ {12} = P_ {21}}$

${\ displaystyle P_ {ij} = {\ frac {\ partiell V_ {i}} {\ delvis Q_ {j}}}}$

Fra dette kan den gjensidige kapasitansen mellom to objekter defineres ved å løse den totale ladningen Q og bruke . ${\ displaystyle C_ {m}}$${\ displaystyle C_ {m} = Q/V}$

${\ displaystyle C_ {m} = {\ frac {1} {(P_ {11}+P_ {22})-(P_ {12}+P_ {21})}}}}}$

Siden ingen faktisk enhet har helt like og motsatte ladninger på hver av de to "platene", er det gjensidig kapasitans som rapporteres på kondensatorer.

Samlingen av koeffisienter er kjent som kapasitansmatrisen , og er inversen av elastansmatrisen. ${\ displaystyle C_ {ij} = {\ frac {\ partiell Q_ {i}} {\ delvis V_ {j}}}}$

Kondensatorer

Kapasitansen til de fleste kondensatorer som brukes i elektroniske kretser er generelt flere størrelsesordener mindre enn faraden . De vanligste underenhetene for kapasitans som brukes i dag er mikrofarad (µF), nanofarad (nF), picofarad (pF) og i mikrokretser femtofarad (fF). Imidlertid, spesielt laget superkondensatorer kan være mye større (så mye som flere hundre farad), og parasittiske kapasitive elementer kan være mindre enn en femtofarad. Tidligere ble alternative underenheter brukt i gamle historiske tekster; "mf" og "mfd" for mikrofarad (µF); "mmf", "mmfd", "pfd", "µµF" for picofarad (pF); men regnes nå som foreldet.

Kapasitans kan beregnes hvis geometrien til lederne og de dielektriske egenskapene til isolatoren mellom lederne er kjent. En kvalitativ forklaring på dette kan gis som følger.
Når en positiv ladning er satt til en leder, skaper denne ladningen et elektrisk felt, som avviser enhver annen positiv ladning som skal flyttes til lederen; dvs. å øke den nødvendige spenningen. Men hvis det er en annen leder med en negativ ladning i nærheten, svekkes det elektriske feltet til den positive lederen som avviser den andre positive ladningen (den andre positive ladningen kjenner også tiltrekningskraften til den negative ladningen). Så på grunn av den andre lederen med en negativ ladning, blir det lettere å legge en positiv ladning på den allerede positive ladede første lederen, og omvendt; dvs. at den nødvendige spenningen senkes.
Som et kvantitativt eksempel kan du vurdere kapasitansen til en kondensator konstruert av to parallelle plater begge av område A atskilt med en avstand d . Hvis d er tilstrekkelig liten med hensyn til det minste akkordet til A , holder det til et høyt nøyaktighetsnivå:

${\ displaystyle \ C = \ varepsilon _ {0} {\ frac {A} {d}}}$

hvor

C er kapasitansen, i farads;

A er området for overlapping av de to platene, i kvadratmeter;

ε ₀ er den elektriske konstanten ( ε ₀  ≈8,854 × 10 ⁻¹²  F⋅m ⁻¹ ); og

d er skillet mellom platene, i meter;

Kapasitans er proporsjonal med området for overlapping og omvendt proporsjonal med separasjonen mellom ledende ark. Jo nærmere arkene er til hverandre, desto større er kapasitansen. Ligningen er en god tilnærming hvis d er liten sammenlignet med platens andre dimensjoner slik at det elektriske feltet i kondensatorområdet er jevnt, og det såkalte frynsefeltet rundt periferien gir bare et lite bidrag til kapasitansen.

Ved å kombinere ligningen for kapasitans med ligningen ovenfor for energien lagret i en kapasitans, for en flat-platekondensator er energien som er lagret:

${\ displaystyle W _ {\ text {lagret}} = {\ frac {1} {2}} CV^{2} = {\ frac {1} {2}} \ varepsilon _ {0} {\ frac {A} {d}} V^{2}.}$

hvor W er energien, i joule; C er kapasitansen, i farads; og V er spenningen, i volt.

Stray kapasitans

Alle to tilstøtende ledere kan fungere som en kondensator, selv om kapasitansen er liten med mindre lederne er tett sammen for lange avstander eller over et stort område. Denne (ofte uønskede) kapasitansen kalles parasittisk eller "herreløs kapasitans". Stray -kapasitans kan tillate signaler å lekke mellom ellers isolerte kretser (en effekt som kalles krysstale ), og det kan være en begrensende faktor for at kretsene skal fungere ved høy frekvens .

Stray -kapasitans mellom inngang og utgang i forsterkerkretser kan være plagsom fordi den kan danne en vei for tilbakemelding , noe som kan forårsake ustabilitet og parasittisk svingning i forsterkeren. Det er ofte praktisk for analytiske formål å erstatte denne kapasitansen med en kombinasjon av en inngang-til-jord kapasitans og en utgang til jord kapasitans; den opprinnelige konfigurasjonen-inkludert inngang-til-utgangskapasitansen-blir ofte referert til som en pi-konfigurasjon. Millers teorem kan brukes til å utføre denne erstatningen: den sier at hvis forsterkningsforholdet på to noder er 1 / K , kan en impedans av Z som forbinder de to nodene erstattes med en Z / (1 -  K ) impedans mellom første node og bakken og en KZ /( K  - 1) impedans mellom den andre noden og bakken. Siden impedansen varierer omvendt med kapasitans, erstattes internodekapasitansen, C , med en kapasitans på KC fra inngang til jord og en kapasitans på ( K  - 1) C / K fra utgang til bakke. Når inngang-til-utgang-forsterkningen er veldig stor, er ekvivalent inngang-til-jord-impedans veldig liten, mens utgang-til-jord-impedansen er i hovedsak lik den opprinnelige (inngang-til-utgang) impedansen.

Kapasitans for ledere med enkle former

Beregning av kapasitansen til et system innebærer å løse Laplace-ligningen ∇ ² φ = 0 med et konstant potensial φ på den 2-dimensjonale overflaten til lederne innebygd i 3-mellomrom. Dette er forenklet av symmetrier. Det er ingen løsning når det gjelder elementære funksjoner i mer kompliserte saker.

For plane situasjoner kan analytiske funksjoner brukes til å kartlegge forskjellige geometrier til hverandre. Se også Schwarz - Christoffel kartlegging .

Kapasitet for enkle systemer

Type	Kapasitans	Kommentar
Parallellplate kondensator	${\ displaystyle \ varepsilon A/d}$	ε : Permittivity
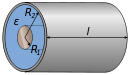
Konsentriske sylindere	${\ displaystyle {\ frac {2 \ pi \ varepsilon \ ell} {\ ln \ venstre (R_ {2}/R_ {1} \ høyre)}}}}$	ε : Permittivity
Par parallelle ledninger	${\ displaystyle {\ frac {\ pi \ varepsilon \ ell} {\ operatorname {arcosh} \ left ({\ frac {d} {2a}} \ right)}} = {\ frac {\ pi \ varepsilon \ ell} {\ ln \ venstre ({\ frac {d} {2a}}+{\ sqrt {{\ frac {d^{2}} {4a^{2}}}-1}} \ høyre)}}}}$
Ledning parallelt med veggen	${\ displaystyle {\ frac {2 \ pi \ varepsilon \ ell} {\ operatorname {arcosh} \ left ({\ frac {d} {a}} \ right)}} = {\ frac {2 \ pi \ varepsilon \ ell} {\ ln \ venstre ({\ frac {d} {a}}+{\ sqrt {{\ frac {d^{2}} {a^{2}}}-1}} \ høyre)}} }$	a : Ledningsradius d : Avstand, d> a ℓ : Ledningslengde
To parallelle koplanære strimler	${\ displaystyle \ varepsilon \ ell {\ frac {K \ left ({\ sqrt {1-k^{2}}} \ right)} {K \ left (k \ right)}}}$	d : Avstand w 1 , w 2 : Stripebredde k m : d/(2w m +d) k 2 : k 1 k 2 K : Komplett elliptisk integral av den første typen ℓ : Lengde
Konsentriske kuler	${\ displaystyle {\ frac {4 \ pi \ varepsilon} {{\ frac {1} {R_ {1}}}-{\ frac {1} {R_ {2}}}}}}}$	ε : Permittivity
To kuler, like radius	${\ displaystyle 2 \ pi \ varepsilon a \ sum _ {n = 1}^{\ infty} {\ frac {\ sinh \ left (\ ln \ left (D+{\ sqrt {D^{2} -1}} \ høyre) \ høyre)} {\ sinh \ venstre (n \ ln \ venstre (D+{\ sqrt {D^{2} -1}} \ høyre) \ høyre)}}}}$ ${\ displaystyle = 2 \ pi \ varepsilon a \ left \ {1+{\ frac {1} {2D}}+{\ frac {1} {4D^{2}}}+{\ frac {1} {8D ^{3}}}+{\ frac {1} {8D^{4}}}+{\ frac {3} {32D^{5}}}+O \ venstre ({\ frac {1} {D^ {6}}} \ right) \ right \}}$ ${\ displaystyle = 2 \ pi \ varepsilon a \ left \ {\ ln 2+ \ gamma-{\ frac {1} {2}} \ ln \ left (2D-2 \ right)+O \ left (2D-2 \ right) \ right \}}$	a : Radius d : Avstand, d > 2 a D = d /2 a , D > 1 γ : Eulers konstant
Kule foran veggen	${\ displaystyle 4 \ pi \ varepsilon a \ sum _ {n = 1}^{\ infty} {\ frac {\ sinh \ left (\ ln \ left (D+{\ sqrt {D^{2} -1}} \ høyre) \ høyre)} {\ sinh \ venstre (n \ ln \ venstre (D+{\ sqrt {D^{2} -1}} \ høyre) \ høyre)}}}}$	${\ displaystyle a}$: Radius : Avstand, ${\ displaystyle d}$${\ displaystyle d> a}$ ${\ displaystyle D = d/a}$
Sfæren	${\ displaystyle 4 \ pi \ varepsilon a}$	${\ displaystyle a}$: Radius
Sirkulær plate	${\ displaystyle 8 \ varepsilon a}$	${\ displaystyle a}$: Radius
Tynn rett tråd, endelig lengde	${\ displaystyle {\ frac {2 \ pi \ varepsilon \ ell} {\ Lambda}} \ venstre \ {1+{\ frac {1} {\ Lambda}} \ venstre (1- \ ln 2 \ høyre)+{ \ frac {1} {\ Lambda ^{2}}} \ venstre [1+ \ venstre (1- \ ln 2 \ høyre) ^{2}-{\ frac {\ pi ^{2}} {12}} \ høyre]+O \ venstre ({\ frac {1} {\ Lambda ^{3}}} \ høyre) \ høyre \}}$	${\ displaystyle a}$: Wire radius : Lengde ${\ displaystyle \ ell}$ ${\ displaystyle \ Lambda = \ ln \ venstre (\ ell /a \ høyre)}$

Energilagring

Den energi (målt i Joule ) som er lagret i en kondensator er lik det arbeid som kreves for å presse ladningene i kondensatoren, det vil si for å lade den. Tenk på en kondensator med kapasitans C , som holder en ladning + q på den ene platen og - q på den andre. Å flytte et lite element av ladning d q fra den ene platen til den andre mot potensialforskjellen V = q/C krever arbeidet d W :

${\ displaystyle \ mathrm {d} W = {\ frac {q} {C}} \, \ mathrm {d} q}$

hvor W er arbeidet målt i joule, q er ladningen målt i coulombs og C er kapasitansen, målt i farads.

Energien lagret i en kondensator blir funnet ved å integrere denne ligningen. Starter med en uladet kapasitans ( q = 0 ) og flytter ladning fra den ene platen til den andre til platene har ladning + Q og - Q krever arbeidet W :

${\ displaystyle W _ {\ text {lading}} = \ int _ {0}^{Q} {\ frac {q} {C}} \, \ mathrm {d} q = {\ frac {1} {2} } {\ frac {Q^{2}} {C}} = {\ frac {1} {2}} QV = {\ frac {1} {2}} CV^{2} = W _ {\ text {lagret }}.}$

Nanoskala systemer

Kapasitansen til dielektriske kondensatorer i nanoskala, for eksempel kvantepunkter, kan avvike fra konvensjonelle formuleringer av større kondensatorer. Spesielt er den elektrostatiske potensialforskjellen som oppleves av elektroner i konvensjonelle kondensatorer romlig veldefinert og fikset av formen og størrelsen på metalliske elektroder i tillegg til det statistisk store antallet elektroner som er tilstede i konvensjonelle kondensatorer. I nanoskala kondensatorer bestemmes imidlertid de elektrostatiske potensialene som oppleves av elektroner av antallet og plasseringene til alle elektronene som bidrar til enhetens elektroniske egenskaper. I slike enheter kan antallet elektroner være veldig lite, så den resulterende romlige fordelingen av potensialflater i enheten er ekstremt kompleks.

Enkelte-elektroniske enheter

Kapasitansen til en tilkoblet, eller "lukket", enkelt-elektronenhet er to ganger kapasitansen til en ikke-tilkoblet, eller "åpen", enkelt-elektronenhet. Dette faktum kan spores mer fundamentalt til energien lagret i enkeltelektronenheten hvis "direkte polarisering" -interaksjonsenergi kan deles likt i elektronens interaksjon med den polariserte ladningen på selve enheten på grunn av tilstedeværelsen av elektronet og mengden potensiell energi som kreves for å danne den polariserte ladningen på enheten (vekselvirkning av ladninger i enhetens dielektriske materiale med potensialet på grunn av elektronet).

Få elektronenheter

Avledningen av en "kvantekapasitans" til noen få elektronenheter involverer det termodynamiske kjemiske potensialet til et N -partikkelsystem gitt av

${\ displaystyle \ mu (N) = U (N) -U (N-1)}$

hvis energibetingelser kan oppnås som løsninger av Schrödinger -ligningen. Definisjonen av kapasitans,

${\ displaystyle {1 \ over C} \ equiv {\ Delta \, V \ over \ Delta \, Q}}$,

med potensialforskjellen

${\ displaystyle \ Delta \, V = {\ Delta \, \ mu \, \ over e} = {\ mu (N+\ Delta \, N)-\ mu (N) \ over e}}$

kan påføres enheten med tillegg eller fjerning av individuelle elektroner,

${\ displaystyle \ Delta \, N = 1}$og .${\ displaystyle \ Delta \, Q = e}$

Deretter

${\ displaystyle C_ {Q} (N) = {e^{2} \ over \ mu (N+1)-\ mu (N)} = {e^{2} \ over E (N)}}$

er "kvantekapasitansen" til enheten.

Dette uttrykket for "kvantekapasitans" kan skrives som

${\ displaystyle C_ {Q} (N) = {e^{2} \ over U (N)}}$

som skiller seg fra det konvensjonelle uttrykket beskrevet i innledningen der den lagrede elektrostatiske potensielle energien, ${\ displaystyle W _ {\ text {lagret}} = U}$

${\ displaystyle C = {Q^{2} \ over 2U}}$

med en faktor 1/2 med . ${\ displaystyle Q = Ne}$

Men innenfor rammen av rent klassiske elektrostatiske interaksjoner er utseendet til faktoren 1/2 resultatet av integrering i den konvensjonelle formuleringen,

${\ displaystyle W _ {\ text {lading}} = U = \ int _ {0}^{Q} {\ frac {q} {C}} \, \ mathrm {d} q}$

som er hensiktsmessig ettersom for systemer som involverer enten mange elektroner eller av metallelektroder, men i noen-elektronsystemer, . Integralet blir vanligvis en summering. Man kan trivielt kombinere uttrykkene for kapasitans og elektrostatisk interaksjonsenergi, ${\ displaystyle \ mathrm {d} q = 0}$${\ displaystyle \ mathrm {d} q \ to \ Delta \, Q = e}$

${\ displaystyle Q = CV}$og ,${\ displaystyle U = QV}$

henholdsvis å få,

${\ displaystyle C = Q {1 \ over V} = Q {Q \ over U} = {Q^{2} \ over U}}$

som ligner kvantekapasitansen. En mer streng avledning er rapportert i litteraturen. Spesielt for å omgå de matematiske utfordringene til de romlig komplekse ekvipotensielle overflatene i enheten, brukes et gjennomsnittlig elektrostatisk potensial som hvert elektron opplever i avledningen.

Tilsynelatende matematiske forskjeller forstås mer fundamentalt som den potensielle energien til en isolert enhet (egenkapasitans) er dobbelt så stor som lagret i en "tilkoblet" enhet i den nedre grensen N = 1. Som N vokser store, . Dermed er det generelle uttrykket for kapasitans ${\ displaystyle U (N)}$${\ displaystyle U (N) \ til U}$

${\ displaystyle C (N) = {(Ne)^{2} \ over U (N)}}$.

I nanoskalaenheter som kvantepunkter er "kondensatoren" ofte en isolert eller delvis isolert komponent inne i enheten. De primære forskjellene mellom nanoskala kondensatorer og makroskopiske (konvensjonelle) kondensatorer er antall overflødige elektroner (ladningsbærere eller elektroner som bidrar til enhetens elektroniske oppførsel) og formen og størrelsen på metalliske elektroder. I nanoskalautstyr viser nanotråder som består av metallatomer vanligvis ikke de samme ledende egenskapene som deres makroskopiske eller bulkmaterialer.

Kapasitans i elektroniske og halvlederenheter

I elektroniske og halvlederenheter inneholder forbigående eller frekvensavhengig strøm mellom terminaler både lednings- og forskyvningskomponenter. Ledningsstrøm er relatert til ladbare bærere i bevegelse (elektroner, hull, ioner, etc.), mens forskyvningsstrøm er forårsaket av et tidsvarierende elektrisk felt. Bærertransport påvirkes av elektriske felt og av en rekke fysiske fenomener-som bærerdrift og diffusjon, fangst, injeksjon, kontaktrelaterte effekter, påvirkning ionisering, etc. Som et resultat er innrømmelse av enheter frekvensavhengig og enkel elektrostatisk formel for kapasitans er ikke aktuelt. En mer generell definisjon av kapasitans, som omfatter elektrostatisk formel, er: ${\ displaystyle C = q/V,}$

${\ displaystyle C = {\ frac {\ operatorname {Im} (Y (\ omega))} {\ omega}},}$

hvor er enhetens adgang, og er vinkelfrekvensen. ${\ displaystyle Y (\ omega)}$${\ displaystyle \ omega}$

Generelt er kapasitans en funksjon av frekvens. Ved høye frekvenser nærmer kapasitans seg en konstant verdi, lik "geometrisk" kapasitans, bestemt av terminalenes geometri og dielektriske innhold i enheten. Et papir av Steven Laux presenterer en gjennomgang av numeriske teknikker for kapasitansberegning. Spesielt kan kapasitans beregnes av en Fourier-transformasjon av en forbigående strøm som svar på en trinnlignende spenningseksitasjon:

${\ displaystyle C (\ omega) = 1/(\ Delta V) \ int _ {0}^{\ infty} [i (t) -i (\ infty)] \ cos (\ omega t) dt.}$

Negativ kapasitans i halvledere

Vanligvis er kapasitans i halvlederanordninger positiv. På noen enheter og under visse forhold (temperatur, påførte spenninger, frekvens, etc.) kan imidlertid kapasitans bli negativ. Ikke-monoton oppførsel av den forbigående strømmen som svar på en trinnlignende eksitasjon er blitt foreslått som mekanisme for negativ kapasitans. Negativ kapasitans har blitt demonstrert og utforsket i mange forskjellige typer halvledere.

Måling av kapasitans

En kapasitansmåler er et stykke elektronisk testutstyr som brukes til å måle kapasitans, hovedsakelig av diskrete kondensatorer . For de fleste formål og i de fleste tilfeller må kondensatoren kobles fra kretsen .

Mange DVM ( digitale voltmålere ) har en kapasitansmålefunksjon. Disse fungerer vanligvis ved å lade og tømme kondensatoren som testes med en kjent strøm og måle stigningshastigheten til den resulterende spenningen ; jo langsommere stigningshastighet, desto større kapasitans. DVM kan vanligvis måle kapasitans fra nanofarader til noen få hundre mikrofarader, men bredere områder er ikke uvanlige. Det er også mulig å måle kapasitans ved å føre en kjent høyfrekvent vekselstrøm gjennom enheten som testes og måle den resulterende spenningen over den (fungerer ikke for polariserte kondensatorer).

Mer sofistikerte instrumenter bruker andre teknikker som å sette kondensatoren under-test i en brokrets . Ved å variere verdiene til de andre beina i broen (for å bringe broen i balanse), bestemmes verdien av den ukjente kondensatoren. Denne metoden for indirekte bruk av målekapasitans sikrer større presisjon. Gjennom bruk av Kelvin -tilkoblinger og andre forsiktige designteknikker kan disse instrumentene vanligvis måle kondensatorer over et område fra picofarads til farads.

Se også

• Kapasitiv forskyvningssensor
• Kapasitet på et sett
• Quantum kapasitance
• Konduktans
• Forskyvningsstrøm
• Ampères sirkulasjonslov
• Gauss lov
• Hydraulisk analogi
• Magnetokapasitans
• RKM -kode
• LCR -måler

Referanser

Videre lesning