Koordinat nedstigning - Coordinate descent

Koordinat nedstigning er en optimaliseringsalgoritme som suksessivt minimerer langs koordinatretninger for å finne minimum av en funksjon. Ved hver iterasjon bestemmer algoritmen en koordinat- eller koordinatblokk via en koordinatseleksjonsregel, og minimerer deretter nøyaktig eller inexakt over det tilsvarende koordinathyperplanet mens alle andre koordinater eller koordinatblokker blir fikset. Et linjesøk langs koordinatretningen kan utføres ved gjeldende iterat for å bestemme riktig trinnstørrelse. Koordinert nedstigning er anvendelig i både differensierbare og derivatfrie sammenhenger.

Beskrivelse

Koordinert nedstigning er basert på ideen om at minimering av en multivariabel funksjon kan oppnås ved å minimere den langs en retning av gangen, dvs. løse univariate (eller i det minste mye enklere) optimaliseringsproblemer i en loop. I det enkleste tilfellet med syklisk koordinatnedstigning , går det syklisk gjennom retningene, en om gangen, og minimerer objektivfunksjonen med hensyn til hver koordinatretning om gangen. Det vil si å starte med innledende variabelverdier ${\ displaystyle F (\ mathbf {x})}$

${\ displaystyle \ mathbf {x}^{0} = (x_ {1}^{0}, \ ldots, x_ {n}^{0})}$,

runde definerer fra ved iterativt å løse problemene med optimalisering av enkeltvariabler ${\ displaystyle k+1}$${\ displaystyle \ mathbf {x} ^{k+1}}$${\ displaystyle \ mathbf {x} ^{k}}$

${\ displaystyle x_ {i}^{k+1} = {\ undersett {y \ in \ mathbb {R}} {\ operatorname {arg \, min}}} \; f (x_ {1}^{k+ 1}, \ dots, x_ {i-1}^{k+1}, y, x_ {i+1}^{k}, \ dots, x_ {n}^{k})}$

for hver variabel av , for fra 1 til . ${\ displaystyle x_ {i}}$${\ displaystyle \ mathbf {x}}$${\ displaystyle i}$${\ displaystyle n}$

Dermed begynner man med et innledende gjetning for et lokalt minimum på , og får en sekvens iterativt. ${\ displaystyle \ mathbf {x} ^{0}}$${\ displaystyle F}$${\ displaystyle \ mathbf {x} ^{0}, \ mathbf {x} ^{1}, \ mathbf {x} ^{2}, \ dots}$

Ved å gjøre linjesøk i hver iterasjon, har en automatisk

${\ displaystyle F (\ mathbf {x} ^{0}) \ geq F (\ mathbf {x} ^{1}) \ geq F (\ mathbf {x} ^{2}) \ geq \ dots.}$

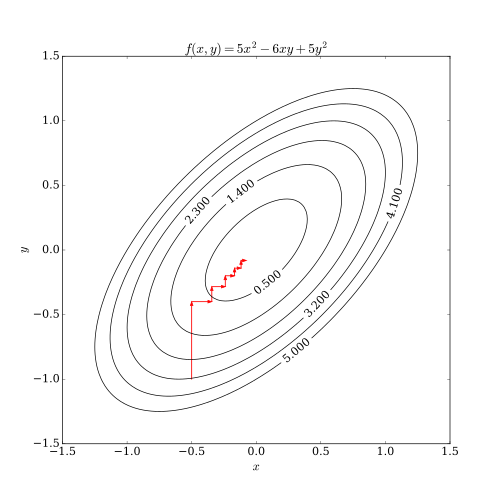
Det kan vises at denne sekvensen har lignende konvergensegenskaper som den bratteste nedstigningen. Ingen forbedring etter en syklus med linjesøk langs koordinatretninger innebærer at et stasjonært punkt er nådd.

Denne prosessen er illustrert nedenfor.

Differensierbar sak

I tilfelle av en kontinuerlig differensierbar funksjon F , kan en koordinat -nedstigningsalgoritme skisseres som:

Trinnstørrelsen kan velges på forskjellige måter, f.eks. Ved å løse den eksakte minimeren av f ( x _i ) = F ( x ) (dvs. F med alle variabler, men x _i fikset), eller ved tradisjonelle linjesøkskriterier.

Begrensninger

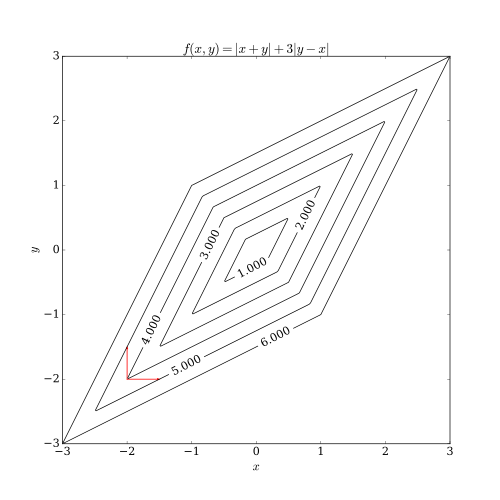
Koordinert nedstigning har to problemer. En av dem har en ikke- jevn multivariabel funksjon. Følgende bilde viser at koordinat-nedstigning iterasjon kan sette seg fast på et ikke- stasjonært punkt hvis nivåkurvene til en funksjon ikke er jevne. Anta at algoritmen er på punktet (-2, -2) ; så er det to aksejusterte retninger den kan vurdere for å ta et skritt, angitt med de røde pilene. Imidlertid vil hvert trinn langs disse to retningene øke objektfunksjonens verdi (forutsatt et minimeringsproblem), så algoritmen vil ikke ta noe skritt, selv om begge trinnene sammen vil bringe algoritmen nærmere det optimale. Selv om dette eksemplet viser at koordinatavstamning ikke nødvendigvis er konvergent til det optimale, er det mulig å vise formell konvergens under rimelige forhold.

Det andre problemet er vanskeligheter med parallellisme. Siden naturen til koordinatnedstigningen er å sykle gjennom retningene og minimere den objektive funksjonen med hensyn til hver koordinatretning, er ikke koordinatnedstigning en åpenbar kandidat for massiv parallellisme. Nyere forskningsarbeider har vist at massiv parallellisme er anvendelig for å koordinere nedstigning ved å slappe av endringen av objektivfunksjonen med hensyn til hver koordinatretning.

applikasjoner

Koordinere nedstigningsalgoritmer er populære blant utøvere på grunn av deres enkelhet, men den samme egenskapen har ført til at optimeringsforskere stort sett ignorerer dem til fordel for mer interessante (kompliserte) metoder. En tidlig anvendelse av optimalisering av koordinater for nedstigninger var innen computertomografi, der den har blitt funnet å ha rask konvergens og deretter ble brukt til klinisk multi-skive helisk skanning CT-rekonstruksjon. En syklisk koordinat -nedstigningsalgoritme (CCD) har blitt brukt i forutsigelse av proteinstruktur. I tillegg har det vært økende interesse for bruk av koordinat nedstigning med bruk av store problemer ved maskinlæring , hvor koordinaten nedstigning har vist seg konkurransedyktig med andre metoder når den brukes til slike problemer som trener lineære støttevektormaskiner (se LIBLINEAR ) og ikke-negativ matrisefaktorisering . De er attraktive for problemer der databehandlingsgradienter er umulige, kanskje fordi dataene som kreves for å gjøre det er distribuert over datanettverk.

Se også

• Adaptiv koordinat nedstigning
• Konjuger gradient
• Gradient nedstigning
• Linjesøk
• Matematisk optimalisering
• Newtons metode
• Stokastisk gradientnedstigning - bruker ett eksempel om gangen, i stedet for en koordinat

Referanser

• Bezdek, JC; Hathaway, RJ; Howard, RE; Wilson, CA; Windham, MP (1987), "Local convergence analysis of a grouped variable version of coordinate descent", Journal of Optimization Theory and Applications , Kluwer Academic/Plenum Publishers, 54 (3), s. 471–477, doi : 10.1007/BF00940196 , S2CID  120052975
• Bertsekas, Dimitri P. (1999). Ikke -lineær programmering, andre utgave Athena Scientific, Belmont, Massachusetts. ISBN  1-886529-00-0 .
• Luo, Zhiquan; Tseng, P. (1992), "On the convergence of the coordinate descent method for convex differentiable minimization", Journal of Optimization Theory and Applications , Kluwer Academic/Plenum Publishers, 72 (1), s. 7–35, doi : 10.1007 /BF00939948 , hdl : 1721.1/3164 , S2CID  121091844.
• Wu, TongTong; Lange, Kenneth (2008), "Coordinate descent algorithms for Lasso penalized regression", The Annals of Applied Statistics , Institute of Mathematical Statistics, 2 (1), s. 224–244, arXiv : 0803.3876 , doi : 10.1214/07-AOAS147 , S2CID  16350311.
• Richtarik, Peter; Takac, Martin (april 2011), "Iterasjonskompleksitet av randomiserte blokkoordinat-nedstigningsmetoder for å minimere en sammensatt funksjon", Mathematical Programming , Springer, 144 (1–2), s. 1–38, arXiv : 1107.2848 , doi : 10.1007 /s10107-012-0614-z , S2CID  16816638.
• Richtarik, Peter; Takac, Martin (desember 2012), "Parallel koordinere nedstigningen metoder for big data optimalisering", arxiv: 1212,0873 , arxiv : 1212,0873.