Grunnleggende par perioder - Fundamental pair of periods

I matematikk , en fundamental par perioder er et ordnet par av komplekse tall som definerer et gitter i det komplekse plan . Denne typen gitter er det underliggende objektet som elliptiske funksjoner og modulære former er definert med.

Selv om konseptet med et todimensjonalt gitter er ganske enkelt, er det en betydelig mengde spesialisert notasjon og språk angående gitteret som forekommer i matematisk litteratur. Denne artikkelen prøver å gjennomgå denne notasjonen, samt å presentere noen teoremer som er spesifikke for det todimensjonale tilfellet.

Grunnleggende parallellogram definert av et par vektorer i det komplekse planet.

Definisjon

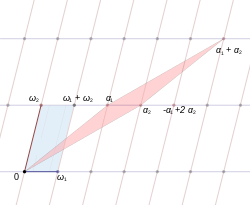
Et grunnleggende parpar er et par komplekse tall slik at forholdet ω ₂ /ω ₁ ikke er reelt. Med andre ord, betraktet som vektorer i , er de to ikke kollinære . Gitteret generert av ω ₁ og ω ₂ er ${\ displaystyle \ omega _ {1}, \ omega _ {2} \ in \ mathbb {C}}$${\ displaystyle \ mathbb {R} ^{2}}$

${\ displaystyle \ Lambda = \ left \ {m \ omega _ {1}+n \ omega _ {2} \ mid m, n \ in \ mathbb {Z} \ right \}}$

Dette gitteret er også noen ganger betegnet som Λ ( ω ₁ , ω ₂ ) for å tydeliggjøre at det avhenger av ω ₁ og ω ₂ . Det er også noen ganger merket med Ω eller Ω ( ω ₁ , ω ₂ ), eller rett og slett ved å ⟨ w ₁ , ω ₂ ⟩. De to generatorene ω ₁ og ω ₂ kalles gittergrunnlaget .

Den parallellogram definert av punktene 0, og kalles fundamental parallellogram . ${\ displaystyle \ omega _ {1}}$${\ displaystyle \ omega _ {2}}$

Det er viktig å merke seg at mens et grunnleggende par genererer et gitter, har et gitter ikke noe unikt grunnleggende par, det vil si at mange (faktisk et uendelig antall) grunnleggende par tilsvarer det samme gitteret.

Algebraiske egenskaper

Du kan se en rekke eiendommer nedenfor.

Ekvivalens

Et gitter som strekker seg over perioder ω ₁ og ω ₂ , som viser et ekvivalent par av perioder α ₁ og α ₂ .

To par av komplekse tall ( ω ₁ , co ₂ ) og (α ₁ , α ₂ ) kalles ekvivalente hvis de genererer det samme gitter: det vil si, hvis ⟨ω ₁ , ω ₂ ⟩ = ⟨α ₁ , α ₂ ⟩.

Ingen innvendige poeng

Det grunnleggende parallellogrammet inneholder ingen ytterligere gitterpunkter i sitt indre eller grense. Omvendt utgjør ethvert par gitterpunkter med denne egenskapen et grunnleggende par, og dessuten genererer de det samme gitteret.

Modulær symmetri

To par og er likeverdige hvis og bare hvis det finnes en 2 × 2 matrise med heltallsoppføringer a ,  b ,  c og  d og determinant ad - bc = ± 1 slik at ${\ displaystyle (\ omega _ {1}, \ omega _ {2})}$${\ displaystyle (\ alfa _ {1}, \ alpha _ {2})}$${\ displaystyle {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}}}$

${\ displaystyle {\ begin {pmatrix} \ alpha _ {1} \\\ alpha _ {2} \ end {pmatrix}} = {\ begin {pmatrix} a & b \\ c & d \ end {pmatrix}} {\ begin { pmatrix} \ omega _ {1} \\\ omega _ {2} \ end {pmatrix}},}$

det vil si så

${\ displaystyle \ alpha _ {1} = a \ omega _ {1}+b \ omega _ {2}}$

og

${\ displaystyle \ alpha _ {2} = c \ omega _ {1}+d \ omega _ {2}.}$

Legg merke til at denne matrisen hører til matrisen gruppe , som med liten misbruk av terminologi, er kjent som det modulære gruppen . Denne ekvivalensen til gitter kan tenkes å ligge til grunn for mange av egenskapene til elliptiske funksjoner (spesielt Weierstrass elliptiske funksjon ) og modulære former. ${\ displaystyle \ mathrm {SL} (2, \ mathbb {Z})}$

Topologiske egenskaper

Den abelske gruppen kartlegger det komplekse planet inn i det grunnleggende parallellogrammet. Det vil si at hvert punkt kan skrives som for heltall m , n , med et punkt p i det grunnleggende parallellogrammet. ${\ displaystyle \ mathbb {Z} ^{2}}$${\ displaystyle z \ in \ mathbb {C}}$${\ displaystyle z = p+m \ omega _ {1}+n \ omega _ {2}}$

Siden denne kartleggingen identifiserer motsatte sider av parallellogrammet som det samme, har det grunnleggende parallellogrammet topologien til en torus . Tilsvarende sier man at kvotmanifolden er en torus. ${\ displaystyle \ mathbb {C} /\ Lambda}$

Grunnleggende region

Det grå viser det kanoniske grunnleggende domenet.

Definer τ = ω ₂ / ω _{1 for} å være halvperioden . Da kan gittergrunnlaget alltid velges slik at τ ligger i en spesiell region, kalt det grunnleggende domenet . Alternativt eksisterer det alltid et element av PSL (2, Z ) som kartlegger et gittergrunnlag til et annet grunnlag slik at τ ligger i det grunnleggende domenet.

Det grunnleggende domenet er gitt av settet D , som består av et sett U pluss en del av grensen til U :

${\ displaystyle U = \ left \ {z \ in H: \ left | z \ right |> 1, \, \ left | \ operatorname {Re} (z) \ right | <{\ tfrac {1} {2} }\Ikke sant\}.}$

hvor H er det øvre halvplanet .

Det grunnleggende domenet D blir deretter bygget ved å legge til grensen til venstre pluss halve buen på bunnen:

${\ displaystyle D = U \ cup \ left \ {z \ in H: \ left | z \ right | \ geq 1, \, \ operatorname {Re} (z) =-{\ tfrac {1} {2}} \ right \} \ cup \ left \ {z \ in H: \ left | z \ right | = 1, \, \ operatorname {Re} (z) \ leq 0 \ right \}.}$

Tre saker gjelder:

• Hvis og , så er det nøyaktig to gitterbaser med samme τ i den grunnleggende regionen: og${\ displaystyle \ tau \ neq i}$${\ displaystyle \ tau \ neq e^{{\ frac {1} {3}} i \ pi}}$${\ displaystyle (\ omega _ {1}, \ omega _ {2})}$${\ displaystyle (-\ omega _ {1},-\ omega _ {2}).}$
• Hvis , så har fire gitterbaser samme τ: to ovenfor , og ,${\ displaystyle \ tau = i}$${\ displaystyle (\ omega _ {1}, \ omega _ {2})}$${\ displaystyle (-\ omega _ {1},-\ omega _ {2})}$${\ displaystyle (i \ omega _ {1}, i \ omega _ {2})}$${\ displaystyle (-i \ omega _ {1},-i \ omega _ {2}).}$
• Hvis , så er det seks gitter baser med den samme τ: , , og deres negativer.${\ displaystyle \ tau = e^{{\ frac {1} {3}} i \ pi}}$${\ displaystyle (\ omega _ {1}, \ omega _ {2})}$${\ displaystyle (\ tau \ omega _ {1}, \ tau \ omega _ {2})}$${\ displaystyle (\ tau ^{2} \ omega _ {1}, \ tau ^{2} \ omega _ {2})}$

Vær oppmerksom på at i avslutningen av det grunnleggende domenet: og${\ displaystyle \ tau = i}$${\ displaystyle \ tau = e^{{\ frac {1} {3}} i \ pi}.}$

Se også

• En rekke alternative notasjoner for gitteret og for det grunnleggende paret eksisterer, og brukes ofte i stedet. Se for eksempel artiklene om nomen , elliptisk modul , kvartalsperiode og halvperiode .
• Elliptisk kurve
• Modulær form
• Eisenstein -serien

Referanser

• Tom M. Apostol , Modular functions and Dirichlet Series in Number Theory (1990), Springer-Verlag, New York. ISBN  0-387-97127-0 (Se kapittel 1 og 2.)
• Jurgen Jost, Compact Riemann Surfaces (2002), Springer-Verlag, New York. ISBN  3-540-43299-X (Se kapittel 2.)