Lineær regresjon - Linear regression
| Del av en serie om |
| Regresjonsanalyse |
|---|
| Modeller |
| Anslag |
| Bakgrunn |
I statistikk er lineær regresjon en lineær tilnærming for å modellere forholdet mellom en skalarrespons og en eller flere forklarende variabler (også kjent som avhengige og uavhengige variabler ). Tilfellet med en forklarende variabel kalles enkel lineær regresjon ; for mer enn én kalles prosessen multiple lineær regresjon . Dette begrepet skiller seg fra multivariat lineær regresjon , hvor flere korrelerte avhengige variabler forutsies, snarere enn en enkelt skalarvariabel.
Ved lineær regresjon modelleres relasjonene ved hjelp av lineære prediktorfunksjoner hvis ukjente modellparametere er estimert ut fra dataene . Slike modeller kalles lineære modeller . Vanligvis antas det betingede gjennomsnittet av responset gitt verdiene til de forklarende variablene (eller prediktorene) å være en affin funksjon av disse verdiene; mindre vanlig brukes den betingede medianen eller en annen kvantil . Som alle former for regresjonsanalyse fokuserer lineær regresjon på den betingede sannsynlighetsfordelingen av responset gitt verdiene til prediktorene, snarere enn på den felles sannsynlighetsfordelingen for alle disse variablene, som er domenet til multivariat analyse .
Lineær regresjon var den første typen regresjonsanalyse som ble studert grundig, og som ble brukt mye i praktiske applikasjoner. Dette er fordi modeller som er lineært avhengig av deres ukjente parametere er lettere å montere enn modeller som er ikke-lineært relatert til parametrene, og fordi de statistiske egenskapene til de resulterende estimatorene er lettere å bestemme.
Lineær regresjon har mange praktiske bruksområder. De fleste applikasjoner faller inn i en av følgende to brede kategorier:
- Hvis målet er prediksjon , prognose eller feilreduksjon, kan lineær regresjon brukes for å tilpasse en prediktiv modell til et observert datasett med verdier for responsen og forklaringsvariabler. Etter å ha utviklet en slik modell, hvis tilleggsverdier av de forklarende variablene samles inn uten en tilhørende responsverdi, kan den tilpassede modellen brukes til å forutsi responsen.
- Hvis målet er å forklare variasjon i responsvariabelen som kan tilskrives variasjon i forklaringsvariablene, kan lineær regresjonsanalyse brukes for å kvantifisere styrken til forholdet mellom responsen og de forklarende variablene, og spesielt for å avgjøre om noen forklarende variabler har kanskje ikke noe lineært forhold til responsen i det hele tatt, eller for å identifisere hvilke undersett av forklarende variabler som kan inneholde overflødig informasjon om responsen.
Lineære regresjonsmodeller blir ofte montert ved hjelp av tilnærmingen med minst kvadrater , men de kan også monteres på andre måter, for eksempel ved å minimere "mangel på passform" i en annen norm (som med minst absolutt avviksregresjon), eller ved å minimere en straffet versjon av de minste kvadratene koster funksjon som ved møne -regresjon ( L 2 -norm straff) og lasso ( L 1 -normal straff). Motsatt kan tilnærmingen med minst kvadrater brukes til å passe modeller som ikke er lineære modeller. Selv om begrepene "minst kvadrater" og "lineær modell" er nært knyttet sammen, er de således ikke synonyme.
Formulering
Gitt et datasettet av n statistiske enheter , forutsetter en lineær regresjonsmodell at forholdet mellom den avhengige variable y og p -vector av regressors x er lineær . Dette forholdet er modellert gjennom en forstyrrelsesbetegnelse eller feilvariabel ε - en ikke -observert tilfeldig variabel som tilfører "støy" til det lineære forholdet mellom den avhengige variabelen og regressorene. Dermed tar modellen form
hvor T betegner transponeringen , slik at x i T β er det indre produktet mellom vektorene x i og β .
Ofte er disse n ligningene stablet sammen og skrevet i matrisenotasjon som
hvor
Notasjon og terminologi
- er en vektor med observerte verdier av variabelen kalt regressand , endogen variabel , responsvariabel , målt variabel , kriterievariabel eller avhengig variabel . Denne variabelen er også noen ganger kjent som den forutsagte variabelen , men dette bør ikke forveksles med forutsagte verdier , som er angitt . Beslutningen om hvilken variabel i et datasett som er modellert som den avhengige variabelen og som er modellert som de uavhengige variablene, kan være basert på en antagelse om at verdien av en av variablene er forårsaket av eller direkte påvirket av de andre variablene. Alternativt kan det være en operasjonell grunn til å modellere en av variablene når det gjelder de andre, i så fall trenger det ikke være noen formodning om årsakssammenheng.
-
kan sees på som en matrise av radvektorer eller av n- dimensjonale kolonnevektorer , som er kjent som regressorer , eksogene variabler , forklarende variabler , kovariater , inputvariabler , prediktorvariabler eller uavhengige variabler (ikke å forveksle med konseptet av uavhengige tilfeldige variabler ). Matrisen kalles noen ganger designmatrisen .
- Vanligvis er en konstant inkludert som en av regressorene. Spesielt for . Det tilsvarende elementet i
- Noen ganger kan en av regressorene være en ikke-lineær funksjon av en annen regressor eller av dataene, som i polynomregresjon og segmentert regresjon . Modellen forblir lineær så lenge den er lineær i parametervektoren β .
- Verdiene x ij kan sees på som enten observerte verdier for tilfeldige variabler X j eller som faste verdier valgt før man observerer den avhengige variabelen. Begge tolkningene kan være passende i forskjellige tilfeller, og de fører vanligvis til de samme estimeringsprosedyrene; Imidlertid brukes forskjellige tilnærminger til asymptotisk analyse i disse to situasjonene.
Å tilpasse en lineær modell til et gitt datasett krever vanligvis estimering av regresjonskoeffisientene slik at feilbegrepet minimeres. For eksempel er det vanlig å bruke summen av kvadratiske feil som et mål for minimering.
Eksempel
Betrakt en situasjon der en liten ball som blir kastet opp i luften og deretter vi måler sine høyder av oppstigningen h jeg på ulike momenter i tid t jeg . Fysikk forteller oss at forholdet kan modelleres som om man ignorerer trekket
der β 1 bestemmer ballens starthastighet, β 2 er proporsjonal med standard tyngdekraften , og ε i skyldes målefeil. Lineær regresjon kan brukes til å estimere verdiene av β 1 og β 2 fra de målte dataene. Denne modellen er ikke-lineær i tidsvariabelen, men den er lineær i parameterne β 1 og β 2 ; hvis vi tar regressorer x i = ( x i 1 , x i 2 ) = ( t i , t i 2 ), tar modellen standardformen
Antagelser
Standard lineære regresjonsmodeller med standard estimeringsteknikker gjør en rekke forutsetninger om prediktorvariablene, responsvariablene og deres forhold. Det er utviklet mange utvidelser som gjør at hver av disse forutsetningene kan lempes (dvs. reduseres til en svakere form), og i noen tilfeller elimineres helt. Vanligvis gjør disse utvidelsene estimeringsprosedyren mer kompleks og tidkrevende, og kan også kreve flere data for å produsere en like presis modell.
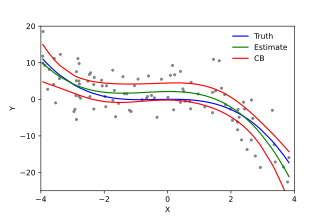
Følgende er de viktigste forutsetningene fra standard lineære regresjonsmodeller med standard estimeringsteknikker (f.eks. Vanlige minste kvadrater ):
- Svak eksogenitet . Dette betyr i hovedsak at prediktorvariablene x kan behandles som faste verdier, i stedet for tilfeldige variabler . Dette betyr for eksempel at prediktorvariablene antas å være feilfrie-det vil si at de ikke er forurenset med målefeil. Selv om denne antagelsen ikke er realistisk i mange innstillinger, fører det til at det å slippe den til betydelig vanskeligere modeller med feil-i-variabler .
- Linjæritet . Dette betyr at gjennomsnittet av responsvariabelen er en lineær kombinasjon av parameterne (regresjonskoeffisienter) og prediktorvariablene. Vær oppmerksom på at denne antagelsen er mye mindre restriktiv enn den kan se ut til å begynne med. Fordi prediktorvariablene behandles som faste verdier (se ovenfor), er linearitet egentlig bare en begrensning på parametrene. Selve prediktorvariablene kan transformeres vilkårlig, og faktisk kan flere kopier av den samme underliggende prediktorvariabelen legges til, hver enkelt transformert annerledes. Denne teknikken brukes for eksempel i polynomregresjon , som bruker lineær regresjon for å passe responsvariabelen som en vilkårlig polynomfunksjon (opptil en gitt rangering) av en prediktorvariabel. Med denne store fleksibiliteten har modeller som polynomisk regresjon ofte "for mye makt", ved at de har en tendens til å overpasse dataene. Som et resultat må en typisk regularisering vanligvis brukes for å forhindre at urimelige løsninger kommer ut av estimeringsprosessen. Vanlige eksempler er åsregresjon og lassoregresjon . Bayesisk lineær regresjon kan også brukes, som av sin natur er mer eller mindre immun mot problemet med overmontering. (Faktisk kan ryggeregresjon og lasso -regresjon begge sees på som spesielle tilfeller av Bayesian lineær regresjon, med bestemte typer tidligere fordelinger plassert på regresjonskoeffisientene.)
- Konstant varians (aka homoscedasticity ). Dette betyr at variansen til feilene ikke er avhengig av verdiene til prediktorvariablene. Således er variasjonen i responsene for gitte faste verdier for prediktorene den samme uavhengig av hvor store eller små responsene er. Dette er ofte ikke tilfelle, ettersom en variabel hvis gjennomsnitt er stort vanligvis vil ha en større varians enn en hvis gjennomsnitt er liten. For eksempel kan en person hvis inntekt er spådd til å være $ 100 000 lett ha en faktisk inntekt på $ 80 000 eller $ 120 000 - det vil si et standardavvik på rundt $ 20 000 - mens en annen person med en forutsagt inntekt på $ 10 000 usannsynlig vil ha samme standardavvik på $ 20 000 , siden det ville innebære at deres faktiske inntekt kan variere mellom - $ 10.000 og $ 30.000. (Faktisk, som dette viser, i mange tilfeller - ofte de samme tilfellene hvor antagelsen om normalfordelte feil mislykkes - bør variansen eller standardavviket forutsies å være proporsjonal med gjennomsnittet, snarere enn konstant.) Fraværet av homoscedasticitet er kalles heteroscedasticitet . For å kontrollere denne antagelsen, kan et plott av residualer versus forutsagte verdier (eller verdiene til hver individuelle prediktor) undersøkes for en "viftende effekt" (dvs. økende eller redusert vertikal spredning når man beveger seg fra venstre til høyre på plottet) . Et plott av de absolutte eller kvadratiske residualene versus de forutsagte verdiene (eller hver prediktor) kan også undersøkes for en trend eller krumning. Formelle tester kan også brukes; se heteroscedasticitet . Tilstedeværelsen av heteroscedasticitet vil resultere i at et generelt "gjennomsnittlig" estimat av varians blir brukt i stedet for et som tar hensyn til den sanne variansestrukturen. Dette fører til mindre presise (men i tilfelle vanlige minst kvadrater , ikke partiske) parameterestimater og partiske standardfeil, noe som resulterer i villedende tester og intervallestimater. Den gjennomsnittlige kvadratfeilen for modellen vil også være feil. Ulike estimeringsteknikker, inkludert vektede minste kvadrater og bruk av heteroscedasticitet-konsistente standardfeil, kan håndtere heteroscedasticitet på en ganske generell måte. Bayesiske lineære regresjonsteknikker kan også brukes når variansen antas å være en funksjon av gjennomsnittet. Det er også mulig i noen tilfeller å fikse problemet ved å bruke en transformasjon på responsvariabelen (f.eks. Tilpasning av logaritmen til responsvariabelen ved hjelp av en lineær regresjonsmodell, noe som innebærer at responsvariabelen selv har en log-normalfordeling i stedet for en normal fordeling ).
-
Uavhengighet av feil . Dette forutsetter at feilene i responsvariablene er ukorrelerte med hverandre. (Faktisk statistisk uavhengighet er en sterkere betingelse enn mangel på korrelasjon og er ofte ikke nødvendig, selv om den kan utnyttes hvis den er kjent for å holde.) Noen metoder som generaliserte minste kvadrater er i stand til å håndtere korrelerte feil, selv om de vanligvis krever betydelig flere data med mindre en form for regularisering brukes for å forutse modellen mot å anta ukorrelerte feil. Bayesisk lineær regresjon er en generell måte å håndtere dette problemet på.
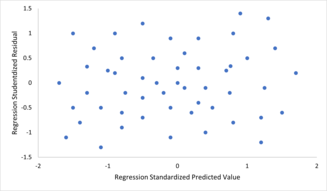 For å se etter brudd på forutsetningene om linearitet, konstant varians og uavhengighet av feil i en lineær regresjonsmodell, blir residualene vanligvis plottet opp mot de forutsagte verdiene (eller hver av de individuelle prediktorene). En tilsynelatende tilfeldig spredning av punkter om den horisontale midtlinjen på 0 er ideell, men kan ikke utelukke visse typer brudd som autokorrelasjon i feilene eller deres korrelasjon med ett eller flere kovariater.
For å se etter brudd på forutsetningene om linearitet, konstant varians og uavhengighet av feil i en lineær regresjonsmodell, blir residualene vanligvis plottet opp mot de forutsagte verdiene (eller hver av de individuelle prediktorene). En tilsynelatende tilfeldig spredning av punkter om den horisontale midtlinjen på 0 er ideell, men kan ikke utelukke visse typer brudd som autokorrelasjon i feilene eller deres korrelasjon med ett eller flere kovariater. - Mangel på perfekt multikollinearitet i prediktorene. For standardmetoder for estimering av minst kvadrater må designmatrisen X ha full kolonne rangering p ; ellers eksisterer perfekt multikollinearitet i prediktorvariablene, noe som betyr at det eksisterer et lineært forhold mellom to eller flere prediktorvariabler. Dette kan skyldes at du ved et uhell dupliserer en variabel i dataene, bruker en lineær transformasjon av en variabel sammen med originalen (f.eks. De samme temperaturmålingene uttrykt i Fahrenheit og Celsius), eller inkluderer en lineær kombinasjon av flere variabler i modellen, som deres gjennomsnitt. Det kan også skje hvis det er for lite data tilgjengelig sammenlignet med antall parametere som skal estimeres (f.eks. Færre datapunkter enn regresjonskoeffisienter). Nær brudd på denne antagelsen, hvor prediktorer er sterkt, men ikke perfekt korrelert, kan redusere presisjonen til parameterestimater (se Variansinflasjonsfaktor ). Ved perfekt multikollinearitet vil parametervektoren β være ikke identifiserbar-den har ingen unik løsning. I et slikt tilfelle, bare noen av parametrene kan bli identifisert (dvs. deres verdier kan bare anslås innenfor noen lineære underrom av hele parameterrommet R p ). Se delvis minste kvadraters regresjon . Metoder for montering av lineære modeller med multikollinearitet er utviklet, hvorav noen krever ytterligere forutsetninger som "effektsparsitet" - at en stor brøkdel av effektene er nøyaktig null. Vær oppmerksom på at de mer beregningsmessig dyre itererte algoritmene for parameterestimering, slik som de som brukes i generaliserte lineære modeller , ikke lider av dette problemet.
Utover disse forutsetningene påvirker flere andre statistiske egenskaper av dataene sterkt ytelsen til forskjellige estimeringsmetoder:
- Det statistiske forholdet mellom feilbetingelsene og regressorene spiller en viktig rolle for å avgjøre om en estimeringsprosedyre har ønskelige prøvetakingsegenskaper, for eksempel å være upartisk og konsistent.
- Arrangementet eller sannsynlighetsfordelingen til prediktorvariablene x har stor innflytelse på presisjonen av estimater av β . Prøvetaking og design av eksperimenter er høyt utviklede underfelt med statistikk som gir veiledning for innsamling av data på en slik måte at man oppnår et presist estimat av β .
Tolkning

En montert lineær regresjonsmodell kan brukes til å identifisere forholdet mellom en enkelt prediktorvariabel x j og responsvariabelen y når alle de andre prediktorvariablene i modellen "holdes faste". Spesielt er tolkningen av β j den forventede endringen i y for en enhetsendring i x j når de andre kovariatene holdes faste-det vil si den forventede verdien av det partielle derivatet av y med hensyn til x j . Dette kalles noen ganger den unike effekten av x j på y . I kontrast kan marginaleffekten av x j på y vurderes ved hjelp av en korrelasjonskoeffisient eller enkel lineær regresjonsmodell som bare relaterer x j til y ; denne effekten er det totale derivatet av y med hensyn til x j .
Det må utvises forsiktighet ved tolkning av regresjonsresultater, ettersom noen av regressorene kanskje ikke tillater marginale endringer (for eksempel dummy -variabler eller avskjæringsbegrepet), mens andre ikke kan holdes fast (husk eksemplet fra innledningen: det ville være umulig å "holde t i fast" og samtidig endre verdien av t i 2 ).
Det er mulig at den unike effekten kan være nesten null, selv når marginaleffekten er stor. Dette kan antyde at noen andre kovariater fanger all informasjon i x j , slik at når variabelen først er i modellen, er det ikke noe bidrag fra x j til variasjonen i y . Motsatt kan den unike effekten av x j være stor mens dens marginale effekt er nesten null. Dette ville skje hvis de andre kovariatene forklarte mye av variasjonen av y , men de forklarer hovedsakelig variasjon på en måte som er komplementær til det som fanges opp av x j . I dette tilfellet reduserer inkluderingen av de andre variablene i modellen den delen av variabiliteten til y som ikke er relatert til x j , og styrker dermed det tilsynelatende forholdet til x j .
Betydningen av uttrykket "holdt fast" kan avhenge av hvordan verdiene til prediktorvariablene oppstår. Hvis eksperimentatoren direkte setter verdiene til prediktorvariablene i henhold til en studiedesign, kan sammenligningene av interesse bokstavelig talt svare til sammenligninger mellom enheter hvis prediktorvariabler har blitt "holdt fast" av eksperimentatoren. Alternativt kan uttrykket "holdt fast" referere til et utvalg som finner sted i sammenheng med dataanalyse. I dette tilfellet "holder vi en variabel fast" ved å begrense vår oppmerksomhet til undersettene til dataene som tilfeldigvis har en felles verdi for den gitte prediktorvariabelen. Dette er den eneste tolkningen av "holdt fast" som kan brukes i en observasjonsstudie.
Forestillingen om en "unik effekt" er tiltalende når man studerer et komplekst system der flere sammenhengende komponenter påvirker responsvariabelen. I noen tilfeller kan det bokstavelig talt tolkes som årsakseffekten av et inngrep som er knyttet til verdien av en prediktorvariabel. Imidlertid har det blitt hevdet at i mange tilfeller mislykkes multiple regresjonsanalyser for å klargjøre forholdet mellom prediktorvariablene og responsvariabelen når prediktorene er korrelert med hverandre og ikke blir tildelt etter en studiedesign.
Utvidelser
Det er utviklet en rekke utvidelser av lineær regresjon, som gjør at noen eller alle forutsetningene som ligger til grunn for grunnmodellen, kan lempes.
Enkel og multiple lineær regresjon

Den aller enkleste tilfelle med en enkel skalar prediktor variable x og en enkelt skalar responsvariabelen Y er kjent som enkel lineær regresjon . Utvidelsen til flere og/eller vektorverdierte prediktorvariabler (betegnet med store X ) er kjent som multiple lineær regresjon , også kjent som multivariabel lineær regresjon (ikke å forveksle med multivariat lineær regresjon ).
Multipel lineær regresjon er en generalisering av enkel lineær regresjon til tilfellet med mer enn en uavhengig variabel, og et spesielt tilfelle av generelle lineære modeller, begrenset til en avhengig variabel. Den grunnleggende modellen for multipel lineær regresjon er
for hver observasjon i = 1, ..., n .
I formelen ovenfor vurderer vi n observasjoner av en avhengig variabel og p uavhengige variabler. Således Y i er den i th observasjon av den avhengige variable, X ij er i th observasjon av j th uavhengige variabelen, j = 1, 2, ..., p . Verdiene p j representerer parametrene som skal estimeres, og iU ^ i er den i th uavhengig identisk fordelt normale feilen.
I den mer generelle multivariate lineære regresjonen er det en ligning av skjemaet ovenfor for hver av m > 1 avhengige variabler som deler det samme settet med forklarende variabler og derfor estimeres samtidig med hverandre:
for alle observasjoner indeksert som i = 1, ..., n og for alle avhengige variabler indeksert som j = 1, ..., m .
Nesten alle regresjonsmodeller fra den virkelige verden involverer flere prediktorer, og grunnleggende beskrivelser av lineær regresjon er ofte formulert i form av multiple regresjonsmodellen. Vær imidlertid oppmerksom på at responsvariabelen y i disse tilfellene fortsatt er en skalar. Et annet begrep, multivariat lineær regresjon , refererer til tilfeller der y er en vektor, dvs. det samme som generell lineær regresjon .
Generelle lineære modeller
Den generelle lineære modellen vurderer situasjonen når responsvariabelen ikke er en skalar (for hver observasjon), men en vektor, y i . Det er fortsatt antatt betinget linearitet med en matrise B som erstatter vektoren β i den klassiske lineære regresjonsmodellen. Multivariate analoger av vanlige minste kvadrater (OLS) og generaliserte minste kvadrater (GLS) er utviklet. "Generelle lineære modeller" kalles også "multivariate lineære modeller". Disse er ikke det samme som multivariable lineære modeller (også kalt "multiple lineære modeller").
Heteroscedastiske modeller
Det er laget forskjellige modeller som åpner for heteroscedasticitet , dvs. at feilene for forskjellige responsvariabler kan ha forskjellige avvik . For eksempel er veide minste kvadrater en metode for å estimere lineære regresjonsmodeller når responsvariablene kan ha forskjellige feilavvik, muligens med korrelerte feil. (Se også Vektede lineære minste kvadrater og Generaliserte minst kvadrater .) Heteroscedasticitetskonsistente standardfeil er en forbedret metode for bruk med ukorrelerte, men potensielt heteroscedastiske feil.
Generaliserte lineære modeller
Generaliserte lineære modeller (GLM) er et rammeverk for modellering av responsvariabler som er begrenset eller diskret. Dette brukes, for eksempel:
- ved modellering av positive mengder (f.eks. priser eller populasjoner) som varierer i stor skala-som beskrives bedre ved hjelp av en skjev fordeling som log-normalfordelingen eller Poisson-fordelingen (selv om GLM-er ikke brukes til loggnormale data, i stedet svaret variabel blir ganske enkelt transformert ved hjelp av logaritmefunksjonen);
- ved modellering av kategoriske data , for eksempel valg av en gitt kandidat i et valg (som er bedre beskrevet ved bruk av en Bernoulli-fordeling / binomial fordeling for binære valg, eller en kategorisk fordeling / multinomial fordeling for flerveisvalg), hvor det er en fast antall valg som ikke kan ordnes meningsfullt;
- ved modellering av ordinære data , f.eks. rangeringer på en skala fra 0 til 5, der de forskjellige utfallene kan bestilles, men hvor mengden i seg selv kanskje ikke har noen absolutt betydning (f.eks. kan en vurdering på 4 ikke være "dobbelt så god" i noe mål forstand som en vurdering på 2, men indikerer ganske enkelt at den er bedre enn 2 eller 3, men ikke så god som 5).
Generaliserte lineære modeller gir mulighet for en vilkårlig kobling funksjon , g , som angår den midlere av responsvariabelen (e) til prediktorene: . Lenkefunksjonen er ofte relatert til fordelingen av responsen, og spesielt har den vanligvis effekten av å transformere mellom området til den lineære prediktoren og området til responsvariabelen.
Noen vanlige eksempler på GLM er:
- Poisson -regresjon for telledata.
- Logistisk regresjon og probitregresjon for binære data.
- Multinom logistisk regresjon og multinom probit regresjon for kategoriske data.
- Bestilte logit og bestilte probit -regresjon for ordinære data.
Enkeltindeksmodeller tillater en viss grad av ikke -linearitet i forholdet mellom x og y , samtidig som den sentrale rollen til den lineære prediktoren β ′ x beholdes som i den klassiske lineære regresjonsmodellen. Under visse forhold vil ganske enkelt å bruke OLS på data fra en enkeltindeksmodell konsekvent estimere β opp til en proporsjonalitetskonstant.
Hierarkiske lineære modeller
Hierarkiske lineære modeller (eller flere nivåer regresjon ) organiserer dataene i et hierarki av regresjoner, for eksempel hvor A er gått tilbake på B , og B er gått tilbake på C . Det brukes ofte der variablene av interesse har en naturlig hierarkisk struktur, for eksempel i utdanningsstatistikk, der elevene er hekkende i klasserom, klasserom er hekket på skoler, og skoler er nestet i en administrativ gruppering, for eksempel et skoledistrikt. Svarvariabelen kan være et mål på elevprestasjoner, for eksempel en testscore, og forskjellige kovariater vil bli samlet på klasseroms-, skole- og skoledistriktnivå.
Feil-i-variabler
Modeller med feil i variabler (eller "målefeilmodeller") utvider den tradisjonelle lineære regresjonsmodellen slik at prediktorvariablene X kan observeres med feil. Denne feilen fører til at standardestimatorer av β blir partiske. Generelt er skjevheten en demping, noe som betyr at effektene er forspent mot null.
Andre
- I Dempster - Shafer -teorien , eller en lineær trosfunksjon spesielt, kan en lineær regresjonsmodell bli representert som en delvis feid matrise, som kan kombineres med lignende matriser som representerer observasjoner og andre antatte normalfordelinger og tilstandsligninger. Kombinasjonen av feide eller ikke -feide matriser gir en alternativ metode for å estimere lineære regresjonsmodeller.
Estimeringsmetoder
Et stort antall prosedyrer er utviklet for parameterestimering og slutning ved lineær regresjon. Disse metodene er forskjellige i beregningsmessig enkelhet av algoritmer, tilstedeværelse av en lukket formløsning, robusthet med hensyn til kraftige fordelinger og teoretiske forutsetninger som trengs for å validere ønskelige statistiske egenskaper som konsistens og asymptotisk effektivitet .
Noen av de mer vanlige estimeringsteknikkene for lineær regresjon er oppsummert nedenfor.
Forutsatt at den uavhengige variabelen er og modellens parametere er , vil modellens prediksjon være
- .
Hvis utvides til da ville bli et prikkprodukt av parameteren og den uavhengige variabelen, dvs.
- .
I innstillingen med minst kvadrater er den optimale parameteren definert slik at den minimerer summen av gjennomsnittlig kvadrat tap:
Når du setter de uavhengige og avhengige variablene i henholdsvis matriser og tap, kan tapsfunksjonen skrives om til:
Siden tapet er konveks, ligger den optimale løsningen ved gradient null. Gradienten til tapsfunksjonen er (ved hjelp av nevneroppsettskonvensjon ):
Å sette gradienten til null gir den optimale parameteren:
Merk: For å bevise at det oppnådde faktisk er det lokale minimumet, må man differensiere nok en gang for å få den hessiske matrisen og vise at den er positiv bestemt. Dette er gitt av Gauss - Markov -teoremet .
Lineære minste kvadratmetoder inkluderer hovedsakelig:
- Maksimal sannsynlighetsestimering kan utføres når fordelingen av feilbetingelsene er kjent for å tilhøre en bestemt parametrisk familie ƒ θ av sannsynlighetsfordelinger . Når f θ er en normalfordeling med null gjennomsnitt og varians θ, er det resulterende estimatet identisk med OLS -estimatet. GLS -estimater er maksimale sannsynlighetsestimater når ε følger en multivariat normalfordeling med en kjent kovariansematrise .
- Åsregresjon og andre former for straffet estimering, for eksempel Lasso -regresjon , introduserer bevisst skjevhet i estimeringen av β for å redusereestimatets variabilitet . De resulterende estimatene har vanligvis lavere gjennomsnittlig kvadratfeil enn OLS -estimatene, spesielt når multikollinearitet er tilstede eller når overmontering er et problem. De brukes vanligvis når målet er å forutsi verdien av responsvariabelen y for verdier av prediktorene x som ennå ikke er observert. Disse metodene er ikke like vanlig når målet er slutning, siden det er vanskelig å ta høyde for skjevheten.
- Minst absolutt avvik (LAD) regresjon er en robust estimeringsteknikk ved at den er mindre følsom for tilstedeværelsen av utfall enn OLS (men er mindre effektiv enn OLS når ingen avvik er tilstede). Det tilsvarer maksimal sannsynlighetsestimering under en Laplace -distribusjonsmodell for ε .
- Adaptiv estimering . Hvis vi antar at feiltermer er uavhengige av regressorene, så er den optimale estimatoren 2-trinns MLE, der det første trinnet brukes til å estimere fordelingen av feilbegrepet ikke-parametrisk.
Andre estimeringsteknikker

- Bayesisk lineær regresjon bruker rammeverket for bayesiansk statistikk for lineær regresjon. (Se også Bayesian multivariat lineær regresjon .) Spesielt antas regresjonskoeffisientene β å være tilfeldige variabler med en spesifisert tidligere fordeling . Den tidligere fordelingen kan forstyrre løsningene for regresjonskoeffisientene, på en måte som ligner på (men mer generell enn) ryggenes regresjon eller lasso -regresjon . I tillegg produserer den bayesiske estimeringsprosessen ikke et eneste punktestimat for de "beste" verdiene til regresjonskoeffisientene, men en hel posterior fordeling , som beskriver usikkerheten rundt mengden fullstendig. Dette kan brukes til å estimere de "beste" koeffisientene ved å bruke gjennomsnittet, modusen, medianen, hvilken som helst kvantil (se kvantil regresjon ) eller en hvilken som helst annen funksjon av den bakre fordelingen.
- Quantile regresjon fokuserer på de betingede quantiles av y gitt X i stedet for den betingede gjennomsnittet av y gitt X . Lineær kvantil regresjon modellerer en bestemt betinget kvantil, for eksempel betinget median, som en lineær funksjon β T x for prediktorene.
- Blandede modeller er mye brukt for å analysere lineære regresjonsforhold som involverer avhengige data når avhengighetene har en kjent struktur. Vanlige anvendelser av blandede modeller inkluderer analyse av data som involverer gjentatte målinger, for eksempel langsgående data, eller data hentet fra klyngeprøvetaking. De passer generelt som parametriske modeller, ved å bruke maksimal sannsynlighet eller Bayesiansk estimering. I tilfellet der feilene er modellert som normale tilfeldige variabler, er det en nær forbindelse mellom blandede modeller og generaliserte minst kvadrater. Estimering av faste effekter er en alternativ tilnærming til å analysere denne typen data.
- Hovedkomponentregresjon (PCR) brukes når antallet prediktorvariabler er stort, eller når det finnes sterke korrelasjoner blant prediktorvariablene. Denne to-trinns prosedyren reduserer først prediktorvariablene ved å bruke hovedkomponentanalyse, og bruker deretter de reduserte variablene i en OLS-regresjonspasning. Selv om det ofte fungerer bra i praksis, er det ingen generell teoretisk grunn til at den mest informative lineære funksjonen til prediktorvariablene skal ligge blant de dominerende hovedkomponentene i den multivariate fordelingen av prediktorvariablene. Den delvise minste kvadraters regresjon er forlengelsen av PCR -metoden som ikke lider av den nevnte mangelen.
- Minste vinkelregresjon er en estimeringsprosedyre for lineære regresjonsmodeller som ble utviklet for å håndtere høydimensjonale kovariatvektorer, potensielt med flere kovariater enn observasjoner.
- Den Theil-Sen estimatoren er en enkel robust estimeringsteknikk som velger helningen av den tilpassede linjen for å være median av skråningene av linjer gjennom parene av samplingspunkter. Den har lignende statistiske effektivitetsegenskaper som enkel lineær regresjon, men er mye mindre følsom for ekstremer .
- Andre robuste estimeringsteknikker, inkludert α-trimmet gjennomsnittsmetode , og L-, M-, S- og R-estimatorer er introdusert.
applikasjoner
Lineær regresjon er mye brukt i biologiske, atferds- og samfunnsvitenskap for å beskrive mulige forhold mellom variabler. Det er et av de viktigste verktøyene som brukes i disse fagområdene.
Trendlinje
En trendlinje representerer en trend, den langsiktige bevegelsen i tidsseriedata etter at andre komponenter er redegjort for. Den forteller om et bestemt datasett (si BNP, oljepris eller aksjekurser) har økt eller gått ned over tid. En trendlinje kan ganske enkelt trekkes med øyet gjennom et sett med datapunkter, men mer riktig blir deres posisjon og skråning beregnet ved hjelp av statistiske teknikker som lineær regresjon. Trendlinjer er vanligvis rette linjer, selv om noen variasjoner bruker polynom av høyere grad avhengig av ønsket krumningsgrad på linjen.
Trendlinjer brukes noen ganger i forretningsanalyse for å vise endringer i data over tid. Dette har fordelen av å være enkelt. Trendlinjer brukes ofte for å argumentere for at en bestemt handling eller hendelse (for eksempel trening eller en reklamekampanje) forårsaket observerte endringer på et tidspunkt. Dette er en enkel teknikk, og krever ikke en kontrollgruppe, eksperimentell design eller en sofistikert analyseteknikk. Det lider imidlertid av mangel på vitenskapelig validitet i tilfeller der andre potensielle endringer kan påvirke dataene.
Epidemiologi
Tidlige bevis på tobakkrøyking til dødelighet og sykelighet kom fra observasjonsstudier som benyttet regresjonsanalyse. For å redusere falske korrelasjoner ved analyse av observasjonsdata, inkluderer forskere vanligvis flere variabler i sine regresjonsmodeller i tillegg til variabelen av primærinteresse. For eksempel, i en regresjonsmodell der sigarettrøyking er den uavhengige variabelen av primær interesse og den avhengige variabelen er levetid målt i år, kan forskere inkludere utdanning og inntekt som ytterligere uavhengige variabler, for å sikre at enhver observert effekt av røyking på levetiden er ikke på grunn av de andre sosioøkonomiske faktorene . Imidlertid er det aldri mulig å inkludere alle mulige forvirrende variabler i en empirisk analyse. For eksempel kan et hypotetisk gen øke dødeligheten og også føre til at folk røyker mer. Av denne grunn er randomiserte kontrollerte studier ofte i stand til å generere mer overbevisende bevis på årsakssammenhenger enn det som kan oppnås ved bruk av regresjonsanalyser av observasjonsdata. Når kontrollerte eksperimenter ikke er gjennomførbare, kan varianter av regresjonsanalyse som instrumentelle variabler regresjon brukes for å prøve å estimere årsakssammenhenger fra observasjonsdata.
Finansiere
Den kapitalverdimodellen benytter lineær regresjon samt begrepet beta for å analysere og kvantifisere systematisk risiko for en investering. Dette kommer direkte fra betakoeffisienten til den lineære regresjonsmodellen som knytter avkastningen på investeringen til avkastningen på alle risikofylte eiendeler.
Økonomi
Lineær regresjon er det dominerende empiriske verktøyet innen økonomi . For eksempel brukes det til å forutsi forbruksutgifter , faste investeringsutgifter , lagerinvestering , kjøp av et lands eksport , forbruk på import , etterspørselen etter å beholde likvide eiendeler , etterspørsel etter arbeidskraft og arbeidstilbud .
Miljøvitenskap
Lineær regresjon finner anvendelse i et bredt spekter av miljøvitenskapelige applikasjoner. I Canada bruker Environmental Effects Monitoring Program statistiske analyser på fisk og bunnundersøkelser for å måle effekten av massefabrikk eller metallgruveutløp på det akvatiske økosystemet.
Maskinlæring
Lineær regresjon spiller en viktig rolle i underfeltet til kunstig intelligens kjent som maskinlæring . Den lineære regresjonsalgoritmen er en av de grunnleggende overvåkede maskinlæringsalgoritmene på grunn av sin relative enkelhet og velkjente egenskaper.
Historie
Minste kvadrater lineær regresjon, som et middel til å finne en god grov lineær tilpasning til et sett med punkter ble utført av Legendre (1805) og Gauss (1809) for å forutsi planetarisk bevegelse. Quetelet var ansvarlig for å gjøre prosedyren kjent og for å bruke den mye i samfunnsvitenskap.
Se også
- Analyse av varianter
- Nedbrytning av blinder - Oaxaca
- Sensurert regresjonsmodell
- Tverrsnittsregresjon
- Kurvetilpasning
- Empiriske Bayes -metoder
- Feil og rester
- Summen av firkanter som er mangelfull
- Linjefitting
- Lineær klassifisering
- Lineær ligning
- Logistisk regresjon
- M-estimator
- Multivariat adaptiv regresjonsspline
- Ikke -lineær regresjon
- Ikke -parametrisk regresjon
- Normale ligninger
- Projeksjon jakt regresjon
- Responsmodelleringsmetodikk
- Segmentert lineær regresjon
- Trinnvis regresjon
- Strukturell pause
- Støtter vektormaskin
- Avkortet regresjonsmodell
- Deming regresjon
Referanser
Sitater
Kilder
- Cohen, J., Cohen P., West, SG, & Aiken, LS (2003). Anvendt multiple regresjon/korrelasjonsanalyse for atferdsvitenskapene . (2. utg.) Hillsdale, NJ: Lawrence Erlbaum Associates
- Charles Darwin . Variasjonen av dyr og planter under domesticering . (1868) (Kapittel XIII beskriver det som var kjent om reversering på Galtons tid. Darwin bruker begrepet "reversering".)
- Draper, NR; Smith, H. (1998). Anvendt regresjonsanalyse (3. utg.). John Wiley. ISBN 978-0-471-17082-2.
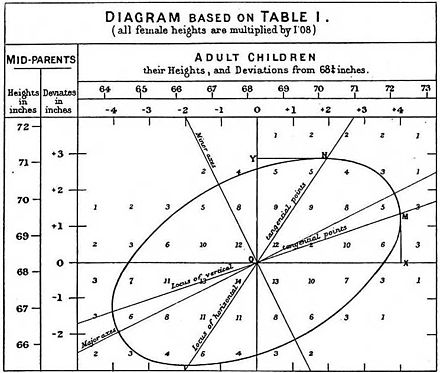
- Francis Galton. "Regresjon mot middelmådighet i arvelig statur," Journal of the Anthropological Institute , 15: 246-263 (1886). (Faks på: [1] )
- Robert S. Pindyck og Daniel L. Rubinfeld (1998, 4t red.). Econometriske modeller og økonomiske prognoser , kap. 1 (Intro, inkl. Vedlegg om Σ operatører & avledning av parameterest.) & Vedlegg 4.3 (multiregresjon i matriseform).
Videre lesning
- Pedhazur, Elazar J (1982). Multipel regresjon i atferdsforskning: Forklaring og prediksjon (2. utg.). New York: Holt, Rinehart og Winston. ISBN 978-0-03-041760-3.
- Mathieu Rouaud, 2013: Sannsynlighet, statistikk og estimering Kapittel 2: Lineær regresjon, lineær regresjon med feillinjer og ikke -lineær regresjon.
- National Physical Laboratory (1961). "Kapittel 1: Lineære ligninger og matriser: Direkte metoder". Moderne databehandlingsmetoder . Notater om anvendt vitenskap. 16 (2. utg.). Hennes majestets skrivesaker .
Eksterne linker
- Minste kvadraters regresjon , PhET interaktive simuleringer, University of Colorado at Boulder
- DIY lineær passform






























![{\ displaystyle {\ vec {x_ {i}}} = \ venstre [x_ {1}^{i}, x_ {2}^{i}, \ ldots, x_ {m}^{i} \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/156ecace8a311d501c63ca49c73bba6efc915283)
![{\ displaystyle {\ vec {\ beta}} = \ venstre [\ beta _ {0}, \ beta _ {1}, \ ldots, \ beta _ {m} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32434f0942d63c868f23d5af39442bb90783633b)


![{\ displaystyle {\ vec {x_ {i}}} = \ venstre [1, x_ {1}^{i}, x_ {2}^{i}, \ ldots, x_ {m}^{i} \ høyre ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72fa7acd1682497c285884b0686d784d8b0eb15)








