Maksimal kraftoverføringsteorem - Maximum power transfer theorem

I elektroteknikk sier teoremet om maksimal kraftoverføring at for å få maksimal ekstern effekt fra en kilde med en endelig indre motstand , må belastningenes motstand være lik motstanden til kilden sett fra dens utgangsterminaler. Moritz von Jacobi publiserte maksimal effekt (overføring) teoremet rundt 1840; den blir også referert til som " Jacobis lov ".

Den teorem gir maksimal effektoverføring over kretsen, og ikke maksimal effektivitet . Hvis motstanden til lasten blir større enn motstanden til kilden, er effektiviteten høyere, siden en høyere prosentandel av kildeeffekten overføres til lasten, men størrelsen på lasteffekten er lavere siden den totale kretsmotstanden øker.

Hvis belastningsmotstanden er mindre enn kildemotstanden, ender det med at mesteparten av kraften forsvinner i kilden, og selv om den totale effekten som er spredt er høyere, på grunn av en lavere total motstand, viser det seg at mengden som forsvinner i lasten er redusert.

Teoremet sier hvordan du skal velge (for å maksimere kraftoverføringen) lastmotstanden når kildemotstanden er gitt. Det er en vanlig misforståelse å bruke teoremet i motsatt scenario. Det står ikke hvordan du skal velge kildemotstand for en gitt lastmotstand. Faktisk er kildemotstanden som maksimerer kraftoverføring fra en spenningskilde alltid null, uavhengig av verdien av belastningsmotstanden.

Teoremet kan utvides til vekselstrømskretser som inkluderer reaktans , og sier at maksimal kraftoverføring oppstår når lastimpedansen er lik det komplekse konjugatet til kildeimpedansen.

Nylige eksponeringsartikler illustrerer hvordan den grunnleggende matematikken til maksimal effektteorem også gjelder andre fysiske situasjoner, for eksempel:

mekaniske kollisjoner mellom to gjenstander,
deling av ladning mellom to kondensatorer,
væskestrøm mellom to sylindere
overføring og refleksjon av lys ved grensen mellom to medier

Maksimering av kraftoverføring kontra strømeffektivitet

Teoremet ble opprinnelig misforstått (spesielt av Joule ) for å antyde at et system bestående av en elektrisk motor drevet av et batteri ikke kunne være mer enn 50% effektivt siden, når impedansene ble matchet, tapte effekten som varme i batteriet alltid være lik kraften som leveres til motoren.

I 1880 ble denne antagelsen vist å være falsk av enten Edison eller hans kollega Francis Robbins Upton , som innså at maksimal effektivitet ikke var det samme som maksimal kraftoverføring.

For å oppnå maksimal effektivitet kan motstanden til kilden (enten et batteri eller en dynamo ) gjøres (eller burde være) så nær null som mulig. Ved å bruke denne nye forståelsen oppnådde de en effektivitet på omtrent 90%, og beviste at elmotoren var et praktisk alternativ til varmemotoren .

Betingelsen for maksimal kraftoverføring resulterer ikke i maksimal effektivitet .

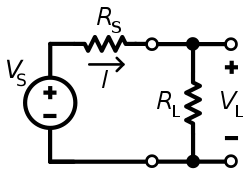
Hvis vi definerer virkningsgraden $η$ som forholdet mellom kraften som spres av lasten, R _L , til effekten utviklet av kilden, V _S , er det enkelt å beregne ut fra kretsdiagrammet ovenfor at

{\ displaystyle \ eta = {\ frac {R _ {\ mathrm {L}}} {R _ {\ mathrm {L}}+R _ {\ mathrm {S}}}} = {\ frac {1} {1+R_ {\ mathrm {S}}/R _ {\ mathrm {L}}}}.}

Vurder tre spesielle tilfeller:

Hvis , da ${\ displaystyle R _ {\ mathrm {L}} = R _ {\ mathrm {S}}}$ ${\ displaystyle \ eta = 0,5,}$
Hvis eller da ${\ displaystyle R _ {\ mathrm {L}} \ to \ infty}$ ${\ displaystyle R _ {\ mathrm {S}} = 0,}$ ${\ displaystyle \ eta = 1,}$
Hvis , da ${\ displaystyle R _ {\ mathrm {L}} = 0}$ ${\ displaystyle \ eta = 0.}$

Effektiviteten er bare 50% når maksimal kraftoverføring oppnås, men nærmer seg 100% når belastningsmotstanden nærmer seg uendelig, selv om det totale effektnivået har en tendens til null.

Effektivitet nærmer seg også 100% hvis kildemotstanden nærmer seg null, og 0% hvis lastmotstanden nærmer seg null. I sistnevnte tilfelle forbrukes all strøm inne i kilden (med mindre kilden heller ikke har motstand), så strømmen som forsvinner i en kortslutning er null.

Impedansmatching

Et beslektet konsept er refleksløs impedansmatching .

I radiofrekvenstransmisjonslinjer , og andre elektronikk , er det ofte et behov for å samsvare med kildeimpedansen (i senderen) til lastimpedansen (slik som en antenne ) for å unngå refleksjoner i overføringslinjen som kan overbelaste eller skade transmitteren.

Beregningsbasert bevis for rent resistive kretser

I diagrammet på motsatt side, blir kraften som overføres fra kilden, med spenning $V$ og fast kildemotstand $R S$ , til en belastning med motstand $R L$ , noe som resulterer i en strøm $I$ . Etter Ohms lov er $jeg$ ganske enkelt kildespenningen delt på den totale kretsmotstanden:

{\ displaystyle I = {\ frac {V} {R _ {\ mathrm {S}}+R _ {\ mathrm {L}}}}.}

Effekten $P L$ spredt i lasten er kvadratet av strømmen multiplisert med motstanden:

{\ displaystyle P _ {\ mathrm {L}} = I^{2} R _ {\ mathrm {L}} = \ left ({\ frac {V} {R _ {\ mathrm {S}}+R _ {\ mathrm { L}}}} \ høyre)^{2} R _ {\ mathrm {L}} = {\ frac {V^{2}} {R _ {\ mathrm {S}}^{2}/R _ {\ mathrm { L}}+2R _ {\ mathrm {S}}+R _ {\ mathrm {L}}}}.}

Verdien av $R L$ som dette uttrykket er et maksimum for kan beregnes ved å differensiere det, men det er lettere å beregne verdien av $R L$ som nevneren er for

{\ displaystyle R _ {\ mathrm {S}}^{2}/R _ {\ mathrm {L}}+2R _ {\ mathrm {S}}+R _ {\ mathrm {L}}}

er et minimum. Resultatet blir det samme i begge tilfeller. Å skille nevneren med hensyn til $R L$ :

{\ displaystyle {\ frac {d} {dR _ {\ mathrm {L}}}} \ venstre (R _ {\ mathrm {S}}^{2}/R _ {\ mathrm {L}}+2R _ {\ mathrm { S}}+R _ {\ mathrm {L}} \ right) =-R _ {\ mathrm {S}}^{2}/R _ {\ mathrm {L}}^{2} +1.}

For et maksimum eller minimum er det første derivatet null, så

{\ displaystyle R _ {\ mathrm {S}}^{2}/R _ {\ mathrm {L}}^{2} = 1}

eller

{\ displaystyle R _ {\ mathrm {L}} = \ pm R _ {\ mathrm {S}}.}

I praktiske resistive kretser, $R S$ og $R L$ begge er positive, slik at det positive tegn i det ovenstående er den riktige løsning.

For å finne ut om denne løsningen er et minimum eller et maksimum, differensieres nevneren uttrykket igjen:

{\ displaystyle {{d^{2}} \ over {dR _ {\ mathrm {L}}^{2}}} \ venstre ({R _ {\ mathrm {S}}^{2}/R _ {\ mathrm { L}}+2R _ {\ mathrm {S}}+R _ {\ mathrm {L}}} \ right) = {2R _ {\ mathrm {S}}^{2}}/{R _ {\ mathrm {L}} ^{3}}. \, \!}

Dette er alltid positivt for positive verdier av og , som viser at nevneren er et minimum, og effekten er derfor et maksimum, når ${\ displaystyle R _ {\ mathrm {S}} \, \!}$ ${\ displaystyle R _ {\ mathrm {L}} \, \!}$

{\ displaystyle R _ {\ mathrm {S}} = R _ {\ mathrm {L}}. \, \!}

Ovennevnte bevis forutsetter fast kildebestandighet . Når kildemotstanden kan varieres, kan effekten som overføres til lasten økes ved å redusere . For eksempel vil en 100 Volt -kilde med en av levere 250 watt strøm til en last; reduserer til øker effekten levert til 1000 watt. ${\ displaystyle R _ {\ mathrm {S}} \, \!}$ ${\ displaystyle R _ {\ textrm {S}} \, \!}$ ${\ displaystyle R _ {\ textrm {S}} \, \!}$ ${\ displaystyle 10 ~ \ Omega}$ ${\ displaystyle 10 ~ \ Omega}$ ${\ displaystyle R _ {\ textrm {S}} \, \!}$ ${\ displaystyle 0 ~ \ Omega}$

Vær oppmerksom på at dette viser at maksimal kraftoverføring også kan tolkes som at belastningsspenningen er lik halvparten av Thevenin-spenningsekvivalenten til kilden.

I reaktive kretser

Kraftoverføringssetningen gjelder også når kilden og/eller belastningen ikke er rent motstandsdyktig.

En foredling av maksimal effektteorem sier at alle reaktive komponenter i kilde og belastning bør være av samme størrelse, men motsatt tegn. ( Se nedenfor for en avledning. )

Dette betyr at kilde- og lastimpedansene skal være komplekse konjugater av hverandre.
Når det gjelder rent resistive kretser, er de to konseptene identiske.

Fysisk realiserbare kilder og belastninger er vanligvis ikke rent resistive, og har noen induktive eller kapasitive komponenter, og det finnes derfor praktiske anvendelser av denne setningen, under navnet komplekst konjugatimpedansmatching.

Hvis kilden er totalt induktiv (kapasitiv), vil en helt kapasitiv (induktiv) belastning, uten fragivende resistive tap, motta 100% av energien fra kilden, men sende den tilbake etter en kvart syklus.

Den resulterende kretsen er ingenting annet enn en resonant LC -krets der energien fortsetter å svinge frem og tilbake. Denne svingningen kalles reaktiv effekt .

Effektfaktorkorreksjon (der en induktiv reaktans brukes for å "balansere ut" en kapasitiv), er i hovedsak den samme ideen som kompleks konjugert impedansmatching, selv om det gjøres av helt andre grunner.

For en fast reaktiv kilde maksimerer maksimal effektteorem den virkelige effekten (P) som leveres til lasten ved komplekst konjugat som matcher lasten til kilden.

For en fast reaktiv belastning minimerer effektfaktorkorreksjon den tilsynelatende effekten (S) (og unødvendig strøm) utført av overføringslinjene, samtidig som den opprettholder samme mengde ekte kraftoverføring.

Dette gjøres ved å legge en reaktans til lasten for å balansere lastens egen reaktans, endre den reaktive lastimpedansen til en resistiv lastimpedans.

Bevis

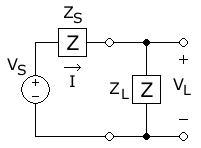
I dette diagrammet overføres vekselstrøm fra kilden, med fasestørrelse av spenning (positiv toppspenning) og fast kildeimpedans (S for kilde), til en belastning med impedans (L for belastning), noe som resulterer i en (positiv) størrelsen på den nåværende fasoren . Denne størrelsen kommer fra å dele størrelsen på kildespenningen med størrelsen på den totale kretsimpedansen: ${\ displaystyle | V _ {\ text {S}} |}$ ${\ displaystyle Z _ {\ text {S}}}$ ${\ displaystyle Z _ {\ text {L}}}$ ${\ displaystyle | I |}$ ${\ displaystyle I}$ ${\ displaystyle | I |}$

{\ displaystyle | I | = {| V _ {\ text {S}} | \ over | Z _ {\ text {S}}+Z _ {\ text {L}} |}.}

Gjennomsnittlig effekt spredt i lasten er kvadratet av strømmen multiplisert med den resistive delen (den virkelige delen) av lastimpedansen : ${\ displaystyle P _ {\ text {L}}}$ ${\ displaystyle R _ {\ text {L}}}$ ${\ displaystyle Z _ {\ text {L}}}$

{\ displaystyle {\ begin {align} P _ {\ text {L}} & = I _ {\ text {rms}}^{2} R _ {\ text {L}} = {1 \ over 2} | I |^ {2} R _ {\ text {L}} \\ & = {1 \ over 2} \ left ({| V _ {\ text {S}} | \ over | Z _ {\ text {S}}+Z _ {\ tekst {L}} |} \ høyre)^{2} R _ {\ tekst {L}} = {1 \ over 2} {| V _ {\ tekst {S}} |^{2} R _ {\ tekst {L }} \ over (R _ {\ tekst {S}}+R _ {\ tekst {L}})^{2}+(X _ {\ tekst {S}}+X _ {\ tekst {L}})^{2 }}, \ end {align}}}

hvor og angir motstandene, det vil si de virkelige delene, og og betegner reaktansene, det vil si de imaginære delene, av henholdsvis kilde- og lastimpedansene og . ${\ displaystyle R _ {\ text {S}}}$ ${\ displaystyle R _ {\ text {L}}}$ ${\ displaystyle X _ {\ text {S}}}$ ${\ displaystyle X _ {\ text {L}}}$ ${\ displaystyle Z _ {\ text {S}}}$ ${\ displaystyle Z _ {\ text {L}}}$

For å bestemme, for en gitt kildespenning og impedans verdien av lastimpedansen som dette uttrykket for effekten gir maksimum for, finner man først, for hver fast positiv verdi , verdien av det reaktive uttrykket som nevneren for ${\ displaystyle V _ {\ text {S}}}$ ${\ displaystyle Z _ {\ text {S}},}$ ${\ displaystyle Z _ {\ text {L}},}$ ${\ displaystyle R _ {\ text {L}}}$ ${\ displaystyle X _ {\ text {L}}}$

{\ displaystyle (R _ {\ tekst {S}}+R _ {\ tekst {L}})^{2}+(X _ {\ tekst {S}}+X _ {\ tekst {L}})^{2} \,}

er et minimum. Siden reaktanser kan være negative, oppnås dette ved å tilpasse lastreaktansen til

{\ displaystyle X _ {\ text {L}} =-X _ {\ text {S}}.}

Dette reduserer ligningen ovenfor til:

{\ displaystyle P _ {\ text {L}} = {\ frac {1} {2}} {\ frac {| V _ {\ text {S}} |^{2} R _ {\ text {L}}} { (R _ {\ tekst {S}}+R _ {\ tekst {L}})^{2}}}}

og det gjenstår å finne verdien som maksimerer dette uttrykket. Dette problemet har samme form som i det rent resistive tilfellet, og maksimaliseringsbetingelsen er derfor ${\ displaystyle R _ {\ text {L}}}$ ${\ displaystyle R _ {\ text {L}} = R _ {\ text {S}}.}$

De to maksimeringsforholdene

${\ displaystyle R _ {\ text {L}} = R _ {\ text {S}}}$
${\ displaystyle X _ {\ text {L}} =-X _ {\ text {S}}}$

beskrive det komplekse konjugatet til kildeimpedansen, betegnet med og dermed kan kortfattet kombineres til: ${\ displaystyle ^{*},}$

{\ displaystyle Z _ {\ text {L}} = Z _ {\ text {S}}^{*}.}

Merknader

^ Thompson Phillips (2009-05-30), Dynamo-Electric Machinery; En håndbok for studenter ved elektroteknikk , BiblioBazaar, LLC, ISBN 978-1-110-35104-6
^ ^a ^b Harrison, Mark (2013-02-22). "Fysiske kollisjoner og maksimal effektteorem: en analogi mellom mekaniske og elektriske situasjoner". Fysikkopplæring . 48 (2): 207–211. doi : 10.1088/0031-9120/48/2/207 . ISSN 0031-9120 .
^ Atkin, Keith (2013-08-22). "Energioverføring og en tilbakevendende matematisk funksjon". Fysikkopplæring . 48 (5): 616–620. doi : 10.1088/0031-9120/48/5/616 . ISSN 0031-9120 .
^ "Grunnleggende elektronikkopplæringer og revisjon for nybegynnere til videregående elever" .

Referanser

HW Jackson (1959) Introduction to Electronic Circuits, Prentice-Hall.

Eksterne linker

[1] Thompson Phillips (2009-05-30), Dynamo-Electric Machinery; En håndbok for studenter ved elektroteknikk , BiblioBazaar, LLC, ISBN 978-1-110-35104-6

[harrison2013-2] Harrison, Mark (2013-02-22). "Fysiske kollisjoner og maksimal effektteorem: en analogi mellom mekaniske og elektriske situasjoner". Fysikkopplæring . 48 (2): 207–211. doi : 10.1088/0031-9120/48/2/207 . ISSN 0031-9120 .

[3] Atkin, Keith (2013-08-22). "Energioverføring og en tilbakevendende matematisk funksjon". Fysikkopplæring . 48 (5): 616–620. doi : 10.1088/0031-9120/48/5/616 . ISSN 0031-9120 .

[4] "Grunnleggende elektronikkopplæringer og revisjon for nybegynnere til videregående elever" .

Languages

In other projects