Stående bølge - Standing wave

Animasjon av en stående bølge ( rød ) skapt av superposisjonen til en venstre reiser ( blå ) og høyre reiser ( grønn ) bølge

I fysikken er en stående bølge , også kjent som en stasjonær bølge , en bølge som svinger i tid, men hvis toppamplitudeprofil ikke beveger seg i rommet. Toppen amplitude av bølge svingninger ved et hvilket som helst punkt i rommet er konstant med hensyn til tid, og de svingninger på forskjellige steder i hele bølge er i fase . Stedene hvor den absolutte verdien av amplituden er minimum kalles noder , og stedene der den absolutte verdien av amplituden er maksimal kalles antinoder .

Stående bølger ble først lagt merke til av Michael Faraday i 1831. Faraday observerte stående bølger på overflaten av en væske i en vibrerende beholder. Franz Melde skapte begrepet "stående bølge" (tysk: stehende Welle eller Stehwelle ) rundt 1860 og demonstrerte fenomenet i sitt klassiske eksperiment med vibrerende strenger.

Dette fenomenet kan oppstå fordi mediet beveger seg i motsatt retning av bølgen, eller det kan oppstå i et stasjonært medium som et resultat av interferens mellom to bølger som beveger seg i motsatte retninger. Den vanligste årsaken til stående bølger er fenomenet resonans , der stående bølger oppstår inne i en resonator på grunn av interferens mellom bølger som reflekteres frem og tilbake ved resonatorens resonansfrekvens .

For bølger med samme amplitude som beveger seg i motsatte retninger, er det i gjennomsnitt ingen nettoverbredelse av energi .

Flyttende medium

Spill media

Kajakkpadlere surfer på en stående bølge i Great Falls National Park .

Som et eksempel på den første typen, under visse meteorologiske forhold stående bølger dannes i atmosfæren i le av fjellkjeder. Slike bølger utnyttes ofte av seilflypiloter .

Stående bølger og hydrauliske hopp dannes også på hurtigflytende elvstryk og tidevannsstrømmer som Saltstraumen malstrøm . Mange stående elvebølger er populære elvesurfer .

Motstridende bølger

Som et eksempel på den andre typen er en stående bølge i en overføringslinje en bølge der fordelingen av strøm , spenning eller feltstyrke dannes ved overlagring av to bølger med samme frekvens som forplanter seg i motsatte retninger. Effekten er en serie noder (null forskyvning ) og antinoder (maksimal forskyvning ) på faste punkter langs overføringslinjen. En slik stående bølge kan dannes når en bølge sendes inn i den ene enden av en overføringslinje og reflekteres fra den andre enden av en impedans -mismatch , dvs. diskontinuitet, for eksempel en åpen krets eller en kortslutning . Linjens svikt i å overføre kraft ved stående bølgefrekvens vil vanligvis resultere i dempningsforvrengning .

I praksis betyr tap i overføringslinjen og andre komponenter at en perfekt refleksjon og en ren stående bølge aldri oppnås. Resultatet er en delvis stående bølge , som er en superposisjon av en stående bølge og en bevegelige bølge. I hvilken grad bølgen ligner enten en ren stående bølge eller en ren bevegelige bølge måles ved stående bølgeforhold (SWR).

Et annet eksempel er stående bølger i det åpne havet dannet av bølger med samme bølgetid som beveger seg i motsatte retninger. Disse kan danne nær stormsentre, eller fra refleksjon av en svelning ved kysten, og er kilden til mikrobarmer og mikroseismer .

Matematisk beskrivelse

Denne delen tar for seg representative en- og todimensjonale tilfeller av stående bølger. For det første viser et eksempel på en uendelig lengde streng hvordan identiske bølger som beveger seg i motsatte retninger forstyrrer å produsere stående bølger. Deretter viser to begrensede lengdeeksempler med forskjellige grensebetingelser hvordan grensebetingelsene begrenser frekvensene som kan danne stående bølger. Deretter demonstrerer eksemplet på lydbølger i et rør hvordan de samme prinsippene kan brukes på langsgående bølger med analoge grensebetingelser.

Stående bølger kan også forekomme i to- eller tredimensjonale resonatorer . Med stående bølger på todimensjonale membraner som trommehoder , illustrert i animasjonene ovenfor, blir nodene knutelinjer, linjer på overflaten der det ikke er bevegelse, som skiller områder som vibrerer med motsatt fase. Disse nodal linjemønstrene kalles Chladni -figurer . I tredimensjonale resonatorer, for eksempel lydboks for musikkinstrumenter og resonatorer i mikrobølgeovn , er det nodale overflater. Denne seksjonen inkluderer et todimensjonalt stående bølgeeksempel med en rektangulær grense for å illustrere hvordan konseptet kan utvides til høyere dimensjoner.

Stående bølge på en uendelig lengde

For å begynne, bør du vurdere en streng med uendelig lengde langs x -aksen som er fri til å bli strukket på tvers i y -retningen.

For en harmonisk bølge som reiser til høyre langs strengen, strengens forskyvning i y- retningen som en funksjon av posisjon x , og tiden t er

${\ displaystyle y _ {\ text {R}} (x, t) = y _ {\ text {max}} \ sin \ left ({2 \ pi x \ over \ lambda}-\ omega t \ right).}$

Forskyvningen i y -retningen for en identisk harmonisk bølge som beveger seg til venstre er

${\ displaystyle y _ {\ text {L}} (x, t) = y _ {\ text {max}} \ sin \ left ({2 \ pi x \ over \ lambda}+\ omega t \ right),}$

hvor

• y _max er amplituden til forskyvningen av strengen for hver bølge,
• ω er vinkelfrekvensen eller tilsvarende 2π ganger frekvensen f ,
• λ er bølgelengden til bølgen.

For identiske høyre- og venstrebølgende bølger på samme streng, er den totale forskyvningen av strengen summen av y _R og y _L ,

${\ displaystyle y (x, t) = y _ {\ text {R}}+y _ {\ text {L}} = y _ {\ text {max}} \ sin \ left ({2 \ pi x \ over \ lambda }-\ omega t \ right)+y _ {\ text {max}} \ sin \ left ({2 \ pi x \ over \ lambda}+\ omega t \ right).}$

Ved å bruke den trigonometriske summen til produktidentiteten , ${\ displaystyle \ sin a+\ sin b = 2 \ sin \ left ({a+b \ over 2} \ right) \ cos \ left ({ab \ over 2} \ right)}$

${\ displaystyle y (x, t) = 2y _ {\ text {max}} \ sin \ left ({2 \ pi x \ over \ lambda} \ right) \ cos (\ omega t).}$

( 1 )

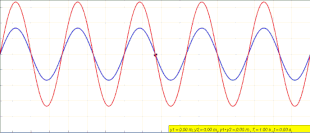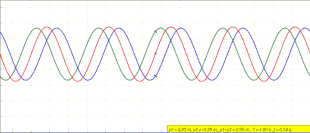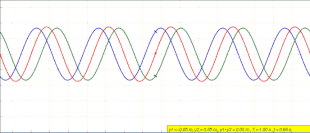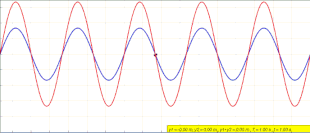
Vær oppmerksom på at ligning ( 1 ) ikke beskriver en bevegelige bølge. I hvilken som helst posisjon x , svinger y ( x , t ) rett og slett i tid med en amplitude som varierer i x -retningen som . Animasjonen i begynnelsen av denne artikkelen skildrer hva som skjer. Etter hvert som den venstrebårende blå bølgen og den høyre-grønnbølgen forstyrrer, danner de den stående røde bølgen som ikke beveger seg og i stedet svinger på plass. ${\ displaystyle 2y _ {\ text {max}} \ sin \ left ({2 \ pi x \ over \ lambda} \ right)}$

Fordi strengen er av uendelig lengde, har den ingen grensebetingelser for forskyvning på noe tidspunkt langs x -aksen. Som et resultat kan en stående bølge dannes med hvilken som helst frekvens.

På steder på x -aksen som er til og med multipler av en kvart bølgelengde,

${\ displaystyle x = \ ldots,-{3 \ lambda \ over 2}, \;-\ lambda, \;-{\ lambda \ over 2}, \; 0, \; {\ lambda \ over 2}, \ ; \ lambda, \; {3 \ lambda \ over 2}, \ ldots}$

amplituden er alltid null. Disse stedene kalles noder . På steder på x -aksen som er oddetall av en kvart bølgelengde

${\ displaystyle x = \ ldots,-{5 \ lambda \ over 4}, \;-{3 \ lambda \ over 4}, \;-{\ lambda \ over 4}, \; {\ lambda \ over 4} , \; {3 \ lambda \ over 4}, \; {5 \ lambda \ over 4}, \ ldots}$

amplituden er maksimal, med en verdi på det dobbelte av amplituden til de høyre og venstre bevegelige bølgene som forstyrrer for å produsere dette stående bølgemønsteret. Disse stedene kalles antinoder . Avstanden mellom to påfølgende noder eller antinoder er halv bølgelengde, λ /2.

Stående bølge på en streng med to faste ender

Neste vurdere en streng med faste ender ved x = 0 og x = L . Strengen vil ha en viss demping da den strekkes av bevegelige bølger, men antar at dempningen er veldig liten. Anta at den x = 0 faste enden påføres en sinusformet kraft som driver strengen opp og ned i y-retningen med en liten amplitude ved en eller annen frekvens f . I denne situasjonen produserer drivkraften en høyresvingende bølge. Den bølgen reflekterer fra den høyre faste enden og beveger seg tilbake til venstre, reflekterer igjen fra den venstre faste enden og beveger seg tilbake til høyre, og så videre. Til slutt oppnås en jevn tilstand der strengen har identiske høyre- og venstrebølgende bølger som i tilfellet med uendelig lengde, og kraften som forsvinner ved demping i strengen er lik kraften som tilføres av drivkraften, slik at bølgene har konstant amplitude.

Ligning ( 1 ) beskriver fremdeles det stående bølgemønsteret som kan dannes på denne strengen, men nå er ligning ( 1 ) underlagt grensebetingelser der y = 0 ved x = 0 og x = L fordi strengen er fikset til x = L og fordi vi antar at drivkraften i den faste x = 0 enden har liten amplitude. Kontrollere verdiene til y i de to endene,

${\ displaystyle y (0, t) = 0,}$

${\ displaystyle y (L, t) = 2y _ {\ text {max}} \ sin \ left ({2 \ pi L \ over \ lambda} \ right) \ cos (\ omega t) = 0.}$

Stående bølger i en streng - den grunnleggende modusen og de fem første harmoniske .

Sistnevnte grensebetingelse er oppfylt når . L er gitt, så grensetilstanden begrenser bølgelengden til de stående bølgene til ${\ displaystyle \ sin \ left ({2 \ pi L \ over \ lambda} \ right) = 0}$

${\ displaystyle \ lambda = {\ frac {2L} {n}},}$

( 2 )

${\ displaystyle n = 1,2,3, \ ldots}$

Bølgene kan bare danne stående bølger på denne strengen om de har en bølgelengde som tilfredsstiller dette forhold med L . Hvis bølger beveger seg med hastigheten v langs strengen, er frekvensen til de stående bølgene ekvivalent begrenset til

${\ displaystyle f = {\ frac {v} {\ lambda}} = {\ frac {nv} {2L}}.}$

Den stående bølgen med n = 1 svinger ved grunnfrekvensen og har en bølgelengde som er dobbelt så lang som strengen. Høyere heltallverdier av n tilsvarer svingningsmåter som kalles harmoniske eller overtoner . Enhver stående bølge på strengen vil ha n + 1 noder inkludert de faste endene og n antinoder.

For å sammenligne dette eksemplets noder med beskrivelsen av noder for stående bølger i strengen med uendelig lengde, merk at ligning ( 2 ) kan skrives om som

${\ displaystyle \ lambda = {\ frac {4L} {n}},}$

${\ displaystyle n = 2,4,6, \ ldots}$

I denne variasjonen av uttrykket for bølgelengden må n være jevn. Kryssmultiplikasjon ser vi at fordi L er en node, er det et jevnt multiplum av en kvart bølgelengde,

${\ displaystyle L = {\ frac {n \ lambda} {4}},}$

${\ displaystyle n = 2,4,6, \ ldots}$

Dette eksemplet demonstrerer en type resonans og frekvensene som produserer stående bølger kan refereres til som resonansfrekvenser .

Stående bølge på en streng med en fast ende

Forbigående analyse av en dempet vandrende bølge som reflekterer ved en grense.

Vurder deretter den samme strengen med lengde L , men denne gangen er den bare fikset til x = 0 . Ved x = L er strengen fri til å bevege seg i y -retningen. For eksempel kan strengen være bundet x = L til en ring som kan gli fritt opp og ned en stang. Strengen har igjen liten demping og drives av en liten drivkraft på x = 0 .

I dette tilfellet beskriver ligning ( 1 ) fremdeles det stående bølgemønsteret som kan dannes på strengen, og strengen har samme grensetilstand y = 0 ved x = 0 . Imidlertid, ved x = L hvor strengen kan bevege seg fritt, bør det være en antinode med maksimal amplitude på y . Gjennomgang av ligning ( 1 ), for x = L oppstår den største amplituden til y når

${\ displaystyle \ sin \ left ({2 \ pi L \ over \ lambda} \ right) = 1.}$

Dette fører til et annet sett med bølgelengder enn i eksemplet med to faste ender. Her er bølgelengden til de stående bølgene begrenset til

${\ displaystyle \ lambda = {\ frac {4L} {n}},}$

${\ displaystyle n = 1,3,5, \ ldots}$

Tilsvarende er frekvensen begrenset til

${\ displaystyle f = {\ frac {nv} {4L}}.}$

Vær oppmerksom på at i dette eksemplet tar n bare merkelige verdier. Fordi L er en antinode, er det et oddetall på en kvart bølgelengde. Dermed har den grunnleggende modusen i dette eksemplet bare en fjerdedel av en komplett sinussyklus - null ved x = 0 og den første toppen ved x = L - den første harmonikken har tre fjerdedeler av en komplett sinussyklus, og så videre.

Dette eksemplet demonstrerer også en type resonans og frekvensene som produserer stående bølger kalles resonansfrekvenser .

Stående bølge i et rør

Betrakt en stående bølge i et rør av lengde L . Luften inne i røret fungerer som medium for langsgående lydbølger som beveger seg til høyre eller venstre gjennom røret. Mens de tverrgående bølgene på strengen fra de tidligere eksemplene varierer i forskyvningen deres vinkelrett på bølgebevegelsesretningen, varierer bølgene som beveger seg gjennom luften i røret når det gjelder trykk og lengdeforskyvning langs bølgebevegelsesretningen. Bølgen forplanter seg ved vekselvis å komprimere og ekspandere luft i segmenter av røret, som forskyver luften litt fra hvileposisjonen og overfører energi til nabosegmenter gjennom kreftene som utøves av det vekslende høye og lave lufttrykket. Likninger som ligner de for bølgen på en streng kan skrives for endringen i trykket Δ p på grunn av en høyre eller venstre bevegelse i røret.

${\ displaystyle \ Delta p _ {\ text {R}} (x, t) = p _ {\ text {max}} \ sin \ venstre ({2 \ pi x \ over \ lambda}-\ omega t \ right), }$

${\ displaystyle \ Delta p _ {\ text {L}} (x, t) = p _ {\ text {max}} \ sin \ venstre ({2 \ pi x \ over \ lambda}+\ omega t \ right), }$

hvor

• p _max er trykkamplituden eller maksimal økning eller reduksjon i lufttrykket på grunn av hver bølge,
• ω er vinkelfrekvensen eller tilsvarende 2π ganger frekvensen f ,
• λ er bølgelengden til bølgen.

Hvis identiske høyre- og venstrebølgende bølger beveger seg gjennom røret, blir den resulterende superposisjonen beskrevet av summen

${\ displaystyle \ Delta p (x, t) = \ Delta p _ {\ text {R}} (x, t)+\ Delta p _ {\ text {L}} (x, t) = 2p _ {\ text {max }} \ sin \ venstre ({2 \ pi x \ over \ lambda} \ høyre) \ cos (\ omega t).}$

Vær oppmerksom på at denne formelen for trykket er av samme form som ligning ( 1 ), så det dannes en stasjonær trykkbølge som er fikset i rommet og svinger i tid.

Hvis enden av et rør er lukket, er trykket maksimalt siden den lukkede enden av røret utøver en kraft som begrenser luftens bevegelse. Dette tilsvarer en trykkantennode. Hvis enden av røret er åpen, er trykkvariasjonene svært små, tilsvarende en trykknode. Den nøyaktige plasseringen av trykknoden ved en åpen ende er faktisk litt utenfor rørets åpne ende, så rørets effektive lengde for å bestemme resonansfrekvenser er litt lengre enn dens fysiske lengde. Denne forskjellen i lengde blir ignorert i dette eksemplet. Når det gjelder refleksjoner, reflekterer åpne ender delvis bølger tilbake i røret, slik at noe energi kan slippes ut i luften utenfor. Ideelt sett reflekterer lukkede ender hele bølgen tilbake i den andre retningen.

Vurder først et rør som er åpent i begge ender, for eksempel et åpent orgelrør eller en opptaker . Gitt at trykket må være null i begge åpne ender, er grensebetingelsene analoge med strengen med to faste ender,

${\ displaystyle \ Delta p (0, t) = 0,}$

${\ displaystyle \ Delta p (L, t) = 2p _ {\ text {max}} \ sin \ venstre ({2 \ pi L \ over \ lambda} \ høyre) \ cos (\ omega t) = 0,}$

som bare oppstår når bølgelengden til stående bølger er

${\ displaystyle \ lambda = {\ frac {2L} {n}},}$

${\ displaystyle n = 1,2,3, \ ldots,}$

eller tilsvarende når frekvensen er

${\ displaystyle f = {\ frac {nv} {2L}},}$

hvor v er lydens hastighet .

Neste vurdere et rør som er åpent og har derfor et trykk node ved x = 0 og lukket, og derfor har et trykk som anti-noden ved x = L . Eksempler inkluderer en flaske og en klarinett . Dette røret har grensebetingelser som er analoge med strengen med bare en fast ende. Dens stående bølger har bølgelengder begrenset til

${\ displaystyle \ lambda = {\ frac {4L} {n}},}$

${\ displaystyle n = 1,3,5, \ ldots,}$

eller tilsvarende er frekvensen av stående bølger begrenset til

${\ displaystyle f = {\ frac {nv} {4L}}.}$

Vær oppmerksom på at i tilfellet der den ene enden er lukket, tar n bare oddetall verdier akkurat som for strengen som er festet til bare den ene enden.

Molekylær representasjon av en stående bølge med n = 2 for et rør som er lukket i begge ender. Vurderer langsgående forskyvning, merk at molekylene i endene og molekylene i midten ikke forskyves av bølgen, som representerer noder for langsgående forskyvning. Halvveis mellom nodene er det antennoder i lengderetningen som forskyver seg maksimalt. Med tanke på trykk, vær oppmerksom på at molekylene er maksimalt komprimert og utvidet i endene og i midten, som representerer trykkantinoder. Halvveis mellom antinodene er trykknoder der molekylene verken komprimeres eller utvides når de beveger seg.

Så langt har bølgen blitt skrevet når det gjelder trykket som en funksjon av posisjon x og tid. Alternativt kan bølgen skrives i form av dens langsgående forskyvning av luft, der luft i et segment av røret beveger seg litt frem og tilbake i x -retningen ettersom trykket varierer og bølger beveger seg i en eller begge retninger. Endringen i trykk Δ p og langsgående forskyvning s er relatert så

${\ displaystyle \ Delta p =-\ rho v^{2} {\ frac {\ delvis s} {\ delvis x}},}$

hvor ρ er luftens tetthet . Når det gjelder lengdeforskyvning, svarer lukkede ender av rør til noder siden luftbevegelse er begrenset og åpne ender tilsvarer antinoder siden luften er fri til å bevege seg. Et lignende, lettere å visualisere fenomen forekommer i langsgående bølger som forplanter seg langs en fjær.

Vi kan også vurdere et rør som er lukket i begge ender. I dette tilfellet vil begge ender være trykkantennoder eller tilsvarende vil begge ender være forskyvningsnoder. Dette eksemplet er analogt med tilfellet der begge ender er åpne, bortsett fra at det stående bølgemønsteret har et π ⁄ 2 faseskift langs x -retningen for å forskyve plasseringen av nodene og antinodene. For eksempel er den lengste bølgelengden som resonerer-den grunnleggende modusen-igjen dobbelt så lang som røret, bortsett fra at endene på røret har trykkantennoder i stedet for trykknoder. Mellom endene er det en trykknode. Når det gjelder to lukkede ender, er bølgelengden igjen begrenset til

${\ displaystyle \ lambda = {\ frac {2L} {n}},}$

${\ displaystyle n = 1,2,3, \ ldots,}$

og frekvensen er igjen begrenset til

${\ displaystyle f = {\ frac {nv} {2L}}.}$

Et Rubens -rør gir en måte å visualisere trykkvariasjonene til de stående bølgene i et rør med to lukkede ender.

2D stående bølge med en rektangulær grense

Vurder deretter tverrgående bølger som kan bevege seg langs en todimensjonal overflate innenfor en rektangulær grense med lengde L _x i x -retningen og lengde L _y i y -retningen. Eksempler på denne typen bølger er vannbølger i et basseng eller bølger på et rektangulært ark som har blitt trukket stramt. Bølgene forskyver overflaten i z -retningen, med z = 0 definert som høyden på overflaten når den er stille.

I to dimensjoner og kartesiske koordinater, den bølgeligningen er

${\ displaystyle {\ frac {\ partiell ^{2} z} {\ delvis t ^{2}}} \; = \; c ^{2} \ venstre ({\ frac {\ delvis ^{2} z} {\ delvis x^{2}}}+{\ frac {\ delvis^{2} z} {\ delvis y^{2}}} \ høyre),}$

hvor

• z ( x , y , t ) er forskyvningen av overflaten,
• c er bølgens hastighet.

For å løse denne differensialligningen, la oss først løse for Fourier -transformasjonen , med

${\ displaystyle Z (x, y, \ omega) = \ int _ {-\ infty}^{\ infty} z (x, y, t) e^{-i \ omega t} dt.}$

Tar Fourier -transformasjonen av bølgelegningen,

${\ displaystyle {\ frac {\ partiell ^{2} Z} {\ delvis x ^{2}}}+{\ frac {\ delvis ^{2} Z} {\ delvis y ^{2}}} =- {\ frac {\ omega ^{2}} {c ^{2}}} Z (x, y, \ omega).}$

Dette er et egenverdi problem der frekvensene tilsvarer egenverdier som deretter tilsvarer frekvensspesifikke moduser eller egenfunksjoner. Spesielt er dette en form for Helmholtz -ligningen, og den kan løses ved hjelp av separasjon av variabler . Anta

${\ displaystyle Z = X (x) Y (y).}$

Dele Helmholtz -ligningen med Z ,

${\ displaystyle {\ frac {1} {X (x)}} {\ frac {\ partiell ^{2} X} {\ delvis x ^{2}}}+{\ frac {1} {Y (y) }} {\ frac {\ partiell ^{2} Y} {\ delvis y ^{2}}}+{\ frac {\ omega ^{2}} {c ^{2}}} = 0.}$

Dette fører til to koblede vanlige differensialligninger. Den x sikt lik en konstant med hensyn på x som vi kan definere som

${\ displaystyle {\ frac {1} {X (x)}} {\ frac {\ partiell^{2} X} {\ delvis x^{2}}} = (ik_ {x})^{2}. }$

Løsning for X ( x ),

${\ displaystyle X (x) = A_ {k_ {x}} e^{ik_ {x} x}+B_ {k_ {x}} e^{-ik_ {x} x}.}$

Denne x -avhengigheten er sinusformet -husker Eulers formel -med konstanter A _{k x} og B _{k x} bestemt av grensebetingelsene. På samme måte tilsvarer y -termen en konstant med hensyn til y som vi kan definere som

${\ displaystyle {\ frac {1} {Y (y)}} {\ frac {\ partiell^{2} Y} {\ delvis y^{2}}} = (ik_ {y})^{2} = k_ {x}^{2}-{\ frac {\ omega^{2}} {c^{2}}},}$

og spredningsforholdet for denne bølgen er derfor

${\ displaystyle \ omega = c {\ sqrt {k_ {x}^{2}+k_ {y}^{2}}}.}$

Løse differensialligningen for y -termen,

${\ displaystyle Y (y) = C_ {k_ {y}} e^{ik_ {y} y}+D_ {k_ {y}} e^{-ik_ {y} y}.}$

Å multiplisere disse funksjonene sammen og anvende den inverse Fourier -transformasjonen, z ( x , y , t ) er en superposisjon av moduser der hver modus er et produkt av sinusformede funksjoner for x , y og t ,

${\ displaystyle z (x, y, t) \ sim e^{\ pm ik_ {x} x} e^{\ pm ik_ {y} y} e^{\ pm i \ omega t}.}$

Konstantene som bestemmer de eksakte sinusformede funksjonene, avhenger av grensebetingelsene og begynnelsesbetingelsene. For å se hvordan grensebetingelsene gjelder, kan du vurdere et eksempel som arket som er trukket stramt der z ( x , y , t ) må være null rundt den rektangulære grensen. For x -avhengigheten må z ( x , y , t ) variere på en måte at den kan være null på både x = 0 og x = L _x for alle verdier av y og t . Som i det endimensjonale eksempelet på strengen som er festet i begge ender, er den sinusformede funksjonen som tilfredsstiller denne grensetilstanden

${\ displaystyle \ sin {k_ {x} x},}$

med k _x begrenset til

${\ displaystyle k_ {x} = {\ frac {n \ pi} {L_ {x}}}, \ quad n = 1,2,3, \ dots}$

På samme måte må y -avhengigheten til z ( x , y , t ) være null både på y = 0 og y = L _y , som tilfredsstilles av

${\ displaystyle \ sin {k_ {y} y}, \ quad k_ {y} = {\ frac {m \ pi} {L_ {y}}}, \ quad m = 1,2,3, \ dots}$

Å begrense bølgetallene til disse verdiene begrenser også frekvensene som resonerer til

${\ displaystyle \ omega = c \ pi {\ sqrt {\ venstre ({\ frac {n} {L_ {x}}} \ høyre)^{2}+\ venstre ({\ frac {m} {L_ {y }}} \ høyre)^{2}}}.}$

Hvis de innledende betingelsene for z ( x , y , 0) og dets tidsderivat ż ( x , y , 0) velges slik at t -avhengigheten er en cosinus -funksjon, får stående bølger for dette systemet form

${\ displaystyle z (x, y, t) = z _ {\ text {max}} \ sin \ left ({\ frac {n \ pi x} {L_ {x}}} \ right) \ sin \ left ({ \ frac {m \ pi y} {L_ {y}}} \ right) \ cos \ left (\ omega t \ right).}$

${\ displaystyle n = 1,2,3, \ dots \ quad m = 1,2,3, \ dots}$

Så stående bølger inne i denne faste rektangulære grensen svinger i tid ved visse resonansfrekvenser parameterisert av heltallene n og m . Når de svinger i tid, reiser de ikke og deres romlige variasjon er sinusformet i både x - og y -retningene slik at de tilfredsstiller grensebetingelsene. Den grunnleggende modusen, n = 1 og m = 1 , har en enkelt antinode i midten av rektanglet. Å variere n og m gir kompliserte, men forutsigbare todimensjonale mønstre av noder og antinoder inne i rektangelet.

Legg merke til fra spredningsforholdet at forskjellige moduser - som betyr forskjellige kombinasjoner av n og m - i visse situasjoner kan resonere med samme frekvens, selv om de har forskjellige former for deres x - og y -avhengighet. For eksempel hvis grensen er firkantet, resonerer L _x = L _y , modusene n = 1 og m = 7 , n = 7 og m = 1 , og n = 5 og m = 5 alle ved

${\ displaystyle \ omega = {\ frac {c \ pi} {L_ {x}}} {\ sqrt {50}}.}$

Når vi husker at ω bestemmer egenverdien i Helmholtz -ligningen ovenfor, er antallet moduser som tilsvarer hver frekvens relatert til frekvensens mangfoldighet som en egenverdi.

Stående bølgeforhold, fase og energioverføring

Hvis de to bevegelige bevegelige bølgene ikke har samme amplitude, vil de ikke avbryte helt ved nodene, punktene der bølgene er 180 ° ute av fase, så amplituden til den stående bølgen vil ikke være null ved nodene, men bare et minimum. Standing wave ratio (SWR) er forholdet mellom amplituden ved antinoden (maksimum) og amplituden ved noden (minimum). En ren stående bølge vil ha en uendelig SWR. Den vil også ha en konstant fase når som helst i rommet (men den kan gjennomgå en 180 ° inversjon hver halve syklus). En endelig, ikke-null SWR indikerer en bølge som er delvis stasjonær og delvis beveger seg. Slike bølger kan dekomponeres til en superposisjon av to bølger: en bevegelig bølgekomponent og en stasjonær bølgekomponent. En SWR på en indikerer at bølgen ikke har en stasjonær komponent - det er rent en bevegelig bølge, siden forholdet mellom amplituder er lik 1.

En ren stående bølge overfører ikke energi fra kilden til destinasjonen. Imidlertid er bølgen fortsatt utsatt for tap i mediet. Slike tap vil manifestere seg som en endelig SWR, noe som indikerer en bevegelige bølgekomponent som forlater kilden for å levere tapene. Selv om SWR nå er endelig, kan det fortsatt være slik at ingen energi når destinasjonen fordi reisekomponenten rent utgjør tapene. I et tapsfritt medium innebærer imidlertid en endelig SWR en bestemt overføring av energi til destinasjonen.

Eksempler

Et enkelt eksempel for å forstå stående bølger er to personer som rister i hver ende av et hoppetau . Hvis de rister synkronisert, kan tauet danne et vanlig mønster av bølger som svinger opp og ned, med stasjonære punkter langs tauet der tauet er nesten stille (noder) og punkter der tauets bue er maksimal (antinoder).

Akustisk resonans

Stående bølger observeres også i fysiske medier som strenger og luftsøyler. Eventuelle bølger som beveger seg langs mediet vil reflektere tilbake når de når slutten. Denne effekten er mest merkbar i musikkinstrumenter hvor, på ulike multipler av en vibrerende streng eller luftsøyle 's egenfrekvens , blir en stående bølge er opprettet, slik at harmoniske som skal identifiseres. Noder forekommer i faste ender og anti-noder i åpne ender. Hvis den bare er festet i den ene enden, er bare oddetall harmoniske tilgjengelige. Ved den åpne ende av et rør anti-noden ikke vil være nøyaktig i enden slik den er endret ved dens kontakt med luft og så slutt korreksjon brukes for å plassere den nøyaktig. Tettheten til en streng vil påvirke frekvensen som harmoniske vil bli produsert; jo større tetthet jo lavere frekvens må være for å produsere en stående bølge med samme harmoniske.

Synlig lys

Stående bølger observeres også i optiske medier som optiske bølgeledere og optiske hulrom . Lasere bruker optiske hulrom i form av et par vendt speil, som utgjør et Fabry - Pérot interferometer . Den forsterkningsmedium i hulrommet (slik som en krystall ) avgir lys koherent , spennende stående bølger av lys i hulrommet. Lysets bølgelengde er veldig kort (i området nanometer , ^10–9 m), så de stående bølgene er mikroskopiske i størrelse. En bruk for stående lysbølger er å måle små avstander, ved hjelp av optiske leiligheter .

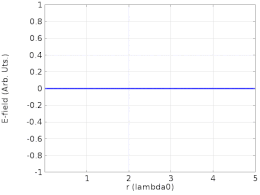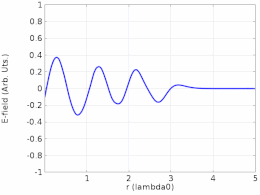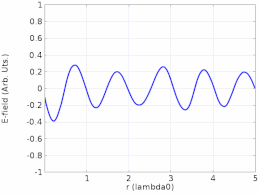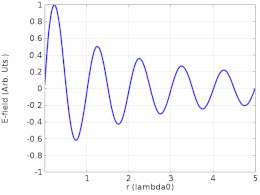
Røntgen

Forstyrrelser mellom røntgenstråler kan danne et røntgenstående bølgefelt (XSW). På grunn av den korte bølgelengden av røntgenstråler (mindre enn 1 nanometer), kan dette fenomenet utnyttes for måling av atom-skala hendelser på materialoverflater . XSW genereres i området der en røntgenstråle forstyrrer en diffraktert stråle fra en nesten perfekt enkeltkrystalloverflate eller en refleksjon fra et røntgenspeil . Ved å justere krystallgeometrien eller røntgenbølgelengden kan XSW translateres i verdensrommet og forårsake et skifte i røntgenfluorescensen eller fotoelektronutbyttet fra atomene nær overflaten. Dette skiftet kan analyseres for å finne plasseringen av en bestemt atomart i forhold til den underliggende krystallstrukturen eller speiloverflaten. XSW-metoden har blitt brukt for å tydeliggjøre atomskala-detaljene for dopemidler i halvledere, atom- og molekylær adsorpsjon på overflater og kjemiske transformasjoner involvert i katalyse .

Mekaniske bølger

Stående bølger kan mekanisk induseres til et fast medium ved hjelp av resonans. Et lettfattelig eksempel er to personer som rister i hver ende av et hoppetau. Hvis de rister synkronisert, vil tauet danne et vanlig mønster med noder og antinoder og ser ut til å være stasjonær, derav navnet stående bølge. På samme måte kan en utliggerstråle få en stående bølge pålagt den ved å påføre en grunneksitasjon. I dette tilfellet beveger den frie enden seg den største avstanden lateralt i forhold til et hvilket som helst sted langs bjelken. En slik enhet kan brukes som en sensor for å spore endringer i frekvens eller fase av fiberens resonans. En applikasjon er som måleenhet for dimensjonal metrologi .

Seismiske bølger

Stående overflatebølger på jorden observeres som frie svingninger av jorden .

Faraday bølger

Den Faraday bølge er en ikke-lineær stående bølge ved luft-væske-grenseflaten indusert av hydrodynamisk ustabilitet. Den kan brukes som en væskebasert mal for å montere mikroskala materialer.

Se også

Bølger

Elektronikk

Merknader

Referanser

• Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentals of Physics (7. utg.). John Wiley & Sons. ISBN 0-471-42959-7.
• Serway, Raymond A .; Faughn, Jerry S. (1992). College Physics (3. utg.). Saunders College Publishing. ISBN 0-03-076377-0.
• Streets, J. (2010). "Kapittel 16 - Superposisjon og stående bølger" (PDF) . Institutt for fysikk. PHYS122 Fundamentals of Physics II. University of Maryland . Hentet 23. august 2020 .

Eksterne linker

• Media relatert til Standing waves på Wikimedia Commons