Wave -funksjon - Wave function

Sammenligning av klassiske og kvanteharmoniske oscillatoroppfatninger for en enkelt spinless partikkel. De to prosessene er veldig forskjellige. Den klassiske prosessen (A – B) er representert som bevegelsen til en partikkel langs en bane. Kvanteprosessen (C – H) har ingen slik bane. Den er snarere representert som en bølge; her viser den vertikale aksen den virkelige delen (blå) og den imaginære delen (rød) av bølgefunksjonen. Paneler (C – F) viser fire forskjellige stående bølgeløsninger av Schrödinger-ligningen . Paneler (G – H) viser videre to forskjellige bølgefunksjoner som er løsninger av Schrödinger -ligningen, men ikke stående bølger.

En bølgefunksjon i kvantefysikk er en matematisk beskrivelse av kvantetilstanden i et isolert kvantesystem . Bølgefunksjonen er en kompleks verdifull sannsynlighetsamplitude , og sannsynligheten for mulige resultater av målinger gjort på systemet kan avledes av den. De vanligste symbolene for en bølgefunksjon er de greske bokstavene $ψ$ og $Ψ$ ( henholdsvis små og store psi ).

Bølgefunksjonen er en funksjon av frihetsgrader som tilsvarer et maksimalt sett med pendlende observasjoner . Når en slik representasjon er valgt, kan bølgefunksjonen være avledet fra kvantetilstanden.

For et gitt system er valget av hvilke pendlingsgrader som er fri for bruk ikke unikt, og tilsvarende er bølgefunksjonens domene heller ikke unikt. For eksempel kan det antas å være en funksjon av alle posisjonskoordinatene til partiklene over posisjonsrom, eller momenta for alle partiklene over momentum ; de to er relatert til en Fourier -transform . Noen partikler, som elektroner og fotoner , har spin uten null , og bølgefunksjonen for slike partikler inkluderer spinn som en iboende, diskret frihetsgrad; andre diskrete variabler kan også inkluderes, for eksempel isospin . Når et system har indre frihetsgrader, tildeler bølgefunksjonen ved hvert punkt i de kontinuerlige frihetsgrader (f.eks. Et punkt i rommet) et komplekst tall for hver mulig verdi av de diskrete frihetsgrader (f.eks. Z-komponent av spin)-disse verdiene vises ofte i en kolonnematrise (f.eks. en $2 \times 1$ kolonnevektor for et ikke-relativistisk elektron med spin $.mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 1 ⁄ 2$ ).

I følge superposisjonsprinsippet for kvantemekanikk kan bølgefunksjoner legges sammen og multipliseres med komplekse tall for å danne nye bølgefunksjoner og danne et Hilbert -rom . Det indre produktet mellom to bølgefunksjoner er et mål på overlappingen mellom de tilsvarende fysiske tilstandene, og brukes i den grunnleggende sannsynlighetstolkningen av kvantemekanikk, Born -regelen , som relaterer overgangssannsynligheter til indre produkter. Den Schrödingerligningen bestemmer hvor bølgefunksjoner utvikler seg over tid, og en bølgefunksjon oppfører seg kvalitativt som andre bølger , for eksempel vann-bølger eller bølger på en snor, fordi Schrödingerligningen er matematisk en type av bølgeligningen . Dette forklarer navnet "bølgefunksjon", og gir opphav til bølge -partikkeldualitet . Bølgefunksjonen i kvantemekanikken beskriver imidlertid et slags fysisk fenomen, som fortsatt er åpent for forskjellige tolkninger , som fundamentalt skiller seg fra klassiske mekaniske bølger.

I Born er statistisk tolkning i ikke-relativistisk kvantemekanikk, den kvadrerte modulus av bølgefunksjonen, $| ψ | 2$ , er et reelt tall tolket som sannsynlighetstettheten for å måle en partikkel som å være på et gitt sted - eller ha et gitt momentum - på et gitt tidspunkt, og muligens ha bestemte verdier for diskrete frihetsgrader. Integralen av denne mengden, over alle systemets frihetsgrader, må være 1 i samsvar med sannsynlighetstolkningen. Dette generelle kravet som en bølgefunksjon må tilfredsstille kalles normaliseringstilstanden . Siden bølgefunksjonen er kompleks verdsatt, kan bare den relative fasen og den relative størrelsen måles - verdien isolert sett isolert ikke forteller noe om størrelsene eller retningene til målbare observerbare ting; man må bruke kvanteoperatorer , hvis egenverdier tilsvarer sett med mulige måleresultater, på bølgefunksjonen $ψ$ og beregne de statistiske fordelingene for målbare mengder.

Historisk bakgrunn

I 1905, Albert Einstein postulerte proporsjonalitet mellom frekvensen av et foton og dens energi , , og i 1916 av det tilsvarende forholdet mellom en fotonets momentum og bølgelengde , , der er Plancks konstant . I 1923 var De Broglie den første som antydet at forholdet , nå kalt De Broglie -forholdet , holder for massive partikler, den viktigste ledetråden er Lorentz invariance , og dette kan sees på som utgangspunktet for den moderne utviklingen av kvantemekanikk. Ligningene representerer bølge -partikkeldualitet for både masseløse og massive partikler. ${\ displaystyle f}$ ${\ displaystyle E}$ ${\ displaystyle E = hf}$ ${\ displaystyle p}$ ${\ displaystyle \ lambda}$ ${\ displaystyle \ lambda = {\ frac {h} {p}}}$ $h$ ${\ displaystyle \ lambda = {\ frac {h} {p}}}$

På 1920- og 1930 -tallet ble kvantemekanikk utviklet ved hjelp av beregning og lineær algebra . De som brukte beregningsteknikkene inkluderte Louis de Broglie , Erwin Schrödinger og andre som utviklet " bølgemekanikk ". De som brukte metodene for lineær algebra inkluderte Werner Heisenberg , Max Born og andre som utviklet "matriksmekanikk". Schrödinger viste deretter at de to tilnærmingene var likeverdige.

I 1926 publiserte Schrödinger den berømte bølgelikningen som nå er oppkalt etter ham, Schrödinger -ligningen . Denne ligningen var basert på klassisk bevaring av energi ved hjelp av kvanteoperatorer og de Broglie -relasjonene, og løsningene til ligningen er bølgefunksjonene for kvantesystemet. Imidlertid var ingen klare på hvordan de skulle tolke det . Først trodde Schrödinger og andre at bølgefunksjoner representerer partikler som er spredt med det meste av partikkelen som er der bølgefunksjonen er stor. Dette viste seg å være inkompatibelt med den elastiske spredningen av en bølgepakke (som representerer en partikkel) utenfor et mål; det sprer seg i alle retninger. Selv om en spredt partikkel kan spre seg i alle retninger, bryter den ikke opp og tar av i alle retninger. I 1926 ga Born perspektivet på sannsynlighetsamplitude . Dette relaterer beregninger av kvantemekanikk direkte til sannsynlige eksperimentelle observasjoner. Det er akseptert som en del av den tolkningen av kvantemekanikk i København . Det er mange andre tolkninger av kvantemekanikk . I 1927 tok Hartree og Fock det første trinnet i et forsøk på å løse N -kroppsbølgefunksjonen , og utviklet selvkonsistenssyklusen : en iterativ algoritme for å tilnærme løsningen. Nå er den også kjent som Hartree - Fock -metoden . Den Slater determinant og varig (i en matrise ) ble en del av fremgangsmåten, gitt av John C. Slater .

Schrödinger støtte på en ligning for bølgefunksjonen som tilfredsstilte relativistisk energibesparelse før han publiserte den ikke-relativistiske, men forkastet den da den spådde negative sannsynligheter og negative energier . I 1927 fant Klein , Gordon og Fock det også, men innlemmet den elektromagnetiske interaksjonen og beviste at det var Lorentz invariant . De Broglie kom også frem til den samme ligningen i 1928. Denne relativistiske bølgelikningen er nå mest kjent som Klein - Gordon -ligningen .

I 1927 fant Pauli fenomenologisk en ikke-relativistisk ligning for å beskrive spin-1/2-partikler i elektromagnetiske felt, nå kalt Pauli-ligningen . Pauli fant at bølgefunksjonen ikke ble beskrevet av en enkelt kompleks funksjon av rom og tid, men trengte to komplekse tall, som henholdsvis tilsvarer spin +1/2 og −1/2 tilstandene til fermionen. Like etter i 1928 fant Dirac en ligning fra den første vellykkede foreningen av spesiell relativitet og kvantemekanikk som ble brukt på elektronet , nå kalt Dirac -ligningen . I dette er bølgefunksjonen en spinor representert av fire komplekse verdifulle komponenter: to for elektronet og to for elektronens antipartikkel , positronet . I den ikke-relativistiske grensen ligner Dirac-bølgefunksjonen Pauli-bølgefunksjonen for elektronet. Senere ble andre relativistiske bølgelikninger funnet.

Bølgefunksjoner og bølgelikninger i moderne teorier

Alle disse bølgelikningene er av varig betydning. Schrödinger -ligningen og Pauli -ligningen er under mange omstendigheter gode tilnærminger til de relativistiske variantene. De er betydelig lettere å løse i praktiske problemer enn de relativistiske motpartene.

Den Klein-Gordon likningen og Dirac ligningen , men som samtidig er relativistisk, ikke representerer hele avstemming av kvantemekanikk og spesiell relativitetsteori. Grenen av kvantemekanikk der disse ligningene studeres på samme måte som Schrödinger -ligningen, ofte kalt relativistisk kvantemekanikk , mens den er veldig vellykket, har sine begrensninger (se f.eks. Lamskift ) og konseptuelle problemer (se f.eks. Dirac sea ).

Relativitet gjør det uunngåelig at antall partikler i et system ikke er konstant. For full forsoning er kvantefeltteori nødvendig. I denne teorien har bølgelikningene og bølgefunksjonene sin plass, men i en noe annen form. Hovedobjektene av interesse er ikke bølgefunksjonene, men heller operatører, såkalte feltoperatører (eller bare felt der "operatør" forstås) på Hilbert -statens rom (beskrives i neste avsnitt). Det viser seg at de originale relativistiske bølgelikningene og løsningene deres fortsatt er nødvendig for å bygge Hilbert -rommet. Videre viser frie feltoperatører seg , dvs. når interaksjoner antas å ikke eksistere, (formelt) tilfredsstiller den samme ligningen som feltene (bølgefunksjonene) i mange tilfeller.

Dermed Klein-Gordon ligning (spin $0$ ) og Diraclikningen (spin $Anmeldelse for 1. / 2-$ ) i denne skikkelse forbli i teorien. Høyere rotasjons analoger innbefatter de Proca ligning (spin $1$ ), Rarita-Schwinger ligning (spin $3- / 2-$ ), og, mer generelt, den Bargmann-Wigner ligninger . For massefrie frie felt er to eksempler Maxwell -ligningen for fritt felt (spinn $1$ ) og Einstein -ligningen for det frie feltet (spinn $2$ ) for feltoperatørene. Alle er i hovedsak en direkte konsekvens av kravet om Lorentz invariance . Løsningene deres må transformeres under Lorentz -transformasjon på en foreskrevet måte, dvs. under en bestemt representasjon av Lorentz -gruppen, og det sammen med få andre rimelige krav, f.eks. Klyngedekomponeringsprinsippet , med implikasjoner for årsakssammenheng er nok til å fikse ligningene.

Dette gjelder frie feltligninger; interaksjoner er ikke inkludert. Hvis en lagrangisk tetthet (inkludert interaksjoner) er tilgjengelig, vil den lagrangiske formalismen gi en bevegelsesligning på det klassiske nivået. Denne ligningen kan være veldig kompleks og ikke lett å løse. Enhver løsning vil referere til et fast antall partikler og vil ikke redegjøre for begrepet "interaksjon" som referert til i disse teoriene, som innebærer opprettelse og utslettelse av partikler og ikke eksterne potensialer som i vanlig "første kvantisert" kvanteteori.

I strengteori er situasjonen fortsatt analog. For eksempel har en bølgefunksjon i momentumrom rollen som Fourier -ekspansjonskoeffisient i en generell tilstand av en partikkel (streng) med momentum som ikke er skarpt definert.

Definisjon (en spinnløs partikkel i en dimensjon)

Stående bølger for en partikkel i en eske , eksempler på stasjonære tilstander .

Reisende bølger av en fri partikkel.

De virkelige delene av posisjonsbølgefunksjonen

Ψ (x)

og momentbølgefunksjonen

Φ (p)

, og tilsvarende sannsynlighetstetthet

| Ψ (x) | 2

og

| Φ (p) | 2

, for en spin-0 partikkel i en

x-

eller

p-

dimensjon. Fargenes ugjennomsiktighet til partiklene tilsvarer sannsynlighetstettheten ( ikke bølgefunksjonen) for å finne partikkelen i posisjon

x

eller momentum

p

.

For nå, tenk på det enkle tilfellet av en ikke-relativistisk enkeltpartikkel, uten spinn , i en romlig dimensjon. Mer generelle saker diskuteres nedenfor.

Posisjon-mellomrom-bølgefunksjoner

Tilstanden til en slik partikkel er fullstendig beskrevet av bølgefunksjonen,

{\ displaystyle \ Psi (x, t) \ ,,}

hvor $x$ er posisjon og $t$ er tid. Dette er en kompleks verdifunksjon av to virkelige variabler $x$ og $t$ .

For en spinless partikkel i en dimensjon, hvis bølgefunksjonen blir tolket som en sannsynlighet amplitude , kvadratet modulus av bølgefunksjonen, den positivt reelt tall

{\ displaystyle \ left | \ Psi (x, t) \ right | ^{2} = \ Psi ^{*} (x, t) \ Psi (x, t) = \ rho (x, t),}

tolkes som sannsynlighetstettheten for at partikkelen er på $x$ . Stjernen indikerer det komplekse konjugatet . Hvis partikkelens posisjon måles , kan plasseringen ikke bestemmes ut fra bølgefunksjonen, men beskrives ved en sannsynlighetsfordeling .

Normaliseringstilstand

Sannsynligheten for at posisjonen $x$ vil være i intervallet $a \leq x \leq b$ er integralet av tettheten over dette intervallet:

{\ displaystyle P_ {a \ leq x \ leq b} (t) = \ int _ {a}^{b} \, | \ Psi (x, t) |^{2} dx}

hvor $t$ er tidspunktet da partikkelen ble målt. Dette fører til normaliseringstilstanden :

{\ displaystyle \, \ int _ {-\ infty}^{\ infty} \, | \ Psi (x, t) |^{2} dx = 1 \ ,,}

fordi hvis partikkelen måles, er det 100% sannsynlighet for at den vil være et sted .

For et gitt system danner settet med alle mulige normaliserbare bølgefunksjoner (til enhver tid) et abstrakt matematisk vektorrom , noe som betyr at det er mulig å legge sammen forskjellige bølgefunksjoner og multiplisere bølgefunksjoner med komplekse tall (se vektorrom for detaljer). Teknisk, på grunn av normaliseringstilstanden, danner bølgefunksjoner et projektivt rom i stedet for et vanlig vektorrom. Dette vektorrommet er uendelig- dimensjonalt , fordi det ikke er noe endelig sett med funksjoner som kan legges sammen i forskjellige kombinasjoner for å lage alle mulige funksjoner. Det er også et Hilbert -rom , fordi det indre produktet av to bølgefunksjoner $Ψ 1$ og $Ψ 2$ kan defineres som det komplekse tallet (på tidspunktet $t$ )

{\ displaystyle (\ Psi _ {1}, \ Psi _ {2}) = \ int _ {-\ infty}^{\ infty} \, \ Psi _ {1}^{*} (x, t) \ Psi _ {2} (x, t) dx.}

Flere detaljer er gitt nedenfor . Selv om det indre produktet av to bølgefunksjoner er et komplekst tall, er det indre produktet av en bølgefunksjon $Ψ$ med seg selv,

{\ displaystyle (\ Psi, \ Psi) = \ | \ Psi \ |^{2} \ ,,}

er alltid et positivt reelt tall. Tallet $|| Ψ ||$ (ikke $|| Ψ || 2$ ) kalles normen for bølgefunksjonen $Ψ$ .

Hvis $(Ψ, Ψ) = 1$ , er $Ψ$ normalisert. Hvis $Ψ$ ikke er normalisert, gir divisjonen med normen den normaliserte funksjonen $Ψ/|| Ψ ||$ . To bølgefunksjoner $Ψ 1$ og $Ψ 2$ er ortogonale hvis $(Ψ 1, Ψ 2) = 0$ . Hvis de er normaliserte og ortogonale, er de ortonormale . Ortogonalitet (derav også ortonormalitet) av bølgefunksjoner er ikke en nødvendig betingelse bølgefunksjoner må tilfredsstille, men er lærerikt å ta hensyn til siden dette garanterer lineær uavhengighet av funksjonene. I en lineær kombinasjon av ortogonale bølgefunksjoner $Ψ n har$ vi,

{\ displaystyle \ Psi = \ sum _ {n} a_ {n} \ Psi _ {n} \ ,, \ quad a_ {n} = {\ frac {(\ Psi _ {n}, \ Psi)} {( \ Psi _ {n}, \ Psi _ {n})}}}}

Dersom de bølgefunksjoner $y n$ var nonorthogonal, vil koeffisientene være mindre lett å få tak i.

Kvantetilstander som vektorer

I tolkningen i København gir modulen i kvadratet til det indre produktet (et komplekst tall) et reelt tall

{\ displaystyle \ left | (\ Psi _ {1}, \ Psi _ {2}) \ right |^{2} = P \ left (\ Psi _ {2} \ rightarrow \ Psi _ {1} \ right) \ ,,}

som, forutsatt at begge bølgefunksjoner er normalisert, blir tolket som sannsynligheten for bølgefunksjonen $Ψ 2$ "skjuling" av den nye bølgefunksjonen $Ψ en$ ved måling av et observerbart, hvis egenverdier er de mulige resultatene av målingen, med $Ψ 1$ vesen en egenvektor av den resulterende egenverdien. Dette er Born -regelen , og er et av de grunnleggende postulatene for kvantemekanikk.

På et bestemt tidspunkt er alle verdiene til bølgefunksjonen $Ψ (x, t)$ komponenter i en vektor. Det er uendelig mange av dem, og integrasjon brukes i stedet for summering. I Bra -ket -notasjon er denne vektoren skrevet

{\ displaystyle | \ Psi (t) \ rangle = \ int \ Psi (x, t) | x \ rangle dx}

og blir referert til som en "kvantetilstandsvektor", eller ganske enkelt "kvantetilstand". Det er flere fordeler med å forstå bølgefunksjoner som representerende elementer i et abstrakt vektorrom:

Alle de kraftige verktøyene til lineær algebra kan brukes til å manipulere og forstå bølgefunksjoner. For eksempel:
- Lineær algebra forklarer hvordan et vektorrom kan gis et grunnlag , og deretter kan en hvilken som helst vektor i vektorrommet uttrykkes på dette grunnlaget. Dette forklarer forholdet mellom en bølgefunksjon i posisjonsrom og en bølgefunksjon i momentum og antyder at det også er andre muligheter.
- Bra -ket -notasjon kan brukes til å manipulere bølgefunksjoner.
Ideen om at kvantetilstander er vektorer i et abstrakt vektorrom er helt generelt i alle aspekter av kvantemekanikk og kvantefeltteori , mens ideen om at kvantetilstander er kompleks-verdsatte "bølgefunksjoner" i rommet bare er sann i visse situasjoner.

Tidsparameteren undertrykkes ofte, og vil være i det følgende. Den $x$ koordinaten er en kontinuerlig indeks. Den $| x ⟩$ er basisvektorene, som er ortonormal slik at deres indre produkt er en deltafunksjon ;

{\ displaystyle \ langle x '| x \ rangle = \ delta (x'-x)}

og dermed

{\ displaystyle \ langle x '| \ Psi \ rangle = \ int \ Psi (x) \ langle x' | x \ rangle dx = \ Psi (x ')}

og

{\ displaystyle | \ Psi \ rangle = \ int | x \ rangle \ langle x | \ Psi \ rangle dx = \ left (\ int | x \ rangle \ langle x | dx \ right) | \ Psi \ rangle}

som belyser identitetsoperatøren

{\ displaystyle I = \ int | x \ rangle \ langle x | dx \ ,.}

Ved å finne identitetsoperatøren på et grunnlag kan den abstrakte tilstanden uttrykkes eksplisitt på et grunnlag, og mer (det indre produktet mellom to tilstandsvektorer og andre operatører for observerbare ting kan uttrykkes i grunnlaget).

Momentum-space bølgefunksjoner

Partikkelen har også en bølgefunksjon i momentum :

{\ displaystyle \ Phi (p, t)}

hvor $p$ er momentum i en dimensjon, som kan være hvilken som helst verdi fra $-\infty$ til $+\infty$ , og $t$ er tid.

Analogt med posisjonstilfellet kan det indre produktet av to bølgefunksjoner $Φ 1 (p, t)$ og $Φ 2 (p, t)$ defineres som:

{\ displaystyle (\ Phi _ {1}, \ Phi _ {2}) = \ int _ {-\ infty}^{\ infty} \, \ Phi _ {1}^{*} (p, t) \ Phi _ {2} (p, t) dp \ ,.}

En spesiell løsning på den tidsuavhengige Schrödinger-ligningen er

{\ displaystyle \ Psi _ {p} (x) = e^{ipx/\ hbar},}

en plan bølge , som kan brukes i beskrivelsen av en partikkel med momentum nøyaktig $p$ , siden det er en egenfunksjon av momentoperatoren. Disse funksjonene er ikke normaliserbare til enhet (de er ikke firkant-integrerbare), så de er egentlig ikke elementer av fysisk Hilbert-rom. Settet

{\ displaystyle \ {\ Psi _ {p} (x, t),-\ infty \ leq p \ leq \ infty \}}

danner det som kalles momentum -grunnlaget . Dette "grunnlaget" er ikke et grunnlag i vanlig matematisk forstand. For det første, siden funksjonene ikke er normaliserbare, blir de i stedet normalisert til en deltafunksjon ,

{\ displaystyle (\ Psi _ {p}, \ Psi _ {p '}) = \ delta (p-p').}

For en annen ting, selv om de er lineært uavhengige, er det for mange av dem (de danner et utallig sett) til grunnlag for fysisk Hilbert -rom. De kan fortsatt brukes til å uttrykke alle funksjoner i den ved å bruke Fourier -transformasjoner som beskrevet nedenfor.

Forholdet mellom posisjon og momentum representasjoner

De $x$ og $p$ representasjoner er

{\ displaystyle {\ begin {align} | \ Psi \ rangle = I | \ Psi \ rangle & = \ int | x \ rangle \ langle x | \ Psi \ rangle dx = \ int \ Psi (x) | x \ rangle dx, \\ | \ Psi \ rangle = I | \ Psi \ rangle & = \ int | p \ rangle \ langle p | \ Psi \ rangle dp = \ int \ Phi (p) | p \ rangle dp. \ end { justert}}}

Ta nå projeksjonen av tilstanden $Ψ$ på momentums egenfunksjoner ved å bruke det siste uttrykket i de to ligningene,

{\ displaystyle \ int \ Psi (x) \ langle p | x \ rangle dx = \ int \ Phi (p ') \ langle p | p' \ rangle dp '= \ int \ Phi (p') \ delta (p -p ') dp' = \ Phi (p).}

Deretter bruker du det kjente uttrykket for passende normaliserte egenstater i momentum i posisjonsrepresentasjonsløsningene til den gratis Schrödinger -ligningen

{\ displaystyle \ langle x | p \ rangle = p (x) = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} e^{{\ frac {i} {\ hbar}} px} \ Rightarrow \ langle p | x \ rangle = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} e^{-{\ frac {i} {\ hbar}} px},}

man får

{\ displaystyle \ Phi (p) = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} \ int \ Psi (x) e^{-{\ frac {i} {\ hbar}} px } dx \ ,.}

På samme måte ved å bruke posisjons egenfunksjoner,

{\ displaystyle \ Psi (x) = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} \ int \ Phi (p) e^{{\ frac {i} {\ hbar}} px} dp \ ,.}

Posisjons-rom og momentum-rom bølgefunksjoner er således funnet å være Fourier-transformasjoner av hverandre. De to bølgefunksjonene inneholder den samme informasjonen, og enten en alene er tilstrekkelig til å beregne hvilken som helst egenskap av partikkelen. Som representanter for elementer i det abstrakte fysiske Hilbert-rommet, hvis elementer er de mulige tilstandene i systemet som vurderes, representerer de den samme tilstandsvektoren, derav identiske fysiske tilstander , men de er generelt sett ikke like når de blir sett på som kvadratintegrerbare funksjoner.

I praksis brukes posisjon-rom-bølgefunksjonen mye oftere enn momentum-rom-bølgefunksjonen. Potensialet som går inn i den relevante ligningen (Schrödinger, Dirac, etc.) bestemmer på hvilket grunnlag beskrivelsen er lettest. For harmonisk oscillator , $x$ og $p$ angi symmetrisk, slik at det ikke spiller det ingen rolle hvilken beskrivelse man bruker. Den samme ligningen (modulokonstanter) resulterer. Fra dette følger, med litt ettertanke, en faktoid: Løsningene på bølgelikningen til den harmoniske oscillatoren er egenfunksjoner av Fourier -transformasjonen i $L 2$ .

Definisjoner (andre tilfeller)

Følgende er de generelle formene for bølgefunksjonen for systemer i høyere dimensjoner og flere partikler, samt inkluderer andre frihetsgrader enn posisjonskoordinater eller momentkomponenter.

Enpartikkeltilstander i 3d posisjonsrom

Posisjon-rom-bølgefunksjonen til en enkelt partikkel uten spinn i tre romlige dimensjoner ligner tilfellet med en romlig dimensjon ovenfor:

{\ displaystyle \ Psi (\ mathbf {r}, t)}

hvor $r$ er posisjonsvektoren i det tredimensjonale rommet, og $t$ er tiden. Som alltid $Ψ (r, t)$ er en kompleks verdifunksjon av reelle variabler. Som en enkelt vektor i Dirac -notasjon

{\ displaystyle | \ Psi (t) \ rangle = \ int d^{3} \! \ mathbf {r} \, \ Psi (\ mathbf {r}, t) \, | \ mathbf {r} \ rangle}

Alle de tidligere merknadene om indre produkter, momentum -rombølgefunksjoner, Fourier -transformasjoner og så videre strekker seg til høyere dimensjoner.

For en partikkel med spinn , som ignorerer plasseringsfrihetsgrader, er bølgefunksjonen en funksjon av bare spinn (tid er en parameter);

{\ displaystyle \ xi (s_ {z}, t)}

hvor $s z$ er spinnprojeksjonens kvantetall langs $z$ -aksen. ( $Z$ -aksen er et vilkårlig valg; andre akser kan i stedet brukes hvis bølgefunksjonen transformeres på riktig måte, se nedenfor.) $S z$ -parameteren, i motsetning til $r$ og $t$ , er en diskret variabel . For eksempel, for en spin-1/2- partikkel kan $s z$ bare være $+1/2$ eller $-1/2$ , og ikke noen annen verdi. (Generelt, for spinn $s$ , kan $s z$ være $s, s - 1,\dots, - s + 1, - s$ ). Å sette inn hvert kvantetall gir en kompleks verdifull funksjon av rom og tid, det er $2 s + 1$ av dem. Disse kan ordnes i en kolonnevektor

{\ displaystyle {\ xi = {\ begin {bmatrix} \ xi (s, t) \\\ xi (s-1, t) \\\ vdots \\\ xi (-(s-1), t) \ \\ xi (-s, t) \\\ end {bmatrix}} = \ xi (s, t) {\ begin {bmatrix} 1 \\ 0 \\\ vdots \\ 0 \\ 0 \\\ end { bmatrix}}+\ xi (s-1, t) {\ begin {bmatrix} 0 \\ 1 \\\ vdots \\ 0 \\ 0 \\\ end {bmatrix}}+\ cdots+\ xi (-( s-1), t) {\ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 1 \\ 0 \\\ end {bmatrix}}+\ xi (-s, t) {\ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ 1 \\\ end {bmatrix}}}}

I bra -ket -notasjon ordnes disse lett inn i komponentene i en vektor

{\ displaystyle | \ xi (t) \ rangle = \ sum _ {s_ {z} =-s}^{s} \ xi (s_ {z}, t) \, | s_ {z} \ rangle}

Hele vektoren $ξ$ er en løsning av Schrödinger -ligningen (med en passende Hamiltonian), som utspiller seg til et koblet system med $2 s + 1$ vanlige differensialligninger med løsninger $ξ (s, t), ξ (s - 1, t), \dots, Ξ ( - s, t)$ . Begrepet "spinnfunksjon" i stedet for "bølgefunksjon" brukes av noen forfattere. Dette kontrasterer løsningene for posisjonering av rombølgefunksjoner, posisjonskoordinatene er kontinuerlige frihetsgrader, for da tar Schrödinger -ligningen formen av en bølgeligning.

Mer generelt, for en partikkel i 3d med et hvilket som helst spinn, kan bølgefunksjonen skrives i "posisjon - spinnrom" som:

{\ displaystyle \ Psi (\ mathbf {r}, s_ {z}, t)}

og disse kan også ordnes i en kolonnevektor

{\ displaystyle \ Psi (\ mathbf {r}, t) = {\ begin {bmatrix} \ Psi (\ mathbf {r}, s, t) \\\ Psi (\ mathbf {r}, s-1, t ) \\\ vdots \\\ Psi (\ mathbf {r},-(s-1), t) \\\ Psi (\ mathbf {r}, -s, t) \\\ end {bmatrix}}}

der spinneavhengigheten er plassert i indeksering av oppføringene, og bølgefunksjonen er en kompleks vektor-verdsatt funksjon av rom og tid.

Alle verdier for bølgefunksjonen, ikke bare for diskrete, men kontinuerlige variabler, samles også til en enkelt vektor

{\ displaystyle | \ Psi (t) \ rangle = \ sum _ {s_ {z}} \ int d^{3} \! \ mathbf {r} \, \ Psi (\ mathbf {r}, s_ {z} , t) \, | \ mathbf {r}, s_ {z} \ rangle}

For en enkelt partikkel, tensorproduktet $\otimes$ av sin posisjonstilstandsvektor $| y ⟩$ og spinntilstand vektor $| ξ ⟩$ gir det sammensatte posisjonsspinntilstand vektor

{\ displaystyle | \ psi (t) \ rangle \! \ otimes \! | \ xi (t) \ rangle = \ sum _ {s_ {z}} \ int d^{3} \! \ mathbf {r} \ , \ psi (\ mathbf {r}, t) \, \ xi (s_ {z}, t) \, | \ mathbf {r} \ rangle \! \ otimes \! | s_ {z} \ rangle}

med identifikasjonene

{\ displaystyle | \ Psi (t) \ rangle = | \ psi (t) \ rangle \! \ otimes \! | \ xi (t) \ rangle}

{\ displaystyle \ Psi (\ mathbf {r}, s_ {z}, t) = \ psi (\ mathbf {r}, t) \, \ xi (s_ {z}, t)}

{\ displaystyle | \ mathbf {r}, s_ {z} \ rangle = | \ mathbf {r} \ rangle \! \ otimes \! | s_ {z} \ rangle}

Tensorproduktfaktoriseringen er bare mulig hvis partikkelens orbital- og spinnvinkelmoment er separerbare i den hamiltonske operatøren som ligger til grunn for systemets dynamikk (med andre ord kan Hamiltonian deles inn i summen av orbitale og spinntermer). Tidsavhengigheten kan plasseres i begge faktorene, og tidsutviklingen for hver enkelt kan studeres separat. Faktoriseringen er ikke mulig for de interaksjonene der et eksternt felt eller en plassavhengig mengde kobler seg til spinnet; eksempler inkluderer en partikkel i et magnetfelt , og spin -orbit -kobling .

Den foregående diskusjonen er ikke begrenset til spinn som en diskret variabel, den totale vinkelmoment J kan også brukes. Andre diskrete frihetsgrader, som isospin , kan uttrykkes på samme måte som spin ovenfor.

Mange partikkeltilstander i 3d posisjonsrom

Reisende bølger av to frie partikler, med to av tre dimensjoner undertrykt. Øverst er posisjon-rom-bølgefunksjon, bunn er momentum-rom-bølgefunksjon, med tilsvarende sannsynlighetstetthet.

Hvis det er mange partikler, er det generelt bare en bølgefunksjon, ikke en egen bølgefunksjon for hver partikkel. Det faktum at en bølgefunksjon beskriver mange partikler er det som gjør kvantefiltring og EPR -paradokset mulig. Posisjon-rom-bølgefunksjonen for $N-$ partikler er skrevet:

{\ displaystyle \ Psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2} \ cdots \ mathbf {r} _ {N}, t)}

hvor $r i$ er posisjonen til den $i$ partikkelen i det tredimensjonale rommet, og $t$ er tiden. Til sammen er dette en kompleks verdifunksjon av $3 N + 1$ reelle variabler.

I kvantemekanikken er det et grunnleggende skille mellom identiske partikler og skillbare partikler. For eksempel er alle to elektroner identiske og grunnleggende ikke skillbare fra hverandre; fysikklovene gjør det umulig å "stemple et identifikasjonsnummer" på et bestemt elektron for å holde styr på det. Dette oversetter til et krav om bølgefunksjonen for et system med identiske partikler:

{\ displaystyle \ Psi \ left (\ ldots \ mathbf {r} _ {a}, \ ldots, \ mathbf {r} _ {b}, \ ldots \ right) = \ pm \ Psi \ left (\ ldots \ mathbf {r} _ {b}, \ ldots, \ mathbf {r} _ {a}, \ ldots \ right)}

der $+$ -tegnet oppstår hvis partiklene er alle bosoner og $-$ tegn hvis de alle er fermioner . Med andre ord er bølgefunksjonen enten totalt symmetrisk i posisjonene til bosoner, eller helt antisymmetrisk i posisjonene til fermioner. Den fysiske utvekslingen av partikler tilsvarer matematisk bytte av argumenter i bølgefunksjonen. Antisymmetrifunksjonen til fermioniske bølgefunksjoner fører til Pauli -prinsippet . Generelt er bosoniske og fermioniske symmetri krav manifestasjon av partikkelstatistikk og er tilstede i andre kvantetilstandsformalismer.

For $N$ skillbare partikler (ingen to er identiske , dvs. ingen to som har samme sett med kvantetall), er det ikke noe krav om at bølgefunksjonen skal være enten symmetrisk eller antisymmetrisk.

For en samling partikler, noen identiske med koordinatene $r 1, r 2, ...$ og andre som kan skilles $x 1, x 2, ...$ (ikke identiske med hverandre, og ikke identiske med de ovennevnte identiske partiklene), bølgen funksjonen er symmetrisk eller antisymmetrisk i de samme partikkelkoordinatene $r i$ :

{\ displaystyle \ Psi \ left (\ ldots \ mathbf {r} _ {a}, \ ldots, \ mathbf {r} _ {b}, \ ldots, \ mathbf {x} _ {1}, \ mathbf {x } _ {2}, \ ldots \ right) = \ pm \ Psi \ left (\ ldots \ mathbf {r} _ {b}, \ ldots, \ mathbf {r} _ {a}, \ ldots, \ mathbf { x} _ {1}, \ mathbf {x} _ {2}, \ ldots \ right)}

Igjen er det ikke noe symmetri -krav for de skillbare partikkelkoordinatene $x i$ .

Bølgefunksjonen for N- partikler hver med spinn er den komplekse verdifunksjonen

{\ displaystyle \ Psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1}, s_ {z \, 2} \ cdots s_ {z \, N}, t)}

Samler alle disse komponentene til en enkelt vektor,

{\ displaystyle \ underbrace {| \ Psi \ rangle} _ {\ text {state vector (ket)}} = \ underbrace {\ overbrace {\ sum _ {s_ {z \, 1}, \ ldots, s_ {z \ , N}}} ^{\ text {diskrete etiketter}} \ overbrace {\ int \ limit \ limits _ {R_ {N}} d ^{3} \ mathbf {r} _ {N} \ cdots \ int \ limits \ limit _ {R_ {1}} d ^{3} \ mathbf {r} _ {1}} ^{\ text {sammenhengende etiketter}}} _ {\ text {legger opp}} \, \ underbrace {{\ \ Psi} (\ mathbf {r} _ {1}, \ ldots, \ mathbf {r} _ {N}, s_ {z \, 1}, \ ldots, s_ {z \, N})} _ {\ text {bølgefunksjon (komponent av tilstandsvektor langs basisstatus)}} \ underbrace {| \ mathbf {r} _ {1}, \ ldots, \ mathbf {r} _ {N}, s_ {z \, 1}, \ ldots, s_ {z \, N} \ rangle} _ {\ text {basis state (basis ket)}} \ ,.}

For identiske partikler gjelder symmetri -krav for både posisjons- og spinnargumenter for bølgefunksjonen, så den har den generelle korrekte symmetrien.

Formlene for de indre produktene er integraler over alle koordinater eller momenta og summer over alle spinnkvantetall. For det generelle tilfellet av $N$ -partikler med spinn i 3d,

{\ displaystyle (\ Psi _ {1}, \ Psi _ {2}) = \ sum _ {s_ {z \, N}} \ cdots \ sum _ {s_ {z \, 2}} \ sum _ {s_ {z \, 1}} \ int \ limit _ {\ mathrm {all \, space}} d^{3} \ mathbf {r} _ {1} \ int \ limit _ {\ mathrm {all \, space} } d^{3} \ mathbf {r} _ {2} \ cdots \ int \ limit _ {\ mathrm {all \, space}} d^{3} \ mathbf {r} _ {N} \ Psi _ { 1}^{*} \ venstre (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ right ) \ Psi _ {2} \ venstre (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ Ikke sant)}

dette er totalt $N$ tredimensjonale volumintegraler og $N-$ summer over spinnene. Differensialvolumelementene $d 3 r i$ er også skrevet " $dV i$ " eller " $dx i dy i dz i$ ".

De flerdimensjonale Fourier -transformasjonene av posisjonen eller posisjonen - spinn mellomromsbølgefunksjoner gir momentum eller momentum - spinn rombølgefunksjoner.

Sannsynlighetstolkning

For det generelle tilfellet av $N$ -partikler med spinn i 3d, hvis $Ψ$ tolkes som en sannsynlighetsamplitude, er sannsynlighetstettheten

{\ displaystyle \ rho \ left (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ right) = \ venstre | \ Psi \ venstre (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ right ) \ høyre |^{2}}

og sannsynligheten for at partikkelen er i en region $R en$ med sentrifuge $s z 1 = m 1$ og partikkel 2 er i region $R 2$ sammen med spinn $r z 2 = m 2$ etc. ved tidspunktet $t$ er integralet av sannsynlighetstettheten over disse regionene og evaluert på disse spinnnumrene:

{\ displaystyle P _ {\ mathbf {r} _ {1} \ i R_ {1}, s_ {z \, 1} = m_ {1}, \ ldots, \ mathbf {r} _ {N} \ i R_ { N}, s_ {z \, N} = m_ {N}} (t) = \ int \ limit _ {R_ {1}} d^{3} \ mathbf {r} _ {1} \ int \ limit _ {R_ {2}} d^{3} \ mathbf {r} _ {2} \ cdots \ int \ limit _ {R_ {N}} d^{3} \ mathbf {r} _ {N} \ venstre | \ Psi \ venstre (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, m_ {1} \ cdots m_ {N}, t \ right) \ right |^{2}}

Tidsavhengighet

For systemer med tidsuavhengige potensialer kan bølgefunksjonen alltid skrives som en funksjon av frihetsgrader multiplisert med en tidsavhengig fasefaktor, hvis form er gitt av Schrödinger-ligningen. For $N$ -partikler, bare vurderer posisjonene sine og undertrykker andre frihetsgrader,

{\ displaystyle \ Psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2}, \ ldots, \ mathbf {r} _ {N}, t) = e^{-iEt/\ hbar } \, \ psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2}, \ ldots, \ mathbf {r} _ {N}) \ ,,}

hvor $E$ er energiens egenverdi i systemet som tilsvarer egenstaten $Ψ$ . Bølgefunksjoner i denne formen kalles stasjonære tilstander .

Tidsavhengigheten til kvantetilstanden og operatørene kan plasseres i henhold til enhetstransformasjoner på operatørene og tilstandene. For enhver kvantetilstand $| Ψ⟩$ og operator $O$ , i Schrödinger -bildet $| Ψ (t)⟩$ endres med tiden i henhold til Schrödinger -ligningen mens $O$ er konstant. I Heisenberg -bildet er det omvendt, $| Ψ⟩$ er konstant mens $O (t)$ utvikler seg med tiden i henhold til Heisenberg -bevegelsesligningen. Dirac -bildet (eller interaksjonen) er mellomliggende, tidsavhengighet er steder i både operatører og tilstander som utvikler seg i henhold til bevegelsesligninger. Det er først og fremst nyttig ved beregning av S-matriseelementer .

Ikke-relativistiske eksempler

Følgende er løsninger på Schrödinger -ligningen for en ikke -relativistisk spinless partikkel.

Endelig potensiell barriere

Spredning ved en begrenset potensiell barriere i høyde

V 0

. Amplituder og retning for venstre og høyre bevegelige bølger er angitt. I rødt, de bølgene som brukes til avledning av refleksjonen og overføringsamplituden.

E > V 0

for denne illustrasjonen.

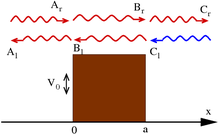
Et av de mest fremtredende trekk ved bølgemekanikken er en mulighet for at en partikkel kan nå et sted med et uoverkommelig (i klassisk mekanikk) kraftpotensial . En vanlig modell er " potensialbarrieren ", den endimensjonale saken har potensial

{\ displaystyle V (x) = {\ begin {cases} V_ {0} & | x | <a \\ 0 & | x | \ geq a \ end {cases}}}

og steady-state-løsningene til bølgelikningen har formen (for noen konstanter $k, κ$ )

{\ displaystyle \ Psi (x) = {\ begin {cases} A _ {\ mathrm {r}} e^{ikx}+A _ {\ mathrm {l}} e^{-ikx} & x <-a, \\ B _ {\ mathrm {r}} e^{\ kappa x}+B _ {\ mathrm {l}} e^{-\ kappa x} & | x | \ leq a, \\ C _ {\ mathrm {r}} e^{ikx}+C _ {\ mathrm {l}} e^{-ikx} & x> a. \ end {cases}}}

Vær oppmerksom på at disse bølgefunksjonene ikke er normaliserte; se spredningsteori for diskusjon.

Standardtolkningen av dette er som en strøm av partikler som avfyres på trinnet fra venstre (retningen til negative $x$ ): innstilling $A r = 1$ tilsvarer avfyring av partikler enkeltvis; begrepene som inneholder $A r$ og $C r$ betyr bevegelse til høyre, mens $A l$ og $C l$ - til venstre. Under denne bjelke tolkning, satt $C l = 0$ da noen partikler kommer fra høyre. Ved å anvende kontinuiteten til bølgefunksjoner og deres derivater ved grensene, er det derfor mulig å bestemme konstantene ovenfor.

3D begrenset elektronbølge fungerer i en kvantepunkt. Her vises rektangulære og trekantformede kvantepunkter. Energitilstander i rektangulære prikker er mer s-type og p-type . I en trekantet prikk blandes bølgefunksjonene imidlertid på grunn av innesperringssymmetri. (Klikk for animasjon)

I en halvleder krystallitt hvis radius er mindre enn størrelsen av dens exciton Bohr radius , blir eksitoner presset, noe som fører til Quantum innesperring . Energinivåene kan deretter modelleres ved hjelp av partikkelen i en boksmodell der energien i forskjellige tilstander er avhengig av eskens lengde.

Kvant harmonisk oscillator

Bølgefunksjonene for den kvanteharmoniske oscillatoren kan uttrykkes i form av eremittpolynomer $H n$ , de er

{\ displaystyle \ Psi _ {n} (x) = {\ sqrt {\ frac {1} {2^{n} \, n!}}} \ cdot \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ høyre)^{1/4} \ cdot e^{-{\ frac {m \ omega x^{2}} {2 \ hbar}}} \ cdot H_ {n} \ venstre ({ \ sqrt {\ frac {m \ omega} {\ hbar}}} x \ høyre)}

hvor $n = 0, 1, 2,\dots$ .

Elektronsannsynlighetstettheten for de første få hydrogenatom elektron orbitaler vist som tverrsnitt. Disse orbitalene danner et ortonormalt grunnlag for elektronens bølgefunksjon. Ulike orbitaler er avbildet med ulik skala.

Hydrogenatom

Bølgefunksjonene til et elektron i et hydrogenatom uttrykkes i form av sfæriske harmoniske og generaliserte Laguerre -polynomer (disse er definert annerledes av forskjellige forfattere - se hovedartikkelen om dem og hydrogenatomet).

Det er praktisk å bruke sfæriske koordinater, og bølgefunksjonen kan skilles i funksjoner for hver koordinat,

{\ displaystyle \ Psi _ {n \ ell m} (r, \ theta, \ phi) = R (r) \, \, Y _ {\ ell}^{m} \! (\ theta, \ phi)}

hvor $R$ er radielle funksjoner og $Y m ℓ (θ, φ)$ er sfæriske harmoniske grader $ℓ$ og rekkefølge $m$ . Dette er det eneste atomet som Schrödinger -ligningen har blitt løst nøyaktig. Flerelektronatomer krever tilnærmede metoder. Familien av løsninger er:

{\ displaystyle \ Psi _ {n \ ell m} (r, \ theta, \ phi) = {\ sqrt {{\ left ({\ frac {2} {na_ {0}}} \ right)}^{3 } {\ frac {(n- \ ell -1)!} {2n [(n+\ ell)!]}}}} e^{-r/na_ {0}} \ venstre ({\ frac {2r} { na_ {0}}} \ høyre)^{\ ell} L_ {n- \ ell -1}^{2 \ ell +1} \ venstre ({\ frac {2r} {na_ {0}}} \ høyre) \ cdot Y _ {\ ell}^{m} (\ theta, \ phi)}

hvor $en 0 = 4 πε 0 ħ 2 / m e e 2$ er Bohr -radius , $L 2 ℓ + 1 n - ℓ - 1$ er de generaliserte Laguerre -polynomene av grad $n - ℓ - 1$ , $n = 1, 2, ...$ er det viktigste kvantetallet , $ℓ = 0, 1, ... n - 1$ det azimutale kvantetallet , $m = - ℓ, - ℓ + 1, ..., ℓ - 1, ℓ$ det magnetiske kvantetallet . Hydrogenlignende atomer har svært like løsninger.

Denne løsningen tar ikke hensyn til elektronens spinn.

I figuren av hydrogenorbitalene er de 19 delbildene bilder av bølgefunksjoner i posisjonsrom (normen i kvadrat). Bølgefunksjonene representerer den abstrakte tilstanden preget av trippel kvantetall $(n, l, m)$ , nederst til høyre på hvert bilde. Dette er det viktigste kvantetallet, det orbitale vinkelmomentet og det magnetiske kvantetallet. Sammen med ett spinnprojeksjonskvantum av elektronet, er dette et komplett sett med observerbare.

Figuren kan tjene til å illustrere noen ytterligere egenskaper ved funksjonsrommene til bølgefunksjoner.

I dette tilfellet er bølgefunksjonene firkantet integrerbare. Man kan i utgangspunktet ta funksjonsrommet som rommet til firkantede integrerbare funksjoner, vanligvis betegnet $L 2$ .
De viste funksjonene er løsninger på Schrödinger -ligningen. Det er åpenbart at ikke alle funksjoner i $L 2$ tilfredsstiller Schrödinger -ligningen for hydrogenatomet. Funksjonsrommet er dermed et underrom av $L 2$ .
De viste funksjonene er en del av et grunnlag for funksjonsområdet. For hver trippel $(n, l, m)$ tilsvarer det en basisbølgefunksjon. Hvis det tas hensyn til spinn, er det to basisfunksjoner for hver trippel. Funksjonsrommet har dermed et tellbart grunnlag .
Basisfunksjonene er gjensidig ortonormale .

Bølgefunksjoner og funksjonsrom

Begrepet funksjonsrom kommer naturlig inn i diskusjonen om bølgefunksjoner. Et funksjonsrom er et sett med funksjoner, vanligvis med noen definerende krav til funksjonene (i det foreliggende tilfellet at de er firkantet integrerbare ), noen ganger med en algebraisk struktur på settet (i dette tilfellet en vektorromstruktur med et indre produkt ), sammen med en topologi på settet. Sistnevnte vil bli sparsomt brukt her, det er bare nødvendig for å få en presis definisjon av hva det betyr for at et delsett av et funksjonsrom skal lukkes . Det vil bli konkludert nedenfor at funksjonsrommet til bølgefunksjoner er et Hilbert -rom . Denne observasjonen er grunnlaget for den dominerende matematiske formuleringen av kvantemekanikk.

Vector plass struktur

En bølgefunksjon er et element i et funksjonsrom delvis preget av følgende konkrete og abstrakte beskrivelser.

Schrödinger -ligningen er lineær. Dette betyr at løsningene på det, bølgefunksjoner, kan legges til og multipliseres med skalarer for å danne en ny løsning. Settet med løsninger på Schrödinger -ligningen er et vektorrom.
Superposisjonsprinsippet for kvantemekanikk. Hvis $Ψ$ og $Φ$ er to tilstander i det abstrakte rommet til tilstander i et kvantemekanisk system, og $a$ og $b$ er to komplekse tall, så er $a Ψ + b Φ også$ en gyldig tilstand. (Enten den nullvektor regnes som en gyldig tilstand ( "no-system Foreliggende") er et spørsmål om definisjon. Den nullvektor blir ikke iallfall beskriver en vakuumtilstand i kvantefeltteori.) Settet av tillatte tilstander er et vektorrom .

Denne likheten er selvsagt ikke tilfeldig. Det er også et skille mellom mellomrommene å huske på.

Representasjoner

Grunnleggende tilstander er preget av et sett med kvantetall. Dette er et sett med egenverdier for et maksimalt sett med pendlende observasjoner . Fysiske observerbare er representert av lineære operatører, også kalt observerbare, på vektorrommet. Maksimalitet betyr at det ikke kan legges til settet ytterligere algebraisk uavhengige observasjoner som pendler med de som allerede er tilstede. Et valg av et slikt sett kan kalles et valg av representasjon .

Det er et postulat av kvantemekanikk at en fysisk observerbar mengde av et system, for eksempel posisjon, momentum eller spinn, er representert av en lineær hermitisk operatør på statsrommet . De mulige resultatene for måling av mengden er operatørens egenverdier . På et dypere nivå oppstår de fleste observerbare, kanskje alle, som generatorer av symmetrier .
Den fysiske tolkningen er at et slikt sett representerer det som - i teorien - samtidig kan måles med vilkårlig presisjon. Den Heisenberg usikkerhet knyttet forbyr samtidige nøyaktige målinger av to ikke-pendling observables.
Settet er ikke-unikt. Det kan for eksempel for et ettpartikkelsystem være posisjon og spinn $z$ -projeksjon, $(x, S z)$ , eller det kan være momentum og spinn $y$ -projeksjon, $(p, S y)$ . I dette tilfellet pendler ikke operatøren som tilsvarer posisjonen (en multiplikasjonsoperator i posisjonsrepresentasjonen) og operatøren som tilsvarer momentum (en differensialoperatør i posisjonsrepresentasjonen).
Når en representasjon er valgt, er det fortsatt vilkårlighet. Det gjenstår å velge et koordinatsystem. Dette kan for eksempel svare til et valg av $x, y$ - og $z$ -akse, eller et valg av krumme lineære koordinater som eksemplifisert av de sfæriske koordinatene som brukes for hydrogenbølge -bølgefunksjonene. Dette siste valget fikser også et grunnlag i det abstrakte Hilbert -rommet. Grunntilstandene er merket med kvantetallene som tilsvarer det maksimale settet med pendlende observasjoner og et passende koordinatsystem.

De abstrakte tilstandene er "abstrakte" bare ved at et vilkårlig valg som er nødvendig for en bestemt eksplisitt beskrivelse av det, ikke er gitt. Dette er det samme som å si at det ikke er gitt noe valg av maksimalt sett med pendlende observasjoner. Dette er analogt med et vektorrom uten et spesifisert grunnlag. Bølgefunksjoner som tilsvarer en tilstand er følgelig ikke unike. Denne ikke-særegenheten gjenspeiler den ikke-særegenheten i valget av et maksimalt sett med pendlende observasjoner. For en spinnpartikkel i én dimensjon, til en bestemt tilstand tilsvarer det to bølgefunksjoner, $Ψ (x, S z)$ og $Ψ (p, S y)$ , som begge beskriver den samme tilstanden.

For hvert valg av maksimale pendlingssett med observerbare elementer for det abstrakte tilstandsrommet, er det en tilsvarende representasjon som er knyttet til et funksjonsrom for bølgefunksjoner.
Mellom alle disse forskjellige funksjonsrommene og det abstrakte tilstandsrommet er det en-til-en-korrespondanser (her ser man bort fra normalisering og ikke-observerbare fasefaktorer), og fellesnevner her er en spesiell abstrakt tilstand. Forholdet mellom momentum og posisjon rombølgefunksjoner, for eksempel som beskriver den samme tilstanden, er Fourier -transformasjonen .

Hvert valg av representasjon bør tenkes som å spesifisere et unikt funksjonsrom der bølgefunksjoner som tilsvarer det valg av representasjon lever. Denne distinksjonen beholdes best, selv om man kan argumentere for at to slike funksjonsrom er matematisk like, f.eks. Settet med firkantede integrerbare funksjoner. Man kan da tenke på funksjonsrommene som to forskjellige kopier av det settet.

Indre produkt

Det er en ekstra algebraisk struktur på vektorrommene i bølgefunksjoner og det abstrakte tilstandsrommet.

Fysisk tolkes forskjellige bølgefunksjoner for å overlappe til en viss grad. Et system i en tilstand $Ψ$ som ikke overlapper med en tilstand $Φ$ kan ikke bli funnet å være i tilstanden $Φ$ ved måling. Men hvis $Φ 1, Φ 2, ...$ overlapper $Ψ$ til en viss grad, er det en sjanse for at måling av et system beskrevet av $Ψ$ vil bli funnet i tilstandene $Φ 1, Φ 2,\dots$ . Også valgregler observeres gjelder. Disse er vanligvis formulert for å bevare noen kvantetall. Dette betyr at visse prosesser som er tillatt fra noen perspektiver (f.eks. Bevaring av energi og momentum) ikke skjer fordi de første og siste totale bølgefunksjonene ikke overlapper hverandre.
Matematisk viser det seg at løsninger på Schrödinger -ligningen for bestemte potensialer er ortogonale på en eller annen måte, dette er vanligvis beskrevet av en integrert

{\ displaystyle \ int \ Psi _ {m}^{*} \ Psi _ {n} w \, dV = \ delta _ {nm},}

hvor

m, n

er (sett av) indekser (kvantetall) merking forskjellige løsninger, det strengt positiv funksjon

w

kalles en vektfunksjon, og

δ mn

er Kronecker delta . Integrasjonen tar over hele det relevante rommet.

Dette motiverer introduksjonen av et indre produkt på vektorrommet i abstrakte kvantetilstander, kompatibelt med de matematiske observasjonene ovenfor når de går over til en representasjon. Det er betegnet $(Ψ, Φ)$ , eller i Bra $-ket$ -notasjonen $⟨Ψ | Φ⟩$ . Det gir et komplekst tall. Med det indre produktet er funksjonsrommet et indre produktrom . Det eksplisitte utseendet til det indre produktet (vanligvis en integral eller en sum av integraler) avhenger av valg av representasjon, men det komplekse tallet $(Ψ, Φ)$ gjør det ikke. Mye av den fysiske tolkningen av kvantemekanikk stammer fra Born -regelen . Den sier at sannsynligheten $p$ for å finne tilstanden $Φ$ gitt systemet er i tilstanden $Ψ$ er ved måling

{\ displaystyle p = | (\ Phi, \ Psi) |^{2},}

hvor $Φ$ og $Ψ$ antas normalisert. Vurder et spredningseksperiment . I kvantefeltteorien, hvis $Φ ut$ beskriver en tilstand i "fjern fremtid" (en "ut tilstand") etter at interaksjoner mellom spredende partikler har opphørt, og $Ψ i$ en "i tilstand" i "fjern fortid", så er mengdene $(Φ ut, Ψ inn)$ , med $Φ ut$ og $Ψ i$ varierende over et komplett sett med henholdsvis i tilstander og ut tilstander, kalles S-matrisen eller spredningsmatrisen . Kunnskap om det er faktisk å ha løst teorien for hånden, i hvert fall så langt som spådommene går. Målbare mengder som forfallshastigheter og spredningstverrsnitt er beregningsbare fra S-matrisen.

Hilbert plass

Observasjonene ovenfor innkapsler essensen av funksjonsrommene som bølgefunksjonene er elementer av. Beskrivelsen er imidlertid ikke fullstendig ennå. Det er et ytterligere teknisk krav til funksjonsrommet, det for fullstendighet , som gjør at man kan ta grenser for sekvenser i funksjonsrommet, og sikre at hvis grensen eksisterer, er det et element i funksjonsrommet. Et komplett indre produktrom kalles et Hilbert -rom . Egenskapen til fullstendighet er avgjørende for avanserte behandlinger og anvendelser av kvantemekanikk. For eksempel er eksistensen av projeksjonsoperatører eller ortogonale projeksjoner avhengig av plassens fullstendighet. Disse projiseringsoperatørene er i sin tur avgjørende for utsagnet og beviset på mange nyttige setninger, f.eks. Spektralsetningen . Det er ikke veldig viktig i innledende kvantemekanikk, og tekniske detaljer og lenker kan bli funnet i fotnoter som den som følger. Plassen $L 2$ er et Hilbert -rom, med indre produkt presentert senere. Funksjonsrommet i eksempelet på figuren er et underrom av $L 2$ . Et underrom til et Hilbert -rom er et Hilbert -rom hvis det er lukket.

Oppsummert utgjør settet med alle mulige normaliserbare bølgefunksjoner for et system med et bestemt valg av grunnlag, sammen med nullvektoren, et Hilbert -rom.

Ikke alle funksjoner av interesse er elementer i noe Hilbert -rom, sier $L 2$ . Det mest tydelige eksemplet er settet med funksjoner $e 2 πi p \cdot x ⁄ h$ . Dette er planbølgeløsninger av Schrödinger -ligningen for en fri partikkel, men er ikke normaliserbare, derfor ikke i $L 2$ . Men de er likevel grunnleggende for beskrivelsen. Man kan ved å bruke dem uttrykke funksjoner som er normaliserbare ved hjelp av bølgepakker . De er på en måte et grunnlag (men ikke et Hilbert -romgrunnlag eller et Hamel -grunnlag ) der bølgefunksjoner av interesse kan uttrykkes. Det er også artefakten "normalisering til en delta -funksjon" som ofte brukes for notasjonell bekvemmelighet, se lenger ned. Delta -funksjonene i seg selv er heller ikke firkantet integrerbare.

Beskrivelsen ovenfor av funksjonsrommet som inneholder bølgefunksjonene er for det meste matematisk motivert. Funksjonsrommene er på grunn av fullstendighet veldig store i en viss forstand. Ikke alle funksjoner er realistiske beskrivelser av noe fysisk system. For eksempel kan man i funksjonsrommet $L 2$ finne funksjonen som tar verdien $0$ for alle rasjonelle tall og $- i$ for irrationalene i intervallet $[0, 1]$ . Dette er firkantet integrerbart, men kan neppe representere en fysisk tilstand.

Vanlige Hilbert -rom

Mens løsningsrommet som helhet er et Hilbert -rom, er det mange andre Hilbert -rom som vanligvis forekommer som ingredienser.

Firkantet integrerbart kompleks verdsatt funksjoner på intervallet $[0, 2 π]$ . Settet ${e int /2 π, n \in ℤ}$ er et Hilbert $-romgrunnlag$ , dvs. et maksimalt ortonormalt sett.
Den Fourier-transformasjonen tar funksjoner i det ovennevnte plass til elementer av den $l 2 (ℤ)$ , stedet for firkant summable funksjoner $ℤ \to ℂ$ . Det siste rommet er et Hilbert -rom, og Fourier -transformasjonen er en isomorfisme av Hilbert -rom. Grunnlaget er ${e i, i \in ℤ}$ med $e i (j) = δ ij, i, j \in ℤ$ .
Det mest grunnleggende eksemplet på spenning av polynomer er i plassen med firkantede integrerbare funksjoner på intervallet $[-1, 1]$ som Legendre -polynomene er et Hilbert -romgrunnlag (komplett ortonormalt sett).
De firkantede integrerbare funksjonene på enhetssfæren $S 2$ er et Hilbert -rom. Basisfunksjonene i dette tilfellet er de sfæriske harmoniske . Legendre -polynomene er ingredienser i de sfæriske harmonikkene. De fleste problemer med rotasjonssymmetri vil ha "den samme" (kjente) løsningen med hensyn til den symmetrien, så det opprinnelige problemet reduseres til et problem med lavere dimensjonalitet.
De tilhørende Laguerre -polynomene vises i problemet med hydrogenbølgefunksjonen etter å ha tatt ut de sfæriske harmonikkene. Disse spenner over Hilbert-rommet med firkantede integrerbare funksjoner på det semi-uendelige intervallet $[0, \infty)$ .

Mer generelt kan man vurdere en enhetlig behandling av alle andre ordens polynomløsninger til Sturm - Liouville -ligningene i setting av Hilbert -rom. Disse inkluderer polynomene Legendre og Laguerre så vel som Chebyshev -polynomene , Jacobi -polynomene og eremittpolynomene . Alle disse dukker faktisk opp i fysiske problemer, de sistnevnte i den harmoniske oscillatoren , og det som ellers er en forvirrende labyrint av egenskaper til spesielle funksjoner, blir til en organisert mengde fakta. For dette, se Byron & Fuller (1992 , kapittel 5).

Det forekommer også endelige dimensjonale Hilbert-mellomrom. Plassen $ℂ n$ er et Hilbert $-rom$ med dimensjon $n$ . Det indre produktet er standard indre produkt på disse mellomrommene. I den ligger "spinndelen" av en enkelt partikkelbølgefunksjon.

I den ikke-relativistiske beskrivelsen av et elektron har man $n = 2$ og den totale bølgefunksjonen er en løsning av Pauli-ligningen .
I den tilsvarende relativistiske behandlingen løser $n = 4$ og bølgefunksjonen Dirac -ligningen .

Med flere partikler er situasjonene mer kompliserte. Man må benytte tensorprodukter og bruke representasjonsteori for de involverte symmetri -gruppene (henholdsvis rotasjonsgruppen og Lorentz -gruppen ) for å trekke ut tensorproduktet mellomrommene der (total) spinnbølgefunksjonene ligger. (Ytterligere problemer oppstår i det relativistiske tilfellet med mindre partiklene er frie. Se Bethe -Salpeter -ligningen .) Tilsvarende bemerkninger gjelder begrepet isospin , som symmetri -gruppen er SU (2) . Modellene av atomkreftene på sekstitallet (fremdeles nyttige i dag, se atomkraft ) brukte symmetri -gruppen SU (3) . Også i dette tilfellet ligger delen av bølgefunksjonene som tilsvarer de indre symmetriene i noen $ℂ n$ eller underrom av tensorprodukter i slike mellomrom.

I kvantefeltteorien er det underliggende Hilbert -rommet Fock -rom . Den er bygget fra frie enkeltpartikkeltilstander, det vil si bølgefunksjoner når en representasjon er valgt, og kan romme ethvert begrenset, ikke nødvendigvis konstant i tid, antall partikler. Den interessante (eller rettere sagt traktable ) dynamikken ligger ikke i bølgefunksjonene, men i feltoperatørene som er operatører som virker på Fock -plass. Dermed er Heisenberg -bildet det vanligste valget (konstante tilstander, tidsvarierende operatører).

På grunn av systemets uendelige dimensjonale natur, er de passende matematiske verktøyene studieobjekter i funksjonell analyse .

Forenklet beskrivelse

Kontinuiteten til bølgefunksjonen og dens første romlige derivat (i x -retningen, y- og z -koordinatene ikke vist), på et tidspunkt t .

Ikke alle innledende lærebøker tar den lange veien og introduserer det fulle Hilbert-romaskineriet, men fokuset er på den ikke-relativistiske Schrödinger-ligningen i posisjonsrepresentasjon for visse standardpotensialer. Følgende begrensninger på bølgefunksjonen er noen ganger eksplisitt formulert for at beregningene og fysisk tolkning skal være fornuftig:

Bølgefunksjonen må være kvadratisk integrerbar . Dette er motivert av København -tolkningen av bølgefunksjonen som en sannsynlighetsamplitude.
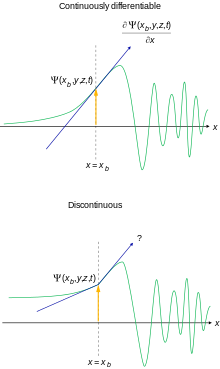
Den må være overalt kontinuerlig og overalt kontinuerlig differensierbar . Dette er motivert av fremkomsten av Schrödinger -ligningen for de fleste fysisk rimelige potensialene.

Det er mulig å slappe av disse forholdene noe for spesielle formål. Hvis disse kravene ikke er oppfylt, er det ikke mulig å tolke bølgefunksjonen som en sannsynlighetsamplitude.

Dette endrer ikke strukturen til Hilbert-rommet som disse bestemte bølgefunksjonene bor i, men underrommet til de kvadratintegrerbare funksjonene $L 2$ , som er et Hilbert-rom, som tilfredsstiller det andre kravet, er ikke lukket i $L 2$ , derfor ikke en Hilbert plass i seg selv. Funksjonene som ikke oppfyller kravene er fortsatt nødvendige av både tekniske og praktiske årsaker.

Mer om bølgefunksjoner og abstrakt tilstandsrom

Som det er demonstrert, utgjør settet av alle mulige bølgefunksjoner i noen representasjoner for et system et generelt uendelig dimensjonalt Hilbert-rom. På grunn av flere mulige valg av representasjonsgrunnlag, er disse Hilbert -mellomrom ikke unike. Man snakker derfor om et abstrakt Hilbert -rom, statsrom , der valg av representasjon og grunnlag er ubestemt. Nærmere bestemt er hver tilstand representert som en abstrakt vektor i statlig rom. En kvantetilstand $| Ψ⟩$ i en hvilken som helst representasjon uttrykkes generelt som en vektor

{\ displaystyle | \ Psi \ rangle = \ sum _ {\ boldsymbol {\ alpha}} \ int d^{m} \! {\ boldsymbol {\ omega}} \, \, \ Psi ({\ boldsymbol {\ alpha }}, {\ boldsymbol {\ omega}}, t) \, | {\ boldsymbol {\ alpha}}, {\ boldsymbol {\ omega}} \ rangle}

hvor

$| α, co ⟩$ basisvektorene til den valgte representasjon
$d m ω = dω 1 dω 2 ... dω m$ et " differensialvolumelement " i de kontinuerlige frihetsgrader
$Ψ (α, ω, t)$ en komponent av vektoren $| Ψ⟩$ , kalt bølgefunksjon av systemet
$α = (α 1, α 2, ..., α n)$ dimensjonsløse diskrete kvantetall
$ω = (ω 1, ω 2, ..., ω m)$ kontinuerlige variabler (ikke nødvendigvis dimensjonsløse)

Disse kvantetallene indekserer komponentene i tilstandsvektoren. Alle $α$ er mer i et $n$ -dimensjonalt sett $A = A 1 \times A 2 \times ... A n$ hvor hvert $A i$ er settet med tillatte verdier for $α i$ ; alle $ω$ er i et $m$ -dimensjonalt "volum" $Ω \subseteq ℝ m$ hvor $Ω = Ω 1 \times Ω 2 \times ... Ω m$ og hver $Ω i \subseteq ℝ$ er settet med tillatte verdier for $ω i$ , et delsett av den virkelige tall $ℝ$ . For generalitet er $n$ og $m$ ikke nødvendigvis like.

Eksempel:

(a) For en enkelt partikkel i 3d med spinn s , forsømmelse av andre frihetsgrader, ved bruk av kartesiske koordinater, kan vi ta $α = (s z)$ for partikkelenes spinnkvantum langs z -retningen, og $ω = (x, y, z)$ for partikkelens posisjonskoordinater. Her er $A = { - s, - s + 1, ..., s - 1, s}$ settet med tillatte spinnkvantetall og $Ω = ℝ 3$ er settet av alle mulige partikkelposisjoner i hele 3d posisjonsrom.

(b) Et alternativt valg er $α = (s y)$ for spinnkvantetallet langs y -retningen og $ω = (p x, p y, p z)$ for partikkelens momentumkomponenter. I dette tilfellet er $A$ og $Ω$ de samme som før.

Den sannsynlighetstettheten for å finne systemet ved at staten $|$ $α$ $,$ $co$ $⟩$ IS ${\ displaystyle t}$

{\ displaystyle \ rho _ {\ alpha, \ omega} (t) = | \ Psi ({\ boldsymbol {\ alpha}}, {\ boldsymbol {\ omega}}, t) |^{2}}

Sannsynligheten for å finne system med $α$ i noen eller alle mulige diskrete-variable konfigurasjoner, $D \subseteq A$ og $ω$ i noen eller alle mulige kontinuerlige variabel-konfigurasjoner, $C \subseteq Ω$ , er summen og integralen over tettheten,

{\ displaystyle P (t) = \ sum _ {{\ boldsymbol {\ alpha}} \ in D} \ int _ {C} \ rho _ {\ alpha, \ omega} (t) \, \, d^{ m} \! {\ boldsymbol {\ omega}}}

Siden summen av alle sannsynligheter må være 1, er normaliseringstilstanden

{\ displaystyle 1 = \ sum _ {{\ boldsymbol {\ alpha}} \ in A} \ int _ {\ Omega} \ rho _ {\ alpha, \ omega} (t) \, \, d^{m} \! {\ boldsymbol {\ omega}}}

må holde til enhver tid under utviklingen av systemet.

Normaliserings tilstanden krever $ρ d m ω$ for å være dimensjonsløst, ved dimensjonsanalyse $Ψ$ må ha de samme enheter som $(ω 1 ω 2 ... ω m) -1/2$ .

Ontologi

Hvorvidt bølgefunksjonen virkelig eksisterer, og hva den representerer, er store spørsmål i tolkningen av kvantemekanikk . Mange kjente fysikere fra en tidligere generasjon undret seg over dette problemet, for eksempel Schrödinger , Einstein og Bohr . Noen går inn for formuleringer eller varianter av tolkningen i København (f.eks. Bohr, Wigner og von Neumann ), mens andre, for eksempel Wheeler eller Jaynes , tar den mer klassiske tilnærmingen og anser bølgefunksjonen som å representere informasjon i observatørens sinn, dvs. et mål av vår kunnskap om virkeligheten. Noen, inkludert Schrödinger, Bohm og Everett og andre, hevdet at bølgefunksjonen må ha en objektiv, fysisk eksistens. Einstein mente at en fullstendig beskrivelse av fysisk virkelighet burde referere direkte til fysisk rom og tid, forskjellig fra bølgefunksjonen, som refererer til et abstrakt matematisk rom.

Se også

Merknader

Sitater

Generelle kilder

Arons, AB; Peppard, MB (1965). "Einsteins forslag til fotonkonseptet: En oversettelse av Annalen der Physik -papiret fra 1905" (PDF) . American Journal of Physics . 33 (5): 367. Bibcode : 1965AmJPh..33..367A . doi : 10.1119/1.1971542 .
Atkins, PW (1974). Quanta: A Handbook of Concepts . ISBN 978-0-19-855494-3.
Bohr, N. (1985). Kalckar, J. (red.). Niels Bohr - Collected Works: Foundations of Quantum Physics I (1926 - 1932) . Bind 6. Amsterdam: Nord -Holland. ISBN 978-044453289-3. |volume=har ekstra tekst ( hjelp )
Born, M. (1926a). "Zur Quantenmechanik der Stoßvorgange". Z. Phys . 37 (12): 863–867. Bibcode : 1926ZPhy ... 37..863B . doi : 10.1007/bf01397477 . S2CID 119896026 .
Born, M. (1926b). "Quantenmechanik der Stoßvorgange". Z. Phys . 38 (11–12): 803–827. Bibcode : 1926ZPhy ... 38..803B . doi : 10.1007/bf01397184 . S2CID 126244962 .
Born, M. (1927). "Fysiske aspekter ved kvantemekanikk" . Natur . 119 (2992): 354–357. Bibcode : 1927Natur.119..354B . doi : 10.1038/119354a0 .
Born, M. (11. desember 1954). "Den statistiske tolkningen av kvantemekanikk" . Nobelforelesning . Nobelstiftelsen . 122 (3172): 675–9. doi : 10.1126/science.122.3172.675 . PMID 17798674 .
de Broglie, L. (1923). "Stråling - Ondes et quanta" [Stråling - bølger og kvanta]. Inneholder Rendus (på fransk). 177 : 507–510, 548, 630. Online kopi (fransk) Online kopi (engelsk)
de Broglie, L. (1960). Ikke-lineær bølgemekanikk: en årsakstolkning . Amsterdam: Elsevier - via Internett -arkiv .
Byron, FW; Fuller, RW (1992) [Først utgitt 1969]. Matematikk i klassisk og kvantefysikk . Dover Books on Physics (revidert red.). Dover Publications . ISBN 978-0-486-67164-2- via Internett -arkiv .
Camilleri, K. (2009). Heisenberg og tolkningen av kvantemekanikk: Fysikeren som filosof . Cambridge UK: Cambridge University Press. ISBN 978-0-521-88484-6.
Conway, JB (1990). Et kurs i funksjonsanalyse . Utdannet tekst i matematikk. Bind 96. Springer Verlag . ISBN 978-0-387-97245-9. |volume=har ekstra tekst ( hjelp )
Dirac, PAM (1939). "En ny notasjon for kvantemekanikk". Matematiske prosesser fra Cambridge Philosophical Society . 35 (3): 416–418. Bibcode : 1939PCPS ... 35..416D . doi : 10.1017/S0305004100021162 .
Dirac, PAM (1982). Prinsippene for kvantemekanikk . Den internasjonale serien om monografier om fysikk (4. utg.). Oxford University Press. ISBN 0-19-852011-5.
Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" . Annalen der Physik (på tysk). 17 (6): 132–148. Bibcode : 1905AnP ... 322..132E . doi : 10.1002/andp.19053220607 .
Einstein, A. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft Zürich . 18 : 47–62.
Einstein, A. (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift (på tysk). 18 : 121–128. Bibcode : 1917PhyZ ... 18..121E .
Einstein, A. (1998). Schlipp, PA (red.). Albert Einstein: filosof-forsker . Biblioteket for levende filosofer. VII (3. utg.). La Salle Publishing Company, Illinois: Open Court. ISBN 978-0-87548-133-3.
Eisberg, R .; Resnick, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2. utg.). John Wiley & Sons. ISBN 978-0-471-87373-0- via Internett -arkiv .
Greiner, W .; Reinhardt, J. (2008). Quantum Electrodynamics (4. utg.). springer. ISBN 978-354087560-4.
Griffiths, DJ (2004). Introduksjon til kvantemekanikk (2. utg.). Essex England: Pearson Education. ISBN 978-013111892-8.
Griffiths, David (2008). Introduksjon til elementære partikler . Wiley-VCH. s. 162ff. ISBN 978-3-527-40601-2.
ter Haar, D. (1967). Den gamle kvanteteorien . Pergamon Press . s. 167–183 . LCCN 66029628 - via Internett -arkiv .
Hanle, PA (1977), "Erwin Schrodinger's Reaction to Louis de Broglie's Thesis on the Quantum Theory", Isis , 68 (4): 606–609, doi : 10.1086/351880 , S2CID 121913205
Heisenberg, W. (1958). Fysikk og filosofi: revolusjonen i moderne vitenskap . New York: Harper & Row - via Internett -arkiv .
Jaynes, ET (2003). Larry, G. (red.). Sannsynlighetsteori: Vitenskapens logikk . Cambridge University Press . ISBN 978-0-521 59271-0.
Landau, LD ; Lifshitz, EM (1977). Kvantemekanikk: Ikke-relativistisk teori . Vol. 3 (3. utg.). Pergamon Press . ISBN 978-0-08-020940-1. |volume=har ekstra tekst ( hjelp ) Online kopi
Lerner, RG ; Trigg, GL (1991). Encyclopaedia of Physics (2. utg.). VHC forlag. ISBN 978-0-89573-752-6- via Internett -arkiv .
Ludwig, G. (1968). Bølgemekanikk . Oxford UK: Pergamon Press. ISBN 978-0-08-203204-5. LCCN 66-30631 -via Internett-arkiv .
Martin, BR; Shaw, G. (2008). Partikkelfysikk . Manchester Physics Series (3. utg.). John Wiley & Sons. ISBN 978-0-470-03294-7.
Murdoch, D. (1987). Niels Bohrs fysikkfilosofi . Cambridge UK: Cambridge University Press. ISBN 978-0-521-33320-7- via Internett -arkiv .
Newton, RG (2002). Quantum Physics: en tekst for kandidatstudenter . New York: Springer. ISBN 978-0-387-95473-8.
Pauli, Wolfgang (1927). "Zur Quantenmechanik des magnetischen Elektrons". Zeitschrift für Physik (på tysk). 43 (9–10): 601–623. Bibcode : 1927ZPhy ... 43..601P . doi : 10.1007/bf01397326 . S2CID 128228729 .
Peleg, Y .; Pnini, R .; Zaarur, E .; Hecht, E. (2010). Kvantemekanikk . Schaums konturer (2. utg.). McGraw Hill. ISBN 978-0-07-162358-2.
Rae, AIM (2008). Kvantemekanikk . Bind 2 (5. utg.). Taylor & Francis Group. ISBN 978-1-5848-89700. |volume=har ekstra tekst ( hjelp )
Schrödinger, E. (1926). "En undulatory theory of the Mechanics of Atoms and Molecules" (PDF) . Fysisk gjennomgang . 28 (6): 1049–1070. Bibcode : 1926PhRv ... 28.1049S . doi : 10.1103/PhysRev.28.1049 . Arkivert fra originalen (PDF) 17. desember 2008.
Shankar, R. (1994). Principles of Quantum Mechanics (2. utg.). ISBN 978-030644790-7.
Tipler, PA; Mosca, G .; Freeman (2008). Fysikk for forskere og ingeniører - med moderne fysikk (6. utg.). ISBN 978-0-7167-8964-2.
Weinberg, S. (2002), The Quantum Theory of Fields , 1 , Cambridge University Press, ISBN 978-0-521-55001-7- via Internett -arkiv
Weinberg, S. (2013), Forelesninger i kvantemekanikk , Cambridge University Press, ISBN 978-1-107-02872-2
Wheeler, JA ; Zurek, WH (1983). Kvanteteori og måling . Princeton NJ: Princeton University Press.
Young, HD; Freedman, RA (2008). Pearson (red.). Sears 'og Zemanskys universitetsfysikk (12. utg.). Addison-Wesley. ISBN 978-0-321-50130-1.
Zettili, N. (2009). Quantum Mechanics: Concepts and Applications (2. utg.). ISBN 978-0-470-02679-3.
Zwiebach, Barton (2009). Et første kurs i strengteori . Cambridge University Press. ISBN 978-0-521-88032-9.

Videre lesning

Kim, Yong-Ki (2. september 2000). Praktisk atomfysikk (PDF) . Nasjonalt institutt for standarder og teknologi. s. 1 (55 s). Arkivert fra originalen (PDF) 22. juli 2011.
Polkinghorne, John (2002). Kvanteteori, en veldig kort introduksjon . Oxford University Press. ISBN 978-0-19-280252-1.

Languages

In other projects