Jacobi elliptiske funksjoner - Jacobi elliptic functions

I matematikk er Jacobi elliptiske funksjoner et sett med grunnleggende elliptiske funksjoner , og hjelpeteta -funksjoner , som er av historisk betydning. De finnes i beskrivelsen av bevegelsen til en pendel (se også pendel (matematikk) ), så vel som i utformingen av elektroniske elliptiske filtre . Mens trigonometriske funksjoner er definert med referanse til en sirkel, er Jacobi elliptiske funksjoner en generalisering som refererer til andre kjeglesnitt , ellipsen spesielt. Forholdet til trigonometriske funksjoner er inneholdt i notasjonen, for eksempel ved den matchende notasjonen${\ displaystyle \ operatorname {sn}}$for . Jacobi elliptiske funksjoner brukes oftere i praktiske problemer enn Weierstrass elliptiske funksjoner, ettersom de ikke krever at begreper om kompleks analyse defineres og/eller forstås. De ble introdusert av Carl Gustav Jakob Jacobi  ( 1829 ). ${\ displaystyle \ sin}$

Oversikt

Det grunnleggende rektangelet i det komplekse planet av ${\ displaystyle u}$

Det er tolv Jacobi elliptiske funksjoner merket med der og er noen av bokstavene , , , og . (Skjemaets funksjoner er trivielt satt til enhet for notasjonell fullstendighet.) Er argumentet, og er parameteren, som begge kan være komplekse. ${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ operatorname {pp} (u, m)}$${\ displaystyle u}$${\ displaystyle m}$

I argumentets komplekse plan danner de tolv funksjonene et gjentagende gitter av enkle poler og nuller . Avhengig av funksjonen vil ett repeterende parallellogram, eller enhetscelle, ha lengdesider eller på den virkelige aksen, og eller på den imaginære aksen, hvor og er kjent som kvartalene med den elliptiske integralen av den første typen. Enhetscellens beskaffenhet kan bestemmes ved å inspisere det "ekstra rektangelet" (vanligvis et parallellogram), som er et rektangel dannet av opprinnelsen i det ene hjørnet, og som det diagonalt motsatte hjørnet. Som i diagrammet, er de fire hjørnene av hjelpe rektangel heter , , , og , går mot klokken fra opprinnelsen. Funksjonen vil ha en null i hjørnet og en pol på hjørnet. De tolv funksjonene tilsvarer de tolv måtene å arrangere disse polene og nullene i hjørnene av rektanglet. ${\ displaystyle u}$${\ displaystyle 2K}$${\ displaystyle 4K}$${\ displaystyle 2K '}$${\ displaystyle 4K '}$${\ displaystyle K = K (m)}$${\ displaystyle K '= K (1-m)}$${\ displaystyle K (\ cdot)}$${\ displaystyle (0,0)}$${\ displaystyle (K, K ')}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$

Når argumentet og parameteren er ekte, med , og vil være ekte og tilleggsparallellogrammet faktisk vil være et rektangel, og Jacobi elliptiske funksjoner vil alle bli reelle verdsatt på den virkelige linjen. ${\ displaystyle u}$${\ displaystyle m}$${\ displaystyle 0 <m <1}$${\ displaystyle K}$${\ displaystyle K '}$

Matematisk er jakobiske elliptiske funksjoner dobbelt periodiske meromorfe funksjoner på det komplekse planet . Siden de er dobbelt periodiske, faktoriserer de gjennom en torus - i realiteten kan domenet deres anses å være en torus, akkurat som cosinus og sinus er i virkeligheten definert på en sirkel. I stedet for å ha bare en sirkel, har vi nå produktet av to sirkler, en ekte og den andre imaginær. Det komplekse planet kan erstattes av en kompleks torus . Omkretsen til den første sirkelen er og den andre , hvor og er kvartalene . Hver funksjon har to nuller og to poler i motsatte posisjoner på torus. Blant punktene , , , det er en null og en pol. ${\ displaystyle 4K}$${\ displaystyle 4K '}$${\ displaystyle K}$${\ displaystyle K '}$${\ displaystyle 0}$${\ displaystyle K}$${\ displaystyle K+iK '}$${\ displaystyle iK '}$

De jakobiske elliptiske funksjonene er da de unike dobbelt periodiske, meromorfe funksjonene som tilfredsstiller følgende tre egenskaper:

• Det er en enkel null i hjørnet , og en enkel stang i hjørnet  .${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$
• Trinnet fra til er lik halve funksjonstiden ; det vil si at funksjonen er periodisk i retningen , med perioden to ganger avstanden fra til . Funksjonen er også periodisk i de to andre retningene, med en periode slik at avstanden fra til et av de andre hjørnene er en kvart periode.${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ operatorname {pq}}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ mathrm {p}}$
• Hvis funksjonen utvides når det gjelder ett av hjørnene, har ledende ledd i utvidelsen en koeffisient på  . Med andre ord, den ledende periode på utvidelsen av ved hjørnet er ; den ledende termen for utvidelsen på hjørnet er , og den ledende termen for en utvidelse i de to andre hjørnene er  .${\ displaystyle \ operatorname {pq} u}$${\ displaystyle u}$${\ displaystyle 1}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ mathrm {p}}$${\ displaystyle u}$${\ displaystyle \ mathrm {q}}$${\ displaystyle u^{-1}}$${\ displaystyle 1}$

Jacobi elliptisk funksjon ${\ displaystyle \ operatorname {sn}}$

Jacobi elliptisk funksjon ${\ displaystyle \ operatorname {cn}}$

Jacobi elliptisk funksjon ${\ displaystyle \ operatorname {dn}}$

Jacobi elliptisk funksjon ${\ displaystyle \ operatorname {sc}}$

Plots med fire Jacobi Elliptic Functions i det komplekse planet av , som illustrerer deres doble periodiske oppførsel. Bilder generert ved hjelp av en versjon av domenefargemetoden . Alle har verdier for parameteren lik .${\ displaystyle u}$${\ displaystyle k}$${\ displaystyle 0.8}$

Notasjon

De elliptiske funksjonene kan gis i en rekke notasjoner, noe som kan gjøre motivet unødvendig forvirrende. Elliptiske funksjoner er funksjoner av to variabler. Den første variabelen kan gis i form av amplituden , eller mer vanlig, i form av gitt nedenfor. Den andre variabelen kan gis i form av parameteren , eller som elliptisk modul , hvor , eller når det gjelder modulvinkelen , hvor . Komplementene til og er definert som og . Disse fire begrepene brukes nedenfor uten kommentarer for å forenkle ulike uttrykk. ${\ displaystyle \ varphi}$${\ displaystyle u}$ ${\ displaystyle m}$ ${\ displaystyle k}$${\ displaystyle k^{2} = m}$ ${\ displaystyle \ alpha}$${\ displaystyle m = \ sin ^{2} \ alpha}$${\ displaystyle k}$${\ displaystyle m}$${\ displaystyle m '= 1-m}$${\ textstyle k '= {\ sqrt {m'}}}$

De tolv Jacobi elliptiske funksjoner er generelt skrevet som der og er noen av bokstavene , , , og . Skjemaets funksjoner er trivielt satt til enhet for notasjonell fullstendighet. De "store" funksjonene antas vanligvis å være , og hvorfra alle andre funksjoner kan utledes og uttrykk ofte skrives utelukkende i form av disse tre funksjonene, men forskjellige symmetrier og generaliseringer uttrykkes ofte mest praktisk ved hjelp av hele settet. (Denne notasjonen skyldes Gudermann og Glaisher og er ikke Jacobis opprinnelige notasjon.) ${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ operatorname {pp} (u, m)}$${\ displaystyle \ operatorname {cn} (u, m)}$${\ displaystyle \ operatorname {sn} (u, m)}$${\ displaystyle \ operatorname {dn} (u, m)}$

Parameteren

Funksjonene er notasjonelt knyttet til hverandre av multiplikasjonsregelen: (argumenter undertrykt)

${\ displaystyle \ operatorname {pq} \ cdot \ operatorname {p'q '} = \ operatorname {pq'} \ cdot \ operatorname {p'q}}$

hvorfra andre ofte brukte relasjoner kan utledes:

${\ displaystyle {\ frac {\ operatorname {pr}} {\ operatorname {qr}}} = \ operatorname {pq}}$

${\ displaystyle \ operatorname {pr} \ cdot \ operatorname {rq} = \ operatorname {pq}}$

${\ displaystyle {\ frac {1} {\ operatorname {qp}}} = \ operatorname {pq}}$

Multiplikasjonsregelen følger umiddelbart av identifiseringen av elliptiske funksjoner med Neville theta -funksjonene

${\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {\ operatorname {p}} (u, m)} {\ theta _ {\ operatorname {q}} (u, m) }}}$

Definisjon som inverser av elliptiske integraler

Modell av amplitude (målt langs vertikal akse) som en funksjon av uavhengige variabler u og k

Definisjonen ovenfor, når det gjelder de unike meromorfe funksjonene som tilfredsstiller visse egenskaper, er ganske abstrakt. Det er en enklere, men helt lik definisjon, som gir elliptiske funksjoner som inverser av den ufullstendige elliptiske integralen av den første typen. La

${\ displaystyle u = \ int _ {0} ^{\ varphi} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1-m \ sin ^{2} \ theta}}} \ ,.}$

Deretter er den elliptiske sinus sn  u (latin: sinus amplitudinis ) gitt av

${\ displaystyle \ operatorname {sn} u = \ sin \ varphi \,}$

og den elliptiske cosinus cn  u (latin: cosinus amplitudinis ) er gitt av

${\ displaystyle \ operatorname {cn} u = \ cos \ varphi}$

og deltaamplituden dn  u (latin: delta amplitudinis )

${\ displaystyle \ operatorname {dn} u = {\ sqrt {1-m \ sin ^{2} \ varphi}} \ ,.}$

Her kalles vinkelen for amplituden . Noen ganger kalles deltaamplituden . I det ovennevnte er verdien en ledig parameter, vanligvis sett på som ekte, og derfor kan de elliptiske funksjonene tenkes å være gitt av to variabler, amplituden og parameteren  . ${\ displaystyle \ varphi}$${\ displaystyle \ operatorname {dn} u = \ Delta (u)}$${\ displaystyle m}$${\ displaystyle 0 \ leq m \ leq 1}$${\ displaystyle \ varphi}$${\ displaystyle m}$

De resterende ni elliptiske funksjonene er enkelt å bygge fra de tre ovennevnte, og er gitt i et avsnitt nedenfor.

Vær oppmerksom på at når , at u da er lik kvartalsperioden . ${\ displaystyle \ varphi = \ pi /2}$ ${\ displaystyle K}$

Definisjon som trigonometri: Jacobi -ellipsen

Plott av Jacobi -ellipsen ( x ² + y ² /b ² = 1, b reell) og de tolv Jacobi -elliptiske funksjonene pq (u, m) for bestemte verdier av vinkel φ og parameter b . Den solide kurven er ellipsen, med m = 1-1/b ² og u = F (φ, m) hvor F (.,.) Er den elliptiske integralen av den første typen. Den stiplede kurven er enhetssirkelen. Tangentlinjer fra sirkelen og ellipse ved x = cd som krysser x-aksen ved dc er vist med lys grå.

${\ displaystyle \ cos \ varphi, \ sin \ varphi}$er definert på enhetssirkelen, med radius r  = 1 og vinkelen på buelengden til enhetssirkelen målt fra den positive x -aksen. På samme måte er Jacobi elliptiske funksjoner definert på enhetens ellipse, med a  = 1. Let ${\ displaystyle \ varphi =}$

${\ displaystyle {\ begin {align} & x^{2}+{\ frac {y^{2}} {b^{2}}} = 1, \ quad b> 1, \\ & m = 1-{\ frac {1} {b^{2}}}, \ quad 0 <m <1, \\ & x = r \ cos \ varphi, \ quad y = r \ sin \ varphi \ end {align}}}$

deretter:

${\ displaystyle r (\ varphi, m) = {\ frac {1} {\ sqrt {1-m \ sin ^{2} \ varphi}}} \ ,.}$

For hver vinkel parameteren ${\ displaystyle \ varphi}$

${\ displaystyle u = u (\ varphi, m) = \ int _ {0}^{\ varphi} r (\ theta, m) \, d \ theta}$

er beregnet. På enhetssirkelen ( ), ville det være en buelengde. Selv om det ikke ser ut til å bære en direkte geometrisk tolkning i det elliptiske tilfellet, viser det seg å være parameteren som går inn i definisjonen av elliptiske funksjoner. La oss faktisk være et punkt på ellipsen, og la være punktet der enhetssirkelen krysser linjen mellom og opprinnelsen . Så de kjente relasjonene fra enhetssirkelen: ${\ displaystyle a = b = 1}$${\ displaystyle u}$${\ displaystyle u}$${\ displaystyle P = (x, y) = (r \ cos \ varphi, r \ sin \ varphi)}$${\ displaystyle P '= (x', y ') = (\ cos \ varphi, \ sin \ varphi)}$${\ displaystyle P}$${\ displaystyle O}$

${\ displaystyle x '= \ cos \ varphi, \ quad y' = \ sin \ varphi}$

les for ellipsen:

${\ displaystyle x '= \ operatorname {cn} (u, m), \ quad y' = \ operatorname {sn} (u, m).}$

Så projeksjonene av skjæringspunktet til linjen med enhetssirkelen på x - og y -aksene er ganske enkelt og . Disse anslagene kan tolkes som 'definisjon som trigonometri'. Kort oppsummert: ${\ displaystyle P '}$${\ displaystyle OP}$${\ displaystyle \ operatorname {cn} (u, m)}$${\ displaystyle \ operatorname {sn} (u, m)}$

${\ displaystyle \ operatorname {cn} (u, m) = {\ frac {x} {r (\ varphi, m)}}, \ quad \ operatorname {sn} (u, m) = {\ frac {y} {r (\ varphi, m)}}, \ quad \ operatorname {dn} (u, m) = {\ frac {1} {r (\ varphi, m)}}.}$

For og verdien av punktet med og parameteren får vi etter å ha satt inn relasjonen: ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle P}$${\ displaystyle u}$${\ displaystyle m}$

${\ displaystyle r (\ varphi, m) = {\ frac {1} {\ operatorname {dn} (u, m)}}}}$

inn: det: ${\ displaystyle x = r (\ varphi, m) \ cos (\ varphi), y = r (\ varphi, m) \ sin (\ varphi)}$

${\ displaystyle x = {\ frac {\ operatorname {cn} (u, m)} {\ operatorname {dn} (u, m)}}, \ quad y = {\ frac {\ operatorname {sn} (u, m)} {\ operatorname {dn} (u, m)}}.}$

Sistnevnte relasjoner for x - og y -koordinatene til punkter på enhetselipse kan betraktes som generalisering av relasjonene for koordinatene til punkter på enhetssirkelen. ${\ displaystyle x = \ cos \ varphi, y = \ sin \ varphi}$

Tabellen nedenfor oppsummerer uttrykkene for alle Jacobi elliptiske funksjoner pq (u, m) i variablene ( x , y , r ) og ( φ , dn) med${\ displaystyle r = {\ sqrt {x^{2}+y^{2}}}}$

Jacobi elliptiske funksjoner pq [u, m] som funksjoner for {x, y, r} og {φ, dn}

		q
		c	s	n	d
s
	c	1	${\ displaystyle x/y = \ barneseng (\ phi)}$	${\ displaystyle x/r = \ cos (\ phi)}$	${\ displaystyle x = \ cos (\ phi)/\ operatorname {dn}}$
	s	${\ displaystyle y/x = \ tan (\ phi)}$	1	${\ displaystyle y/r = \ sin (\ phi)}$	${\ displaystyle y = \ sin (\ phi)/\ operatorname {dn}}$
	n	${\ displaystyle r/x = \ sec (\ phi)}$	${\ displaystyle r/y = \ csc (\ phi)}$	1	${\ displaystyle r = 1/\ operatorname {dn}}$
	d	${\ displaystyle 1/x = \ operatorname {dn} \ sec (\ phi)}$	${\ displaystyle 1/y = \ operatorname {dn} \ csc (\ phi)}$	${\ displaystyle 1/r = \ operatorname {dn}}$	1

Definisjon når det gjelder Jacobi theta -funksjoner

Tilsvarende kan Jacobis elliptiske funksjoner defineres ut fra hans theta -funksjoner . Hvis vi forkorte som , og henholdsvis som (de theta konstanter ) og deretter theta funksjon elliptiske modulus k er . Hvis vi setter , har vi ${\ displaystyle \ vartheta (0; \ tau)}$${\ displaystyle \ vartheta}$${\ displaystyle \ vartheta _ {01} (0; \ tau), \ vartheta _ {10} (0; \ tau), \ vartheta _ {11} (0; \ tau)}$${\ displaystyle \ vartheta _ {01}, \ vartheta _ {10}, \ vartheta _ {11}}$ ${\ displaystyle k = \ left ({\ vartheta _ {10} \ over \ vartheta} \ right)^{2}}$${\ displaystyle u = \ pi \ vartheta ^{2} z}$

${\ displaystyle {\ begin {align} \ operatorname {sn} (u; k) & =-{\ vartheta \ vartheta _ {11} (z; \ tau) \ over \ vartheta _ {10} \ vartheta _ {01 } (z; \ tau)} \\ [7pt] \ operatorname {cn} (u; k) & = {\ vartheta _ {01} \ vartheta _ {10} (z; \ tau) \ over \ vartheta _ { 10} \ vartheta _ {01} (z; \ tau)} \\ [7pt] \ operatorname {dn} (u; k) & = {\ vartheta _ {01} \ vartheta (z; \ tau) \ over \ vartheta \ vartheta _ {01} (z; \ tau)} \ end {justert}}}$

Siden Jacobi -funksjonene er definert i form av elliptisk modul , må vi invertere dette og finne i form av . Vi starter fra , den komplementære modulen . Som en funksjon av det er ${\ displaystyle k (\ tau)}$${\ displaystyle \ tau}$${\ displaystyle k}$${\ displaystyle k '= {\ sqrt {1-k^{2}}}}$${\ displaystyle \ tau}$

${\ displaystyle k '(\ tau) = \ left ({\ vartheta _ {01} \ over \ vartheta} \ right)^{2}.}$

La oss først definere

${\ displaystyle \ ell = {1 \ over 2} {1 -{\ sqrt {k '}} \ over 1+{\ sqrt {k'}}} = {1 \ over 2} {\ vartheta -\ vartheta _ {01} \ over \ vartheta +\ vartheta _ {01}}.}$

Definer deretter nomen som og utvid som en kraftserie i nomen , vi får ${\ displaystyle q = \ exp (\ pi i \ tau)}$${\ displaystyle \ ell}$${\ displaystyle q}$

${\ displaystyle \ ell = {q+q^{9}+q^{25}+\ cdots \ over 1+2q^{4}+2q^{16}+\ cdots}.}$

Reversjon av serier gir nå

${\ displaystyle q = \ ell +2 \ ell ^{5} +15 \ ell ^{9} +150 \ ell ^{13} +1707 \ ell ^{17} +20910 \ ell ^{21} +268616 \ ell ^{25}+\ cdots.}$

Siden vi kan redusere til det tilfellet hvor den imaginære delen av er større enn eller lik , kan vi anta at den absolutte verdien av er mindre enn eller lik ; for verdier denne lille konvergerer serien ovenfor veldig raskt og lar oss enkelt finne den riktige verdien for . ${\ displaystyle \ tau}$${\ displaystyle {\ sqrt {3}}/2}$${\ displaystyle q}$${\ displaystyle \ exp (-\ pi {\ sqrt {3}}/2) \ ca 0,0658}$${\ displaystyle q}$

Definisjon når det gjelder Neville theta -funksjoner

Jacobi elliptiske funksjoner kan veldig enkelt defineres ved hjelp av Neville theta -funksjonene :

${\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {\ operatorname {p}} (u, m)} {\ theta _ {\ operatorname {q}} (u, m) }}}$

Forenklinger av kompliserte produkter av Jacobi elliptiske funksjoner blir ofte enklere ved bruk av disse identitetene.

Jacobi -transformasjoner

Jacobiens imaginære transformasjoner

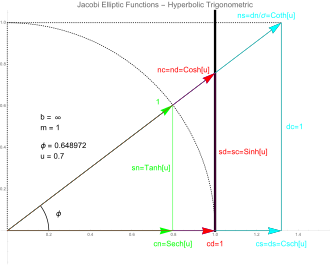
Plott av den degenererte Jacobi -kurven (x ² +y ² /b ² = 1, b = uendelig) og de tolv Jacobi -elliptiske funksjonene pq (u, 1) for en bestemt verdi av vinkel φ. Den solide kurven er den degenererte ellipsen (x ² = 1) med m = 1 og u = F (φ, 1) hvor F (.,.) Er den elliptiske integralen av den første typen .. Den stiplede kurven er enhetssirkelen . Siden dette er Jacobi -funksjonene for m = 0 (sirkulære trigonometriske funksjoner), men med imaginære argumenter, tilsvarer de de seks hyperboliske trigonometriske funksjonene.

Jacobis imaginære transformasjoner relaterer forskjellige funksjoner til den imaginære variabelen iu eller, tilsvarende, relasjoner mellom forskjellige verdier av m -parameteren. Når det gjelder de viktigste funksjonene:

${\ displaystyle \ operatorname {cn} (u, m) = \ operatorname {nc} (i \, u, 1 \!-\! m)}$

${\ displaystyle \ operatorname {sn} (u, m) =-i \ operatorname {sc} (i \, u, 1 \!-\! m)}$

${\ displaystyle \ operatorname {dn} (u, m) = \ operatorname {dc} (i \, u, 1 \!-\! m)}$

Ved å bruke multiplikasjonsregelen kan alle andre funksjoner uttrykkes i form av de tre ovennevnte. Transformasjonene kan generelt skrives som . Tabellen nedenfor viser den angitte pq ( u, m ). (Argumentene er undertrykt) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \!-\! m)}$${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \!-\! m)}$${\ displaystyle (i \, u, 1 \!-\! m)}$

Jacobi Imaginære transformasjoner ${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \!-\! m)}$

		q
		c	s	n	d
s
	c	1	i ns	nc	nd
	s	-er n	1	-jeg	-i sd
	n	cn	jeg cs	1	cd
	d	dn	jeg ds	dc	1

Siden de hyperboliske trigonometriske funksjonene er proporsjonale med de sirkulære trigonometriske funksjonene med imaginære argumenter, følger det at Jacobi -funksjonene vil gi de hyperboliske funksjonene for m = 1. I figuren har Jacobi-kurven degenerert til to vertikale linjer ved x = 1 og x = -1.

De Jacobi -virkelige transformasjonene

De Jacobi -virkelige transformasjonene gir uttrykk for de elliptiske funksjonene i form av alternative verdier på m . Transformasjonene kan vanligvis skrives som . Tabellen nedenfor viser den angitte pq ( u, m ). (Argumentene er undertrykt) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1/m)}$${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1/m)}$${\ displaystyle (k \, u, 1/m)}$

Jacobi Real transformasjoner ${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1/m)}$

		q
		c	s	n	d
s
	c	1	${\ displaystyle k}$ ds	dn	dc
	s	${\ displaystyle {\ frac {1} {k}}}$ sd	1	${\ displaystyle {\ frac {1} {k}}}$ sn	${\ displaystyle {\ frac {1} {k}}}$ sc
	n	nd	${\ displaystyle k}$ ns	1	nc
	d	cd	${\ displaystyle k}$ cs	cn	1

Andre Jacobi -transformasjoner

Jacobis virkelige og imaginære transformasjoner kan kombineres på forskjellige måter for å gi ytterligere tre enkle transformasjoner. De virkelige og imaginære transformasjonene er to transformasjoner i en gruppe ( D ₃ eller anharmonisk gruppe ) på seks transformasjoner. Hvis

${\ displaystyle \ mu _ {R} (m) = 1/m}$

er transformasjonen for m -parameteren i den virkelige transformasjonen, og

${\ displaystyle \ mu _ {I} (m) = 1-m = m '}$

er transformasjonen av m i den imaginære transformasjonen, så kan de andre transformasjonene bygges opp ved påfølgende anvendelse av disse to grunnleggende transformasjonene, og gir bare tre flere muligheter:

${\ displaystyle {\ begynne {justert} \ mu _ {IR} (m) & = & \ mu _ {I} (\ mu _ {R} (m)) & = &-m '/m \\\ mu _ {RI} (m) & = & \ mu _ {R} (\ mu _ {I} (m)) & = & 1/m '\\\ mu _ {RIR} (m) & = & \ mu _ {R} (\ mu _ {I} (\ mu _ {R} (m))) & = &-m/m '\ end {align}}}$

Disse fem transformasjonene, sammen med identitetstransformasjonen (μ _U (m) = m) gir gruppen 6 elementer. Når det gjelder Jacobi elliptiske funksjoner, kan den generelle transformasjonen uttrykkes med bare tre funksjoner:

${\ displaystyle \ operatorname {cs} (u, m) = \ gamma _ {i} \ operatorname {cs '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

${\ displaystyle \ operatorname {ns} (u, m) = \ gamma _ {i} \ operatorname {ns '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

${\ displaystyle \ operatorname {ds} (u, m) = \ gamma _ {i} \ operatorname {ds '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

hvor i = U, I, IR, R, RI eller RIR, som identifiserer transformasjonen, er γ _i en multiplikasjonsfaktor som er felles for disse tre funksjonene, og primen indikerer den transformerte funksjonen. De ni andre transformerte funksjonene kan bygges opp fra de tre ovennevnte. Grunnen til at cs, ns, ds -funksjonene ble valgt for å representere transformasjonen er at de andre funksjonene vil være forhold mellom disse tre (bortsett fra deres inverser) og multiplikasjonsfaktorene vil avbrytes.

Tabellen nedenfor viser multiplikasjonsfaktorene for de tre ps -funksjonene, de transformerte m'ene og de transformerte funksjonsnavnene for hver av de seks transformasjonene. (Som vanlig er k ² = m, 1-k ² = k ₁ ² = m 'og argumentene ( ) undertrykt) ${\ displaystyle \ gamma _ {i} u, \ mu _ {i} (m)}$

Parametere for de seks transformasjonene

Transformasjon i	${\ displaystyle \ gamma _ {i}}$	${\ displaystyle \ mu _ {i} (m)}$	cs '	ns '	ds '
U	1	m	cs	ns	ds
Jeg	Jeg	m '	ns	cs	ds
IR	ik	-m '/m	ds	cs	ns
R	k	1/m	ds	ns	cs
RI	ik 1	1/m '	ns	ds	cs
RIR	k 1	-m/m '	cs	ds	ns

Således kan vi for eksempel bygge følgende tabell for RIR -transformasjonen. Transformasjonen er generelt skrevet (Argumentene undertrykkes) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \, \ operatorname {pq '} (k' \, u, -m/m ')}$${\ displaystyle (k '\, u, -m/m')}$

RIR -transformasjonen ${\ displaystyle \ gamma _ {\ operatorname {pq}} \, \ operatorname {pq '} (k' \, u, -m/m ')}$

		q
		c	s	n	d
s
	c	1	k 'cs	cd	cn
	s	${\ displaystyle {\ frac {1} {k '}}}$ sc	1	${\ displaystyle {\ frac {1} {k '}}}$ sd	${\ displaystyle {\ frac {1} {k '}}}$ sn
	n	dc	${\ displaystyle k '}$ ds	1	dn
	d	nc	${\ displaystyle k '}$ ns	nd	1

Verdien av Jacobi-transformasjonene er at ethvert sett med Jacobi elliptiske funksjoner med alle komplekse verdier parameter m kan konverteres til et annet sett som 0 <= m <= 1 og for virkelige verdier av u vil funksjonsverdiene være reelle .

Jacobi -hyperbola

Plott av Jacobi -hyperbola ( x ² + y ² /b ² = 1, b imaginær) og de tolv Jacobi -elliptiske funksjonene pq (u, m) for bestemte verdier av vinkel φ og parameter b . Den solide kurven er hyperbola, med m = 1-1/b ² og u = F (φ, m) hvor F (.,.) Er den elliptiske integralen av den første typen. Den stiplede kurven er enhetssirkelen. For ds-dc trekanten, σ = sin (φ) cos (φ) .

Vår ellipse introduserer komplekse tall og har en tilhørende hyperbola:

${\ displaystyle x^{2}-{\ frac {y^{2}} {b^{2}}} = 1}$

fra å bruke Jacobis imaginære transformasjon til elliptiske funksjoner i ligningen ovenfor for x og  y .

${\ displaystyle x = {\ frac {1} {\ operatorname {dn} (u, 1-m)}}, \ quad y = {\ frac {\ operatorname {sn} (u, 1-m)} {\ operatornavn {dn} (u, 1-m)}}}$

Det følger at vi kan sette . Så vår ellipse har en dobbel ellipse med m erstattet av 1-m. Dette fører til den komplekse torus som er nevnt i introduksjonen. Vanligvis kan m være et komplekst tall, men når m er reelt og m <0, er kurven en ellipse med hovedakse i x -retningen. Ved m = 0 er kurven en sirkel, og for 0 <m <1 er kurven en ellipse med hovedakse i y -retningen. Ved m = 1 degenererer kurven til to vertikale linjer ved x =+/- 1. For m> 1 er kurven en hyperbola. Når m er kompleks, men ikke reell, er x eller y eller begge komplekse og kurven kan ikke beskrives på et reelt xy -diagram. ${\ displaystyle x = \ operatorname {dn} (u, 1-m), y = \ operatorname {sn} (u, 1-m)}$

Mindre funksjoner

Å reversere rekkefølgen på de to bokstavene i funksjonsnavnet resulterer i gjensidige av de tre funksjonene ovenfor:

${\ displaystyle {\ begin {align} \ operatorname {ns} (u) = {\ frac {1} {\ operatorname {sn} (u)}}, \ qquad \ operatorname {nc} (u) = {\ frac {1} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {nd} (u) = {\ frac {1} {\ operatorname {dn} (u)}}. \ End {align}} }$

På samme måte tilsvarer forholdene mellom de tre hovedfunksjonene den første bokstaven i telleren etterfulgt av den første bokstaven i nevneren:

${\ displaystyle {\ begin {align} \ operatorname {sc} (u) = {\ frac {\ operatorname {sn} (u)} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {sd} (u) = {\ frac {\ operatorname {sn} (u)} {\ operatorname {dn} (u)}}, \ qquad \ operatorname {dc} (u) = {\ frac {\ operatorname {dn} ( u)} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {ds} (u) = {\ frac {\ operatorname {dn} (u)} {\ operatorname {sn} (u)}} , \ qquad \ operatorname {cs} (u) = {\ frac {\ operatorname {cn} (u)} {\ operatorname {sn} (u)}}, \ qquad \ operatorname {cd} (u) = {\ frac {\ operatorname {cn} (u)} {\ operatorname {dn} (u)}}. \ end {align}}}$

Mer kompakt har vi

${\ displaystyle \ operatorname {pq} (u) = {\ frac {\ operatorname {pn} (u)} {\ operatorname {qn} (u)}}}$

hvor p og q er noen av bokstavene s, c, d.

Periodisitet, poler og rester

Plott av fasen for de tolv Jacobi elliptiske funksjonene pq (u, m) som et funksjonskompleks argument u, med poler og nuller angitt. Plottene er over en hel syklus i den virkelige og imaginære retningen med den fargede delen som indikerer fase i henhold til fargehjulet nederst til høyre (som erstatter den trivielle dd -funksjonen). Regioner med amplitude under 1/3 er farget svart, noe som grovt angir plasseringen av et null, mens regioner med amplitude over 3 er farget hvite, grovt angir posisjonen til en pol. Alle plott bruker m = 2/3 med K = K (m), K '= K (1-m), K (.) Er den komplette elliptiske integralen av den første typen. Piler ved polene peker i retning av nullfase. Høyre og venstre pil antyder henholdsvis positive og negative reelle rester. Pil opp og ned antyder henholdsvis positive og negative imaginære rester.

I det komplekse planet til argumentet u danner de Jacobi elliptiske funksjonene et repeterende mønster av poler (og nuller). Restene av polene har alle samme amplitude, og skiller seg bare i tegn. Hver funksjon pq (u, m) har en invers funksjon qp (u, m) der posisjonene til polene og nullene utveksles. Gjentagelsesperiodene er generelt forskjellige i den virkelige og imaginære retningen, derav bruken av begrepet "dobbelt periodisk" for å beskrive dem.

Den doble periodisiteten til Jacobi elliptiske funksjoner kan uttrykkes som:

${\ displaystyle \ operatorname {pq} (u+2 \ alpha K (m)+2i \ beta K (1-m) \ ,, \, m) = (-1)^{\ gamma} \ operatorname {pq} (u, m)}$

hvor α og β er et par heltall. K (.) Er den komplette elliptiske integralen av den første typen, også kjent som kvartalsperioden . Kraften til negativ enhet (γ) er gitt i tabellen nedenfor:

${\ displaystyle \ gamma}$

		q
		c	s	n	d
s
	c	0	β	α+β	α
	s	β	0	α	α+β
	n	α+β	α	0	β
	d	α	α+β	β	0

Når faktoren (-1) ^γ er lik -1, uttrykker ligningen kvasi-periodisitet. Når det er lik enhet, uttrykker det full periodisitet. Det kan for eksempel sees at for oppføringene som bare inneholder α når α er jevn, uttrykkes full periodisitet med ligningen ovenfor, og funksjonen har hele perioder på 4K (m) og 2iK (1-m). På samme måte har funksjoner med oppføringer som bare inneholder β hele perioder på 2K (m) og 4iK (1-m), mens de med α + β har hele perioder på 4K (m) og 4iK (1-m).

I diagrammet til høyre, som plotter en gjentagende enhet for hver funksjon, som angir fase sammen med plasseringen av poler og nuller, kan en rekke regelmessigheter noteres: Inversen av hver funksjon er motsatt diagonalen og har samme størrelse enhetscelle, med poler og nuller utvekslet. Stangen og nullarrangementet i det ekstra rektangelet dannet av (0,0), (K, 0), (0, K ') og (K, K') er i samsvar med beskrivelsen av polen og nullplasseringen beskrevet i introduksjonen ovenfor. Størrelsen på de hvite ovalene som indikerer polene er også et grovt mål på amplituden til resten for den polen. Restene av polene nærmest opprinnelsen i figuren (dvs. i det ekstra rektangelet) er oppført i følgende tabell:

Rester av Jacobi Elliptic Functions

		q
		c	s	n	d
s
	c		1	${\ displaystyle -{\ frac {i} {k}}}$	${\ displaystyle -{\ frac {1} {k}}}$
	s	${\ displaystyle -{\ frac {1} {k '}}}$		${\ displaystyle {\ frac {1} {k}}}$	${\ displaystyle -{\ frac {i} {k \, k '}}}$
	n	${\ displaystyle -{\ frac {1} {k '}}}$	1		${\ displaystyle -{\ frac {i} {k '}}}$
	d	-1	1	${\ displaystyle -i}$

Når det er aktuelt, har poler forskjøvet over med 2K eller forskjøvet til høyre med 2K 'samme verdi, men med omvendte tegn, mens de diagonalt motsatt har samme verdi. Vær oppmerksom på at poler og nuller på venstre og nedre kant regnes som en del av enhetscellen, mens de på øvre og høyre kant ikke er det.

Forholdet mellom kvadratene til funksjonene

Forholdet mellom kvadratene til funksjonene kan stammer fra to grunnleggende forhold (Argumenter ( u , m ) undertrykt):

${\ displaystyle \ operatorname {cn} ^{2}+\ operatorname {sn} ^{2} = 1}$

${\ displaystyle \ operatorname {cn} ^{2}+m '\ operatorname {sn} ^{2} = \ operatorname {dn} ^{2}}$

hvor m + m '  = 1 og m  =  k ² . Multiplisering med hvilken som helst funksjon av skjemaet nq gir mer generelle ligninger:

${\ displaystyle \ operatorname {cq} ^{2}+\ operatorname {sq} ^{2} = \ operatorname {nq} ^{2}}$

${\ displaystyle \ operatorname {cq} ^{2}+m '\ operatorname {sq} ^{2} = \ operatorname {dq} ^{2}}$

Med q = d tilsvarer disse trigonometrisk ligningene for enhetssirkelen ( ) og enhetselipse ( ), med x = cd , y = sd og r = nd . Ved å bruke multiplikasjonsregelen kan andre relasjoner utledes. For eksempel: ${\ displaystyle x^{2}+y^{2} = r^{2}}$${\ displaystyle x^{2}+mi^{2} = 1}$

${\ displaystyle-\ operatorname {dn} ^{2}+m '=-m \ operatorname {cn} ^{2} = m \ operatorname {sn} ^{2} -m}$

${\ displaystyle -m '\ operatorname {nd} ^{2}+m' =-mm '\ operatorname {sd} ^{2} = m \ operatorname {cd} ^{2} -m}$

${\ displaystyle m '\ operatorname {sc} ^{2}+m' = m '\ operatorname {nc} ^{2} = \ operatorname {dc} ^{2} -m}$

${\ displaystyle \ operatorname {cs} ^{2}+m '= \ operatorname {ds} ^{2} = \ operatorname {ns} ^{2} -m}$

Addisjonssetninger

Funksjonene tilfredsstiller de to kvadratiske forholdene

${\ displaystyle \ operatorname {cn} ^{2} (u, k)+\ operatorname {sn} ^{2} (u, k) = 1, \,}$

${\ displaystyle \ operatorname {dn} ^{2} (u, k)+k ^{2} \ operatorname {sn} ^{2} (u, k) = 1. \,}$

Fra dette ser vi at (cn, sn, dn) parametriserer en elliptisk kurve som er skjæringspunktet mellom de to kvadrikkene definert av de to ligningene ovenfor. Vi kan nå definere en gruppelov for punkter på denne kurven ved tilleggsformlene for Jacobi -funksjonene

${\ displaystyle {\ begynne {justert} \ operatorname {cn} (x+y) & = {\ operatorname {cn} (x) \ operatorname {cn} (y)-\ operatorname {sn} (x) \ operatorname { sn} (y) \ operatorname {dn} (x) \ operatorname {dn} (y) \ over {1-k ^{2} \ operatorname {sn} ^{2} (x) \ operatorname {sn} ^{ 2} (y)}}, \\ [8pt] \ operatorname {sn} (x+y) & = {\ operatorname {sn} (x) \ operatorname {cn} (y) \ operatorname {dn} (y) +\ operatorname {sn} (y) \ operatorname {cn} (x) \ operatorname {dn} (x) \ over {1-k ^{2} \ operatorname {sn} ^{2} (x) \ operatorname { sn} ^{2} (y)}}, \\ [8pt] \ operatorname {dn} (x+y) & = {\ operatorname {dn} (x) \ operatorname {dn} (y) -k ^{ 2} \ operatorname {sn} (x) \ operatorname {sn} (y) \ operatorname {cn} (x) \ operatorname {cn} (y) \ over {1-k ^{2} \ operatorname {sn} ^ {2} (x) \ operatorname {sn} ^{2} (y)}}. \ End {align}}}$

Dobbelvinkelformler kan enkelt avledes fra ligningene ovenfor ved å sette x = y . Halvvinkelformler har alle formen:

${\ displaystyle \ operatorname {pq} ({\ tfrac {1} {2}} u, m)^{2} = f _ {\ mathrm {p}}/f _ {\ mathrm {q}}}$

hvor:

${\ displaystyle f _ {\ mathrm {c}} = \ operatorname {cn} (u, m)+\ operatorname {dn} (u, m)}$

${\ displaystyle f _ {\ mathrm {s}} = 1- \ operatorname {cn} (u, m)}$

${\ displaystyle f _ {\ mathrm {n}} = 1+\ operatorname {dn} (u, m)}$

${\ displaystyle f _ {\ mathrm {d}} = (1+ \ operatorname {dn} (u, m))-m (1- \ operatorname {cn} (u, m))}$

Spesielle verdier

Verdier for halvering av K:

${\ displaystyle \ operatorname {sn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ frac {1} {\ sqrt {1+{\ sqrt {1-k ^{2}}}}}}}}$og og${\ displaystyle \ operatorname {cn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ frac {\ sqrt [{4}] {1-k^{2} }} {\ sqrt {1+{\ sqrt {1-k^{2}}}}}}}$${\ displaystyle \ operatorname {dn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ sqrt [{4}] {1-k^{2}}}}$

Verdier for tredjedelen av K:

${\ displaystyle \ operatorname {sn} \ left [{\ frac {1} {3}} K \ left ({\ frac {x^{3}} {{\ sqrt {x^{6} +1}}+ 1}} \ right); {\ frac {x^{3}} {{\ sqrt {x^{6} +1}}+1}} \ right] = {\ frac {{\ sqrt {2 {\ sqrt {x^{4} -x^{2} +1}}-x^{2} +2}}+{\ sqrt {x^{2} +1}}-1} {{\ sqrt {2 {\ sqrt {x^{4} -x^{2} +1}}-x^{2} +2}}+{\ sqrt {x^{2} +1}}+1}}}$

For å få x^3 må du ta tangenten til det dobbelte av arktangenten til modulen.

Også denne ligningen fører til sn-verdien til den tredje av K:

${\ displaystyle k^{2} s^{4} -2k^{2} s^{3}+2s-1 = 0}$

${\ displaystyle s = \ operatorname {sn} \ left [{\ tfrac {1} {3}} K (k); k \ right]}$

Disse ligningene fører til de andre verdiene til Jacobi-funksjonene:

${\ displaystyle \ operatorname {cn} \ left [{\ tfrac {2} {3}} K (k); k \ right] = 1- \ operatorname {sn} \ left [{\ tfrac {1} {3} } K (k); k \ høyre]}$

${\ displaystyle \ operatorname {dn} \ left [{\ tfrac {2} {3}} K (k); k \ right] = 1/\ operatorname {sn} \ left [{\ tfrac {1} {3} } K (k); k \ høyre] -1}$

Verdier for femtedelene av K:

Følgende ligning har følgende løsning:

${\ displaystyle 4k^{2} x^{6}+8k^{2} x^{5} +2 (1-k^{2})^{2} x- (1-k^{2}) ^{2} = 0}$

${\ displaystyle x = {\ frac {1} {2}}-{\ frac {1} {2}} k^{2} \ operatorname {sn} \ venstre [{\ tfrac {2} {5}} K (k); k \ right]^{2} \ operatorname {sn} \ left [{\ tfrac {4} {5}} K (k); k \ right]^{2} = {\ frac {\ operatorname {sn} \ venstre [{\ frac {4} {5}} K (k); k \ høyre]^{2}-\ operatorname {sn} \ venstre [{\ frac {2} {5}} K ( k); k \ right]^{2}} {2 \ operatorname {sn} \ left [{\ frac {2} {5}} K (k); k \ right] \ operatorname {sn} \ left [{ \ frac {4} {5}} K (k); k \ høyre]}}}$

For å få sn-verdiene må du sette løsningen x i følgende uttrykk:

${\ displaystyle {\ sqrt {k^{2} +1}} \ operatorname {sn} \ left [{\ tfrac {2} {5}} K (k); k \ right] = {\ sqrt {2 ( -x^{2} -x+1) (x^{2}+1-x {\ sqrt {x^{2} +1}})}}}}$

${\ displaystyle {\ sqrt {k^{2} +1}} \ operatorname {sn} \ left [{\ tfrac {4} {5}} K (k); k \ right] = {\ sqrt {2 ( -x^{2} -x+1) (x^{2}+1+x {\ sqrt {x^{2} +1}})}}}}$

Utvidelse når det gjelder nomen

La nome være , , og la . Da har funksjonene utvidelser som Lambert -serien${\ displaystyle q = \ exp (-\ pi K '(k)/K (k)) = e^{i \ pi \ tau}}$${\ displaystyle \ operatorname {Im} (\ tau)> 0}$${\ displaystyle m = k^{2}}$${\ displaystyle v = \ pi u/(2K (k))}$

${\ displaystyle \ operatorname {sn} (u; k) = {\ frac {2 \ pi} {kK (k)}} \ sum _ {n = 0}^{\ infty} {\ frac {q^{n +1/2}} {1-q^{2n+1}}} \ sin ((2n+1) v),}$

${\ displaystyle \ operatorname {cn} (u; k) = {\ frac {2 \ pi} {kK (k)}} \ sum _ {n = 0}^{\ infty} {\ frac {q^{n +1/2}} {1+q^{2n+1}}} \ cos ((2n+1) v),}$

${\ displaystyle \ operatorname {dn} (u; k) = {\ frac {\ pi} {2K (k)}}+{\ frac {2 \ pi} {K (k)}} \ sum _ {n = 1}^{\ infty} {\ frac {q^{n}} {1+q^{2n}}} \ cos (2nv)}$

når . ${\ displaystyle q \ exp (2 | \ operatorname {Im} (v) |) <1}$

Jacobi elliptiske funksjoner som løsninger av ikke -lineære vanlige differensialligninger

De derivater av de tre grunnleggende Jacobi elliptiske funksjoner er:

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {sn} (z) = \ operatorname {cn} (z) \ operatorname {dn} (z),}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {cn} (z) =-\ operatorname {sn} (z) \ operatorname {dn} (z),}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {dn} (z) =-k^{2} \ operatorname {sn} (z) \ operatorname {cn} (z).}$

Disse kan brukes til å utlede derivatene til alle andre funksjoner som vist i tabellen nedenfor (argumenter (u, m) undertrykt):

Derivater ${\ displaystyle {\ frac {d} {du}} \ operatorname {pq} (u, m)}$

		q
		c	s	n	d
s
	c	0	-ds ns	-dn sn	-m og sd
	s	dc nc	0	cn dn	cd og
	n	dc sc	-cs ds	0	m cd sd
	d	m 'nc sc	-cs ns	-m cn sn	0

Med tilleggssetningene ovenfor og for en gitt k med 0 <  k  <1 er hovedfunksjonene derfor løsninger på følgende ikke -lineære vanlige differensialligninger :

• ${\ displaystyle \ operatorname {sn} (x)}$løser differensialligningene og${\ displaystyle {\ frac {\ mathrm {d}^{2} y} {\ mathrm {d} x^{2}}}+(1+k^{2}) y-2k^{2} y^ {3} = 0}$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right)^{2} = (1-y^{2}) (1-k^{2 } y^{2})}$
• ${\ displaystyle \ operatorname {cn} (x)}$løser differensialligningene og${\ displaystyle {\ frac {\ mathrm {d}^{2} y} {\ mathrm {d} x^{2}}}+(1-2k^{2}) y+2k^{2} y^ {3} = 0}$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right)^{2} = (1-y^{2}) (1-k^{2 }+k^{2} y^{2})}$
• ${\ displaystyle \ operatorname {dn} (x)}$løser differensialligningene og${\ displaystyle {\ frac {\ mathrm {d}^{2} y} {\ mathrm {d} x^{2}}}-(2-k^{2}) y+2y^{3} = 0 }$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right)^{2} = (y^{2} -1) (1-k^{2 } -y^{2})}$

Tilnærming når det gjelder hyperboliske funksjoner

Jacobi elliptiske funksjoner kan utvides når det gjelder de hyperboliske funksjonene. Når det er nær enhet, slik at og høyere krefter kan neglisjeres, har vi: ${\ displaystyle m}$${\ displaystyle m '^{2}}$${\ displaystyle m '}$

• sn ( u ):
  $${\ displaystyle \ operatorname {sn} (u, m) \ approx \ tanh (u)+{\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ operatorname { sech} ^{2} (u).}$$

  
• cn ( u ):
  $${\ displaystyle \ operatorname {cn} (u, m) \ approx \ operatorname {sech} (u)-{\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ tanh (u) \ operatorname {sech} (u).}$$

  
• dn ( u ):
  $${\ displaystyle \ operatorname {dn} (u, m) \ approx \ operatorname {sech} (u)+{\ frac {1} {4}} m '(\ sinh (u) \ cosh (u)+u) \ tanh (u) \ operatorname {sech} (u).}$$

  
• er ( u ):
  $${\ displaystyle \ operatorname {am} (u, m) \ approx \ operatorname {gd} (u)+{\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ operatorname {sech} (u).}$$

  

Fortsatte brøk

Forutsatt reelle tall med og nomen , med elliptisk modul . Hvis , hvor er den komplette elliptiske integralen av den første typen , holder den følgende fortsatte fraksjonsexpansjon${\ displaystyle a, p}$${\ displaystyle 0 <a <p}$ ${\ displaystyle q = e^{\ pi i \ tau}}$${\ displaystyle \ operatorname {Im} (\ tau)> 0}$ ${\ textstyle k (\ tau) = {\ sqrt {1-k '(\ tau)^{2}}} = (\ vartheta _ {10} (0; \ tau)/\ vartheta _ {00} (0 ; \ tau))^{2}}$${\ displaystyle K [\ tau] = K (k (\ tau))}}$${\ displaystyle K (x) = \ pi/2 \ cdot {} _ {2} F_ {1} (1/2,1/2; 1; x^{2})}$

${\ displaystyle {\ begin {align} & {\ frac {{\ textrm {dn}} \ left ((p/2-a) \ tau K \ left [{\ frac {p \ tau} {2}} \ høyre]; k \ venstre ({\ frac {p \ tau} {2}} \ høyre) \ høyre)} {\ sqrt {k '\ venstre ({\ frac {p \ tau} {2}} \ høyre) }}} = {\ frac {\ sum _ {n =-\ infty}^{\ infty} q^{p/2n^{2}+(p/2-a) n}} {\ sum _ {n =-\ infty}^{\ infty} (-1)^{n} q^{p/2n^{2}+(p/2-a) n}}} \\ [4pt] = {} &- 1+{\ frac {2} {1-}} {\ frac {q^{a}+q^{pa}} {1-q^{p}+}} {\ frac {(q^{a} +q^{2p-a}) (q^{a+p}+q^{pa})} {1-q^{3p}+}} {\ frac {q^{p} (q^{a }+q^{3p-a}) (q^{a+2p}+q^{pa})} {1-q^{5p}+}} {\ frac {q^{2p} (q^{ a}+q^{4p-a}) (q^{a+3p}+q^{pa})} {1-q^{7p}+}} \ ldots \ end {align}}}$