Sentralitet - Centrality

I grafteori og nettverksanalyse tildeler indikatorer for sentralitet tall eller rangeringer til noder i en graf som tilsvarer nettverksposisjonen. Søknadene inkluderer identifisering av de mest innflytelsesrike personene i et sosialt nettverk , viktige infrastrukturnoder på Internett eller urbane nettverk , superspredere av sykdom og hjernenettverk. Sentralitetskonsepter ble først utviklet i analyser av sosiale nettverk , og mange av begrepene som brukes for å måle sentralitet, gjenspeiler deres sosiologiske opprinnelse.

Definisjon og karakterisering av sentralitetsindekser

Sentralitetsindekser er svar på spørsmålet "Hva kjennetegner et viktig toppunkt?" Svaret er gitt i form av en virkelig verdi funksjon på hjørnene i en graf, der verdiene som produseres forventes å gi en rangering som identifiserer de viktigste nodene.

Ordet "betydning" har et stort antall betydninger, noe som fører til mange forskjellige definisjoner av sentralitet. To kategoriseringsordninger er foreslått. "Viktighet" kan tenkes i forhold til en type flyt eller overføring over nettverket. Dette gjør at sentraliteter kan klassifiseres etter hvilken type strøm de anser som viktige. "Viktighet" kan alternativt tenkes som involvering i nettverkets sammenheng. Dette gjør det mulig å klassifisere sentraliteter basert på hvordan de måler sammenheng. Begge disse tilnærmingene deler sentraliteter i forskjellige kategorier. En ytterligere konklusjon er at en sentralitet som er passende for en kategori ofte vil "ta feil" når den brukes på en annen kategori.

Mange, men ikke alle, sentralitetstiltak teller effektivt antall stier (også kalt turer) av en eller annen type som går gjennom et gitt toppunkt; tiltakene er forskjellige i hvordan de relevante turene defineres og telles. Begrensende hensyn til denne gruppen gir mulighet for taksonomi som plasserer mange sentraliteter i et spekter fra de som er opptatt av turer i lengde én ( gradersentralitet ) til uendelige turer ( egenvektorsentralitet ). Andre sentralitetstiltak, for eksempel mellom sentralitet, fokuserer ikke bare på generell tilkobling, men inntar posisjoner som er avgjørende for nettverkets tilkobling.

Karakterisering etter nettverksstrømmer

Et nettverk kan betraktes som en beskrivelse av stiene som noe flyter langs. Dette tillater en karakterisering basert på typen flyt og typen bane som er kodet av sentraliteten. En flyt kan være basert på overføringer, hvor hver udelelige vare går fra en node til en annen, som en pakkelevering som går fra leveringsstedet til klientens hus. Et annet tilfelle er seriell duplisering, der et element replikeres slik at både kilden og målet har det. Et eksempel er spredning av informasjon gjennom sladder, med informasjonen som spres på en privat måte og med både kilden og målnodene blir informert på slutten av prosessen. Den siste saken er parallell duplisering, med elementet duplisert til flere lenker samtidig, som en radiosending som gir den samme informasjonen til mange lyttere samtidig.

På samme måte kan banetypen begrenses til geodesikk (korteste stier), stier (ingen toppunkt blir besøkt mer enn én gang), stier (hjørner kan besøkes flere ganger, ingen kant krysses mer enn én gang) eller turer (hjørner og kanter kan besøkes/krysses flere ganger).

Karakterisering etter gangstruktur

En alternativ klassifisering kan utledes av hvordan sentraliteten er konstruert. Dette deler seg igjen i to klasser. Sentraliteter er enten radiale eller mediale. Radiale sentraliteter teller turer som starter/slutter fra det gitte toppunktet. Den grad og egenverdi centralities er eksempler på radiale centralities, telle antall turer av lengden av en eller lengde uendelig. Mediale sentraliteter teller turer som går gjennom det gitte toppunktet. Kanonisk eksempel er Freeman betweenness sentralitet, antallet av korteste veier som passerer gjennom det gitte toppunktet.

På samme måte kan tellingen registrere enten volumet eller lengden på turene. Volum er det totale antallet turer av den gitte typen. De tre eksemplene fra forrige avsnitt faller inn i denne kategorien. Lengde fanger avstanden fra det gitte toppunktet til de resterende toppunktene i grafen. Freemans nærhet sentralitet, den totale geodesiske avstanden fra et gitt toppunkt til alle andre hjørner, er det mest kjente eksemplet. Vær oppmerksom på at denne klassifiseringen er uavhengig av hvilken type gang man teller (dvs. gange, sti, bane, geodesikk).

Borgatti og Everett foreslår at denne typologien gir innsikt i hvordan man best kan sammenligne sentralitetstiltak. Sentraler plassert i samme boks i denne 2 × 2 -klassifiseringen er like nok til å lage troverdige alternativer; man kan rimelig sammenligne hvilken som er bedre for en gitt applikasjon. Tiltak fra forskjellige bokser er imidlertid kategorisk forskjellige. Enhver evaluering av relativ kondisjon kan bare skje innenfor rammen av forhåndsbestemmelse av hvilken kategori som er mer anvendelig, noe som gjør sammenligningen uavhengig.

Radialvolum sentraliteter eksisterer på et spekter

Karakteriseringen etter gangstruktur viser at nesten alle sentraliteter i stor bruk er radialvolummål. Disse koder for troen på at et toppunkts sentralitet er en funksjon av sentraliteten til toppunktene det er assosiert med. Sentraliteter skiller seg ut fra hvordan assosiasjon defineres.

Bonacich viste at hvis assosiasjon er definert i form av turer , så kan en familie med sentraliteter defineres basert på turlengden som er vurdert. Gradsentralitet teller turer i lengde én, mens egenverdi sentralitet teller turer i lengde uendelig. Alternative definisjoner av assosiasjon er også rimelige. Alpha -sentralitet gjør at hjørner kan ha en ekstern påvirkningskilde. Estradas subgrafsentralitet foreslår bare å telle lukkede stier (trekanter, firkanter, etc.).

Hjertet i slike tiltak er observasjonen av at kreftene i grafens tilstøtningsmatrise gir antall turer av lengde gitt av denne kraften. På samme måte er matrisens eksponensial også nært knyttet til antall turer i en gitt lengde. En innledende transformasjon av adjacency -matrisen tillater en annen definisjon av typen gange som telles. Under begge tilnærminger kan sentraliteten til et toppunkt uttrykkes som en uendelig sum

{\ displaystyle \ sum _ {k = 0}^{\ infty} A_ {R}^{k} \ beta^{k}}

for matrisekrefter eller

{\ displaystyle \ sum _ {k = 0}^{\ infty} {\ frac {(A_ {R} \ beta)^{k}} {k!}}}

for matriseeksponensialer, hvor

${\ displaystyle k}$ er turlengde,
${\ displaystyle A_ {R}}$ er den transformerte adjacensmatrisen, og
${\ displaystyle \ beta}$ er en rabattparameter som sikrer konvergens av summen.

Bonacichs tiltaksfamilie transformerer ikke adjacensmatrisen. Alpha sentralitet erstatter adjacency matrisen med sin resolvent . Subgrafsentralitet erstatter adjacensmatrisen med sitt spor. En oppsiktsvekkende konklusjon er at alle slike tilnærminger har en felles begrensende oppførsel, uavhengig av den innledende transformasjonen av adjasensmatrisen. Når det nærmer seg null, konvergerer indeksene til graders sentralitet . Når den nærmer seg sin maksimale verdi, konvergerer indeksene til egenverdi sentralitet . ${\ displaystyle \ beta}$ ${\ displaystyle \ beta}$

Spillteoretisk sentralitet

Felles trekk ved de fleste av de ovennevnte standardmålene er at de vurderer viktigheten av en node ved bare å fokusere på rollen som en node spiller av seg selv. Imidlertid er en slik tilnærming i mange applikasjoner utilstrekkelig på grunn av synergier som kan oppstå hvis funksjonen til noder vurderes i grupper.

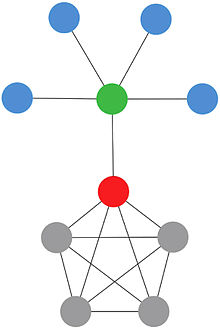
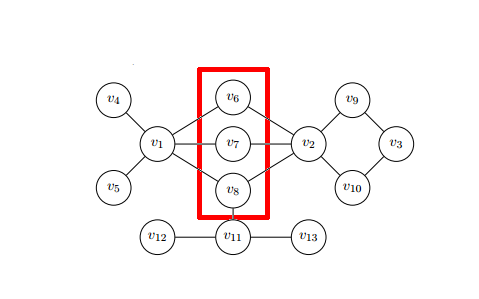
Tenk for eksempel på problemet med å stoppe en epidemi. Hvilke noder bør vi vaksinere når vi ser på bildet over nettverket ovenfor? Basert på tidligere beskrevne tiltak, ønsker vi å gjenkjenne noder som er de viktigste i sykdomsspredning. Tilnærminger som bare er basert på sentraliteter, som fokuserer på individuelle trekk ved noder, er kanskje ikke en god idé. Noder i den røde firkanten, individuelt kan ikke stoppe sykdommen sprer seg, men vurderer dem som en gruppe, vi tydelig se at de kan stoppe sykdommen hvis den har startet i noder , og . Spillteoretiske sentraliteter prøver å konsultere beskrevne problemer og muligheter ved å bruke verktøy fra spillteori. Tilnærmingen som foreslås i bruker Shapley -verdien . På grunn av tidskompleksiteten i Shapley-verdiberegningen, er de fleste innsatsene på dette domenet drevet til å implementere nye algoritmer og metoder som er avhengige av en særegen topologi i nettverket eller en spesiell karakter av problemet. En slik tilnærming kan føre til å redusere tidskompleksiteten fra eksponentiell til polynom. ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {4}}$ ${\ displaystyle v_ {5}}$

På samme måte bruker løsningskonseptet autoritetsdistribusjon () Shapley-Shubik-effektindeksen , i stedet for Shapley-verdien , for å måle den bilaterale direkte innflytelsen mellom spillerne. Fordelingen er faktisk en type egenvektorsentralitet. Den brukes til å sortere store dataobjekter i Hu (2020), for eksempel rangering av amerikanske høyskoler.

Viktige begrensninger

Sentralitetsindekser har to viktige begrensninger, den ene åpenbare og den andre subtile. Den åpenbare begrensningen er at en sentralitet som er optimal for en applikasjon ofte er suboptimal for en annen applikasjon. Faktisk, hvis dette ikke var slik, ville vi ikke trengt så mange forskjellige sentraliteter. En illustrasjon av dette fenomenet er gitt av Krackhardt -dragediagrammet , hvor tre forskjellige forestillinger om sentralitet gir tre forskjellige valg av det mest sentrale toppunktet.

Den mer subtile begrensningen er den vanlige feilen at toppunktssentralitet indikerer den relative viktigheten av hjørner. Sentralitetsindekser er eksplisitt designet for å produsere en rangering som tillater indikasjon av de viktigste hjørnene. Dette gjør de godt, under begrensningen som nettopp er nevnt. De er ikke designet for å måle påvirkning av noder generelt. Nylig har nettverksfysikere begynt å utvikle nodepåvirkningsberegninger for å løse dette problemet.

Feilen er todelt. For det første, en rangering ordner bare hjørner etter betydning, den kvantifiserer ikke forskjellen i betydning mellom forskjellige nivåer av rangeringen. Dette kan dempes ved å bruke Freeman -sentralisering på det aktuelle sentralitetstiltaket, som gir litt innsikt i viktigheten av noder avhengig av forskjellene i sentraliseringspoengene deres. Videre gjør Freeman -sentralisering det mulig å sammenligne flere nettverk ved å sammenligne deres høyeste sentraliseringspoeng. Denne tilnærmingen er imidlertid sjelden sett i praksis.

For det andre generaliserer ikke nødvendigvis funksjonene som (riktig) identifiserer de viktigste hjørnene i et gitt nettverk/program til de resterende hjørnene. For de fleste andre nettverksnoder kan rangeringen være meningsløs. Dette forklarer hvorfor for eksempel bare de første resultatene av et Google bildesøk vises i en rimelig rekkefølge. Sidetanken er et svært ustabilt mål, som viser hyppige rangomvendelser etter små justeringer av hoppeparameteren.

Selv om sentralitetsindeksene ikke kan generaliseres til resten av nettverket i begynnelsen kan virke kontraintuitive, følger det direkte av definisjonene ovenfor. Komplekse nettverk har heterogen topologi. I den grad det optimale målet er avhengig av nettverksstrukturen til de viktigste toppunktene, er et mål som er optimalt for slike hjørner sub-optimalt for resten av nettverket.

Gradsentralitet

Eksempler på A) Sentralitet mellom sentralitet , B) Nærhetssentralitet , C) Eigenvektorsentralitet , D) Gradsentralitet , E) Harmonisk sentralitet og F) Katz -sentralitet i samme graf.

Historisk sett først og konseptuelt enklest er gradersentralitet , som er definert som antall koblinger som skjer på en node (dvs. antall bindinger som en node har). Graden kan tolkes i form av den umiddelbare risikoen for en node for å fange det som strømmer gjennom nettverket (for eksempel et virus eller informasjon). Når det gjelder et rettet nettverk (der bånd har retning), definerer vi vanligvis to separate mål for graders sentralitet, nemlig uavhengig og utvendig . Følgelig er indegree en telling av antall bånd som er rettet til noden og utgrad er antallet bånd som noden retter til andre. Når bånd er knyttet til noen positive aspekter som vennskap eller samarbeid, tolkes uavhengighet ofte som en form for popularitet, og utdannelse som fellesskap.

Gradsentraliteten til et toppunkt , for en gitt graf med hjørner og kanter, er definert som ${\ displaystyle v}$ ${\ displaystyle G: = (V, E)}$ ${\ displaystyle | V |}$ ${\ displaystyle | E |}$

{\ displaystyle C_ {D} (v) = \ deg (v)}

Beregning av graders sentralitet for alle nodene i en graf tar en tett adjacensmatrisepresentasjon av grafen, og for kanter tar den en sparsom matrisepresentasjon . ${\ displaystyle \ Theta (V^{2})}$ ${\ displaystyle \ Theta (E)}$

Definisjonen av sentralitet på nodenivå kan utvides til hele grafen, i så fall snakker vi om grafsentralisering . La være noden med høyeste grad sentralitet i . La være den -node tilkoblede grafen som maksimerer følgende mengde (med å være noden med høyeste grad sentralitet i ): ${\ displaystyle v*}$ ${\ displaystyle G}$ ${\ displaystyle X: = (Y, Z)}$ ${\ displaystyle | Y |}$ ${\ displaystyle y*}$ ${\ displaystyle X}$

{\ displaystyle H = \ sum _ {j = 1}^{| Y |} [C_ {D} (y*)-C_ {D} (y_ {j})]}}

Tilsvarende er graden sentralisering av grafen som følger: ${\ displaystyle G}$

{\ displaystyle C_ {D} (G) = {\ frac {\ sum _ {i = 1}^{| V |} [C_ {D} (v*)-C_ {D} (v_ {i})] } {H}}}

Verdien av maksimeres når grafen inneholder en sentral node som alle andre noder er koblet til (et stjernediagram ), og i dette tilfellet ${\ displaystyle H}$ ${\ displaystyle X}$

{\ displaystyle H = (n-1) \ cdot ((n-1) -1) = n^{2} -3n+2.}

Så, for en hvilken som helst graf ${\ displaystyle G: = (V, E),}$

{\ displaystyle C_ {D} (G) = {\ frac {\ sum _ {i = 1}^{| V |} [C_ {D} (v*)-C_ {D} (v_ {i})]] } {| V |^{2} -3 | V | +2}}}

Et nytt omfattende globalt mål for graden sentralitet ved navn Tendency to Make Hub (TMH) definerer også som følger:

{\ displaystyle TMK = {\ frac {\ sum _ {i = 1}^{| V |} [deg (v)]^{2}} {\ sum _ {i = 1}^{| V |} deg (v)}}}

hvor TMH øker ved utseende av graders sentralitet i nettverket.

Nærhet sentralitet

I en tilkoblet graf er normalisert nærhetssentralitet (eller nærhet ) til en node gjennomsnittlig lengde på den korteste banen mellom noden og alle andre noder i grafen. Så jo mer sentral en node er, desto nærmere er den alle andre noder.

Nærhet ble definert ved Alex Bavelas (1950) som den resiproke verdi av den farness , som er:

{\ displaystyle C (x) = {\ frac {1} {\ sum _ {y} d (x, y)}}}

hvor er avstanden mellom hjørner og . Men når man snakker om nærhetssentralitet, refererer folk vanligvis til den normaliserte formen, vanligvis gitt av den forrige formelen multiplisert med , hvor er antall noder i grafen. Denne justeringen tillater sammenligninger mellom grafer i forskjellige størrelser. ${\ displaystyle d (x, y)}$ ${\ displaystyle x}$ ${\ displaystyle y}$ ${\ displaystyle N-1}$ ${\ displaystyle N}$

Å ta avstander fra eller til alle andre noder er irrelevant i ikke -dirigerte grafer, mens det kan gi helt forskjellige resultater i dirigerte grafer (f.eks. Et nettsted kan ha høy nærhetssentralitet fra utgående lenke, men lav nærhetssentralitet fra innkommende lenker).

Harmonisk sentralitet

I en (ikke nødvendigvis tilkoblet) graf reverserer den harmoniske sentraliteten summen og gjensidige operasjoner i definisjonen av nærhetssentralitet:

{\ displaystyle H (x) = \ sum _ {y \ neq x} {\ frac {1} {d (x, y)}}}

hvor hvis det ikke er noen vei fra til . Harmonisk sentralitet kan normaliseres ved å dividere med , hvor er antall noder i grafen. ${\ displaystyle 1/d (x, y) = 0}$ ${\ displaystyle x}$ ${\ displaystyle y}$ ${\ displaystyle N-1}$ ${\ displaystyle N}$

Harmonisk sentralitet ble foreslått av Marchiori og Latora (2000) og deretter uavhengig av Dekker (2005), ved å bruke navnet "verdsatt sentralitet" og av Rochat (2009).

Mellom sentralitet

Nyanse (fra rødt = 0 til blått = maks) viser noden mellom.

Betweenness er et sentralitetsmål på et toppunkt i en graf (det er også kant mellom dem, som ikke diskuteres her). Sentralitet mellom kvantifiserer antall ganger en node fungerer som en bro langs den korteste banen mellom to andre noder. Den ble introdusert som et tiltak for å kvantifisere kontrollen av et menneske på kommunikasjonen mellom andre mennesker i et sosialt nettverk av Linton Freeman . I hans oppfatning har hjørner som har stor sannsynlighet for å forekomme på en tilfeldig valgt korteste vei mellom to tilfeldig valgte hjørner en høy mellomhet.

Mellompunktet til et toppunkt i en graf med hjørner beregnes som følger: ${\ displaystyle v}$ ${\ displaystyle G: = (V, E)}$ ${\ displaystyle V}$

For hvert par hjørner ( r , t ), beregner du de korteste banene mellom dem.
Bestem brøkdelen av de korteste banene som passerer gjennom det aktuelle toppunktet (her, toppunkt v ) for hvert par hjørner ( s , t ).
Sum denne brøkdelen over alle par av hjørner ( s , t ).

Mer kompakt kan mellomverdien representeres som:

{\ displaystyle C_ {B} (v) = \ sum _ {s \ neq v \ neq t \ in V} {\ frac {\ sigma _ {st} (v)} {\ sigma _ {st}}}}

hvor er totalt antall korteste stier fra node til node og er antallet av de banene som passerer gjennom . Mellomhendigheten kan normaliseres ved å dele gjennom antall par av hjørner som ikke inkluderer v , som for dirigerte grafer er og for uorienterte grafer er . For eksempel, i en ikke -rettet stjernediagram , ville midtpunktet (som finnes i alle mulige korteste veier) ha en mellomhet på (1, hvis den er normalisert) mens bladene (som finnes på ingen korteste stier) vil ha en mellomrom på 0. ${\ displaystyle \ sigma _ {st}}$ ${\ displaystyle s}$ ${\ displaystyle t}$ ${\ displaystyle \ sigma _ {st} (v)}$ ${\ displaystyle v}$ ${\ displaystyle (n-1) (n-2)}$ ${\ displaystyle (n-1) (n-2)/2}$ ${\ displaystyle (n-1) (n-2)/2}$

Fra et beregningsaspekt innebærer både sentralitet og nærhet sentralitet for alle hjørner i en graf å beregne de korteste banene mellom alle parene av hjørner på en graf, noe som krever tid med Floyd - Warshall -algoritmen . På sparsomme grafer kan imidlertid Johnsons algoritme være mer effektiv og ta tid. For uvektede grafer kan beregningene gjøres med Brandes 'algoritme som tar tid. Normalt antar disse algoritmene at grafer er ustyrte og forbundet med tillatelse til sløyfer og flere kanter. Når man spesifikt håndterer nettverksgrafer, er grafer ofte uten sløyfer eller flere kanter for å opprettholde enkle relasjoner (hvor kanter representerer forbindelser mellom to personer eller hjørner). I dette tilfellet vil bruk av Brandes 'algoritme dele de endelige sentralitetspoengene med 2 for å ta hensyn til at hver korteste bane telles to ganger. ${\ displaystyle O (V^{3})}$ ${\ displaystyle O (V^{2} \ log V+VE)}$ ${\ displaystyle O (VE)}$

Eigenvektors sentralitet

Eigenvektorsentralitet (også kalt egensentralitet ) er et mål på påvirkning av en node i et nettverk . Den tildeler relative poengsummer til alle noder i nettverket basert på konseptet om at tilkoblinger til noder med høy poengsum bidrar mer til poengsummen til den aktuelle noden enn like tilkoblinger til noder med lav poengsum. Google 's Pagerank og Katz sentralitet er varianter av egenvektor sentralitet.

Bruke adjasensmatrisen for å finne egenvektorsentralitet

For en gitt graf med antall hjørner la være adjasensmatrisen , dvs. hvis toppunktet er knyttet til toppunktet , og ellers. Den relative sentralitetspoengsummen til toppunktet kan defineres som: ${\ displaystyle G: = (V, E)}$ ${\ displaystyle | V |}$ ${\ displaystyle A = (a_ {v, t})}$ ${\ displaystyle a_ {v, t} = 1}$ ${\ displaystyle v}$ ${\ displaystyle t}$ ${\ displaystyle a_ {v, t} = 0}$ ${\ displaystyle v}$

{\ displaystyle x_ {v} = {\ frac {1} {\ lambda}} \ sum _ {t \ i M (v)} x_ {t} = {\ frac {1} {\ lambda}} \ sum _ {t \ i G} a_ {v, t} x_ {t}}

hvor er et sett av naboene til og er en konstant. Med en liten omleiring dette kan omskrives i vektornotasjonen som i egenvektoren ligning ${\ displaystyle M (v)}$ ${\ displaystyle v}$ ${\ displaystyle \ lambda}$

{\ displaystyle \ mathbf {Ax} = {\ lambda} \ mathbf {x}}

Generelt vil det være mange forskjellige egenverdier som det finnes en egenvektorløsning uten null. Siden oppføringene i adjasensmatrisen er ikke-negative, er det en unik største egenverdi, som er reell og positiv, etter Perron-Frobenius-setningen . Denne største egenverdien resulterer i ønsket sentralitetsmål. Den komponenten av den tilhørende egenvektor da gir den relative viktig stillingen av toppunktet i nettverket. Egenvektoren er bare definert opp til en felles faktor, så bare forholdene mellom sentralitetene i toppunktene er godt definert. For å definere en absolutt score må man normalisere egenvektoren, f.eks. Slik at summen over alle toppunktene er 1 eller det totale antallet hjørner n . Kraft iterasjon er en av mange egenverdi algoritmer som kan brukes til å finne denne dominerende egenvektoren. Videre kan dette generaliseres slik at oppføringene i A kan være reelle tall som representerer forbindelsesstyrker, som i en stokastisk matrise . ${\ displaystyle \ lambda}$ ${\ displaystyle v^{th}}$ ${\ displaystyle v}$

Katz sentralitet

Katz sentralitet er en generalisering av gradssentralitet. Gradsentralitet måler antall direkte naboer, og Katz sentralitet måler antall alle noder som kan kobles gjennom en bane, mens bidrag fra fjerne noder straffes. Matematisk er det definert som

{\ displaystyle x_ {i} = \ sum _ {k = 1}^{\ infty} \ sum _ {j = 1}^{N} \ alpha^{k} (A^{k}) _ {ji} }

hvor er en dempningsfaktor i . ${\ displaystyle \ alpha}$ ${\ displaystyle (0,1)}$

Katz sentralitet kan sees på som en variant av egenvektorsentralitet. En annen form for Katz sentralitet er

{\ displaystyle x_ {i} = \ alpha \ sum _ {j = 1}^{N} a_ {ij} (x_ {j} +1).}

Sammenlignet med uttrykket egenvektorsentralitet, erstattes av ${\ displaystyle x_ {j}}$ ${\ displaystyle x_ {j} +1.}$

Det er vist at den viktigste egenvektoren (assosiert med den største egenverdien av , adjasensmatrisen) er grensen for Katz sentralitet når det nærmer seg nedenfra. ${\ displaystyle A}$ ${\ displaystyle \ alpha}$ ${\ displaystyle {\ tfrac {1} {\ lambda}}}$

Sentralt i siderangering

PageRank tilfredsstiller følgende ligning

{\ displaystyle x_ {i} = \ alpha \ sum _ {j} a_ {ji} {\ frac {x_ {j}} {L (j)}}+{\ frac {1- \ alpha} {N}} ,}

hvor

{\ displaystyle L (j) = \ sum _ {i} a_ {ji}}

er antall naboer til noden (eller antall utgående lenker i en dirigert graf). Sammenlignet med egenvektorsentralitet og Katz -sentralitet, er en stor forskjell skaleringsfaktoren . En annen forskjell mellom PageRank og egenvektorsentralitet er at PageRank -vektoren er en egenvektor til venstre (merk at faktoren har indekser reversert). ${\ displaystyle j}$ ${\ displaystyle L (j)}$ ${\ displaystyle a_ {ji}}$

Perkoleringssentralitet

Det finnes en rekke sentralitetstiltak for å bestemme viktigheten av en enkelt node i et komplekst nettverk. Imidlertid kvantifiserer disse tiltakene viktigheten av en node rent topologisk, og verdien av noden avhenger ikke av nodens 'tilstand' på noen måte. Den forblir konstant uavhengig av nettverksdynamikk. Dette gjelder selv for de veide målene mellom mål. Imidlertid kan en node veldig godt være sentralt plassert når det gjelder sentralitet mellom sentraler eller et annet sentralitetstiltak, men kan ikke være 'sentralt' plassert i sammenheng med et nettverk der det er perkolasjon. Perkolasjon av en 'smitte' forekommer i komplekse nettverk i en rekke scenarier. For eksempel kan virus- eller bakteriell infeksjon spre seg over sosiale nettverk av mennesker, kjent som kontaktnettverk. Spredning av sykdom kan også vurderes på et høyere abstraksjonsnivå, ved å vurdere et nettverk av byer eller befolkningssentre, forbundet med vei, jernbane eller flyforbindelser. Datavirus kan spre seg over datanettverk. Rykter eller nyheter om forretningstilbud og avtaler kan også spre seg via sosiale nettverk av mennesker. I alle disse scenariene sprer en 'smitte' seg over koblingene til et komplekst nettverk, og endrer 'tilstandene' til nodene etter hvert som de sprer seg, enten gjenvinnbart eller på annen måte. For eksempel, i et epidemiologisk scenario, går individer fra "mottagelig" til "infisert" tilstand når infeksjonen sprer seg. Statene de enkelte nodene kan ta i eksemplene ovenfor kan være binære (for eksempel mottatt/ikke mottatt nyhet), diskrete (mottagelige/infiserte/gjenopprettede) eller til og med kontinuerlige (for eksempel andelen infiserte mennesker i en by ), mens smitten sprer seg. Felles trekk i alle disse scenariene er at smittespredning resulterer i endring av nodetilstander i nettverk. Perkoleringssentralitet (PC) ble foreslått med dette i tankene, som spesifikt måler viktigheten av noder når det gjelder å hjelpe perkolasjonen gjennom nettverket. Dette tiltaket ble foreslått av Piraveenan et al.

Perkoleringssentralitet er definert for en gitt node, på et gitt tidspunkt, som andelen "perkulerte stier" som går gjennom denne noden. En 'perkolert bane' er en korteste bane mellom et par noder, der kildenoden er perkolert (f.eks. Infisert). Målnoden kan være perkolert eller ikke-perkolert, eller i en delvis perkolert tilstand.

{\ displaystyle PC^{t} (v) = {\ frac {1} {N-2}} \ sum _ {s \ neq v \ neq r} {\ frac {\ sigma _ {sr} (v)} {\ sigma _ {sr}}} {\ frac {{x^{t}} _ {s}} {{\ sum {[{x^{t}} _ {i}}]}-{x^{ TV}}}}

hvor er totalt antall korteste stier fra node til node og er antallet av de banene som passerer gjennom . Perkolasjonstilstanden til noden til enhver tid er angitt med og to spesielle tilfeller er når som indikerer en ikke-perkolert tilstand på et tidspunkt, mens når som indikerer en fullstendig perkolert tilstand til enhver tid . Verdiene i mellom indikerer delvis perkulerte stater (f.eks. I et nettverk av townships vil dette være prosentandelen av mennesker smittet i byen). ${\ displaystyle \ sigma _ {sr}}$ ${\ displaystyle s}$ ${\ displaystyle r}$ ${\ displaystyle \ sigma _ {sr} (v)}$ ${\ displaystyle v}$ ${\ displaystyle i}$ ${\ displaystyle t}$ ${\ displaystyle {x^{t}} _ {i}}$ ${\ displaystyle {x^{t}} _ {i} = 0}$ ${\ displaystyle t}$ ${\ displaystyle {x^{t}} _ {i} = 1}$ ${\ displaystyle t}$

De vedlagte vekter til perkoleringsbanene avhenger av perkoleringsnivåene som er tilordnet kildenodene, basert på forutsetningen at jo høyere perkolasjonsnivået til en kildeknute er, desto viktigere er banene som stammer fra den noden. Noder som ligger på de korteste veiene som stammer fra sterkt perkolerte noder, er derfor potensielt viktigere for perkolasjonen. Definisjonen av PC kan også utvides til også å omfatte målnodevekter. Beregninger av perkoleringssentralitet løper i tide med en effektiv implementering som er tatt i bruk fra Brandes raske algoritme, og hvis beregningen må ta i betraktning målnoder, er tiden i verste fall . ${\ displaystyle O (NM)}$ ${\ displaystyle O (N^{3})}$

Kryss-klikk-sentralitet

Kryss-klikk-sentralitet for en enkelt node i en kompleks graf bestemmer tilkoblingen av en node til forskjellige klikk . En node med høy kryss-klikk-tilkobling gjør det lettere å spre informasjon eller sykdom i en graf. Cliques er undergrafer der hver node er koblet til hver annen node i clique. Kryss-klikk-tilkoblingen til en node for en gitt graf med hjørner og kanter, er definert som hvor er antallet klikk som toppunktet tilhører. Dette tiltaket ble brukt i, men ble først foreslått av Everett og Borgatti i 1998 hvor de kalte det sentralitet for overlapping mellom klikk. ${\ displaystyle v}$ ${\ displaystyle G: = (V, E)}$ ${\ displaystyle | V |}$ ${\ displaystyle | E |}$ ${\ displaystyle X (v)}$ ${\ displaystyle X (v)}$ ${\ displaystyle v}$

Freeman sentralisering

Den sentralisering av et hvilket som helst nettverk er et mål på hvor sin sentrale mest sentrale node er i forhold til hvordan sentral alle de andre nodene er. Sentraliseringstiltak deretter (a) beregner summen i forskjeller i sentralitet mellom den mest sentrale noden i et nettverk og alle andre noder; og (b) dele denne mengden med den teoretisk største slike sum av forskjeller i ethvert nettverk av samme størrelse. Dermed kan hvert sentralitetstiltak ha sitt eget sentraliseringstiltak. Definert formelt, om det er et sentralitetsmål for punkt , om det er det største målet i nettverket, og hvis: ${\ displaystyle C_ {x} (p_ {i})}$ ${\ displaystyle i}$ ${\ displaystyle C_ {x} (s _ {*})}$

{\ displaystyle \ max \ sum _ {i = 1}^{N} C_ {x} (p _ {*})-C_ {x} (p_ {i})}}

er den største summen av forskjeller i punktsentralitet for en hvilken som helst graf med samme antall noder, så er sentraliseringen av nettverket: ${\ displaystyle C_ {x}}$

{\ displaystyle C_ {x} = {\ frac {\ sum _ {i = 1}^{N} C_ {x} (p _ {*})-C_ {x} (p_ {i})} {\ max \ sum _ {i = 1}^{N} C_ {x} (p _ {*})-C_ {x} (p_ {i})}}}}

Konseptet skyldes Linton Freeman .

Ulikheter basert sentralitetstiltak

I det illustrerte nettverket er grønne og røde noder de mest forskjellige fordi de ikke deler naboer mellom dem. Så den grønne bidrar mer til sentraliteten til den røde enn den grå, fordi den røde bare kan få tilgang til de blå gjennom den grønne, og de grå nodene er overflødige for den røde, fordi den kan få tilgang direkte til hver grå node uten mellomledd.

For å oppnå bedre resultater i rangeringen av nodene til et gitt nettverk, brukes ulikhetstiltak (spesifikk for teorien om klassifisering og data mining) for å berike sentralitetstiltakene i komplekse nettverk. Dette er illustrert med egenvektorsentralitet , og beregner sentraliteten til hver node gjennom løsningen av egenverdi -problemet

{\ displaystyle W \ mathbf {c} = \ lambda \ mathbf {c}}

hvor (koordinat-til-koordinat produkt) og er en vilkårlig ulikhetsmatrise , definert gjennom et ulikt tiltak, f.eks. Jaccard ulikhet gitt av ${\ displaystyle W_ {ij} = A_ {ij} D_ {ij}}$ ${\ displaystyle D_ {ij}}$

{\ displaystyle D_ {ij} = 1-{\ dfrac {| V^{+} (i) \ cap V^{+} (j) |} {| V^{+} (i) \ cup V^{ +} (j) |}}}

Hvor dette tiltaket tillater oss å kvantifisere det topologiske bidraget (det er derfor det kalles bidragsentralitet) for hver node til sentraliteten til en gitt node, med større vekt/relevans, har disse noder med større ulikhet, siden disse tillater den gitte noden tilgang til noder som de ikke selv kan få tilgang til direkte.

Er bemerkelsesverdig som er ikke-negativ fordi og er ikke-negative matriser, så vi kan bruke Perron-Frobenius-setningen for å sikre at problemet ovenfor har en unik løsning for λ = λ _max med c non-negative, slik at vi kan utlede sentraliteten til hver node i nettverket. Derfor er sentraliteten til i-noden ${\ displaystyle W}$ ${\ displaystyle A}$ ${\ displaystyle D}$

{\ displaystyle c_ {i} = {\ dfrac {1} {n}} \ sum _ {j = 1}^{n} W_ {ij} c_ {j}, \, \, \, \, \, \ , i = 1, \ cdots, n}

hvor er antallet noder i nettverket. Flere ulikhetstiltak og nettverk ble testet for å oppnå forbedrede resultater i de studerte tilfellene. ${\ displaystyle n}$

Se også

Notater og referanser

Videre lesning

Koschützki, D .; Lehmann, KA; Peeters, L .; Richter, S .; Tenfelde-Podehl, D. og Zlotowski, O. (2005) Sentralitetsindekser. I Brandes, U. og Erlebach, T. (red.) Nettverksanalyse: Methodological Foundations , s. 16–61, LNCS 3418, Springer-Verlag.

Languages

In other projects