Hasse diagram - Hasse diagram

For ikke å forveksle med Hess -diagram .
Den kraft sett fra et to-element set bestilt av inkludering

I rekkefølge teori , en Hasse diagram ( / h æ s ə / ; tysk: [hasə] ) er en type matematisk diagram som benyttes til å representere en endelig delvis ordnet sett , i form av en tegning av den transitive reduksjon . Konkret, for et delvis ordnet sett (S, ≤) representerer en hvert element av S som et toppunkt i planet og tegner et linjestykke eller en kurve som går oppover fra x til y når y dekker x (det vil si når x ≤ y og det er ingen z slik at x ≤ z ≤ y ). Disse kurvene kan krysse hverandre, men må ikke berøre andre hjørner enn endepunktene. Et slikt diagram, med merkede hjørner, bestemmer unikt dens delvise rekkefølge.

Diagrammene er oppkalt etter Helmut Hasse (1898–1979); ifølge Garrett Birkhoff  ( 1948 ), er de såkalte på grunn av den effektive bruken Hasse gjorde av dem. Imidlertid var Hasse ikke den første som brukte disse diagrammene. Ett eksempel som gikk før Hasse, finnes i Henri Gustav Vogt ( 1895 ). Selv om Hasse -diagrammer opprinnelig ble utviklet som en teknikk for å lage tegninger av delvis ordnede sett for hånd, har de nylig blitt opprettet automatisk ved hjelp av graftegningsteknikker .

Uttrykket "Hasse -diagram" kan også referere til den transitive reduksjonen som en abstrakt rettet asyklisk graf , uavhengig av tegning av den grafen, men denne bruken unngås her.

Diagramdesign

Selv om Hasse -diagrammer er enkle så vel som intuitive verktøy for å håndtere endelige poseter , viser det seg å være ganske vanskelig å tegne "gode" diagrammer. Årsaken er at det generelt vil være mange mulige måter å tegne et Hasse -diagram for en gitt poset. Den enkle teknikken med å bare begynne med de minimale elementene i en ordre og deretter tegne større elementer trinnvis gir ofte ganske dårlige resultater: symmetrier og intern struktur av ordren går lett tapt.

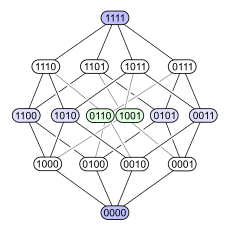
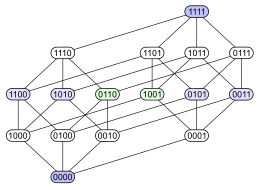
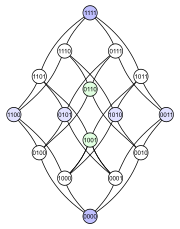
Følgende eksempel viser problemet. Tenk på kraftsettet til et sett med 4 elementer bestilt ved inkludering . Nedenfor er fire forskjellige Hasse -diagrammer for denne delordren. Hvert delsett har en node merket med en binær koding som viser om et bestemt element er i delsettet (1) eller ikke (0):

Hypercubeorder binær.svg     Hypercubecubes binary.svg     Hypercubestar binary.svg     Hypercubematrix binary.svg

Det første diagrammet gjør det klart at effektsettet er en gradert poset . Det andre diagrammet har samme gradert struktur, men ved å gjøre noen kanter lengre enn andre, understreker det at den 4-dimensjonale kuben er en kombinatorisk forening av to tredimensjonale kuber, og at et tetraeder ( abstrakt 3-polytop ) på samme måte fusjonerer to trekanter ( abstrakte 2-polytoper ). Det tredje diagrammet viser noe av strukturens indre symmetri. I det fjerde diagrammet er hjørnene arrangert som elementene i en 4 × 4 matrise .

Oppover planaritet

Hovedartikkel: Oppadgående plantegning
Dette Hasse -diagrammet over gitteret til undergruppene i dihedralgruppen Dih 4 har ingen kryssende kanter.

Hvis en delvis rekkefølge kan tegnes som et Hasse -diagram der det ikke krysses to kanter, sies det at dekkingsgrafen er plan oppover . En rekke resultater om oppadgående planaritet og om kryssingsfri Hasse-diagramkonstruksjon er kjent:

  • Hvis den delrekkefølgen som skal tegnes er et gitter , kan den trekkes uten kryss hvis og bare hvis den har bestillingsdimensjon på høyst to. I dette tilfellet kan en ikke-kryssende tegning bli funnet ved å utlede kartesiske koordinater for elementene fra deres posisjoner i de to lineære ordrene som realiserer ordredimensjonen, og deretter rotere tegningen mot klokken i en 45-graders vinkel.
  • Hvis delordenen har høyst ett minimalt element , eller det har maksimalt ett maksimalt element , kan det testes i lineær tid om det har et ikke-kryssende Hasse-diagram.
  • Det er NP-komplett å avgjøre om en delvis ordre med flere kilder og vasker kan tegnes som et kryssfritt Hasse-diagram. Å finne et kryssingsfritt Hasse-diagram kan imidlertid fastsettes med parametere når det parametreres av antall artikulasjonspunkter og trikoblede komponenter i den transitive reduksjonen av delordenen .
  • Hvis y -koordinatene til elementene i en delordre er spesifisert, kan et kryssfritt Hasse -diagram som respekterer disse koordinatoppgavene bli funnet i lineær tid, hvis et slikt diagram eksisterer. Spesielt hvis inndataposisjonen er en gradert poset , er det mulig å bestemme i lineær tid om det er et kryssfritt Hasse-diagram der høyden til hvert toppunkt er proporsjonal med dets rang.

UML -notasjon

Uttrykker eksemplet med standard UML -arvskontakter. Hvert sett er et distinkt objekt (standard UML -bokser er rektangulære).

Standarddiagrammet for en kjede av inneslutninger er UML -klassen , som forbinder sett etter arverelasjonen. Illustrasjonen viser en nestet settsamling , C :

B = {♠, ♥, ♦, ♣};     B 1 = {♠, ♥};   B 2 = {♦, ♣};   B 3 = {♣};
C = { B , B 1 , B 2 , B 3 }.

Merknader

Referanser

Eksterne linker