Gibbs fenomen - Gibbs phenomenon

I matematikk er Gibbs -fenomenet, oppdaget av Henry Wilbraham  ( 1848 ) og gjenoppdaget av J. Willard Gibbs  ( 1899 ), den særegne måten Fourier -serien av en stykkevis kontinuerlig differensierbar periodisk funksjon oppfører seg ved et hopp -diskontinuitet . Den n- te partielle sum av Fourier-serien har store svingninger i nærheten av hoppet, noe som kan øke den maksimale av den partielle sum som ligger over selve funksjonen. Overskridelsen dør ikke ut når n øker, men nærmer seg en begrenset grense. Denne oppførselen ble også observert av eksperimentelle fysikere, men antas å skyldes ufullkommenheter i måleapparatet.

Dette er en årsak til at det ringer gjenstander i signalbehandling .

Beskrivelse

Funksjonell tilnærming av firkantbølge ved hjelp av 5 harmoniske

Funksjonell tilnærming av firkantbølge ved hjelp av 25 harmoniske

Funksjonell tilnærming av firkantbølge ved hjelp av 125 harmoniske

Gibbs -fenomenet innebærer både det faktum at Fourier summerer overskridelse ved et hopp -diskontinuitet , og at dette overskridelsen ikke dør ut etter hvert som flere termer legges til summen.

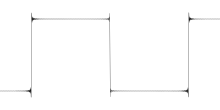
De tre bildene til høyre demonstrerer fenomenet for en firkantbølge (av høyde ) hvis Fourier -ekspansjon er ${\ displaystyle \ pi /4}$

${\ displaystyle \ sin (x)+{\ frac {1} {3}} \ sin (3x)+{\ frac {1} {5}} \ sin (5x)+\ dotsb.}$

Mer presist er dette funksjonen f som er lik mellom og og mellom og for hvert heltall n ; dermed har denne firkantbølgen en hoppdiskontinuitet av høyde ved hvert heltall multiplum av . ${\ displaystyle \ pi /4}$${\ displaystyle 2n \ pi}$${\ displaystyle (2n+1) \ pi}$${\ displaystyle -\ pi /4}$${\ displaystyle (2n+1) \ pi}$${\ displaystyle (2n+2) \ pi}$ ${\ displaystyle \ pi /2}$${\ displaystyle \ pi}$

Som det kan sees, når antall termer stiger, reduseres tilnærmingsfeilen i bredde og energi, men konvergerer til en fast høyde. En beregning for firkantbølgen (se Zygmund, kap. 8.5., Eller beregningene på slutten av denne artikkelen) gir en eksplisitt formel for grensen for feilens høyde. Det viser seg at Fourier -serien overskrider høyden på firkantbølgen med ${\ displaystyle \ pi /4}$

${\ displaystyle {\ frac {1} {2}} \ int _ {0}^{\ pi} {\ frac {\ sin t} {t}} \, dt-{\ frac {\ pi} {4} } = {\ frac {\ pi} {2}} \ cdot (0.089489872236 \ dots)}$( OEIS :  A243268 )

eller omtrent 9 prosent av hoppet. Mer generelt på ethvert hoppe punktet for en stykkevis kontinuerlig differentiable funksjon med et hopp på en , den n- te delvis Fourier-rekker vil (for n stor) oversving denne hoppe ved omtrent i den ene enden og underskridelse det ved den samme grad på den andre slutt; dermed vil "hoppet" i den delvise Fourier -serien være omtrent 18% større enn hoppet i den opprinnelige funksjonen. På stedet for selve diskontinuiteten vil den delvise Fourier -serien konvergere til midtpunktet av hoppet (uavhengig av hva den faktiske verdien av den opprinnelige funksjonen er på dette tidspunktet). Kvantiteten ${\ displaystyle a \ cdot (0.089489872236 \ dots)}$

${\ displaystyle \ int _ {0}^{\ pi} {\ frac {\ sin t} {t}} \ dt = (1.851937051982 \ dots) = {\ frac {\ pi} {2}}+\ pi \ cdot (0.089489872236 \ dots)}$( OEIS :  A036792 )

er noen ganger kjent som Wilbraham - Gibbs -konstanten .

Historie

Gibbs -fenomenet ble først lagt merke til og analysert av Henry Wilbraham i et papir fra 1848. Avisen vakte liten oppmerksomhet til 1914 da den ble nevnt i Heinrich Burkhardts anmeldelse av matematisk analyse i Kleins leksikon . I 1898 utviklet Albert A. Michelson en enhet som kunne beregne og syntetisere Fourier-serien på nytt. En utbredt myte sier at når Fourier -koeffisientene for en firkantbølge ble lagt inn i maskinen, ville grafen svinge ved diskontinuitetene, og at fordi det var en fysisk enhet som var utsatt for produksjonsfeil, var Michelson overbevist om at overskytingen var forårsaket av feil i maskinen. Faktisk var grafene som ble produsert av maskinen ikke gode nok til å vise Gibbs -fenomenet tydelig, og Michelson har kanskje ikke lagt merke til det, da han ikke nevnte denne effekten i sitt papir ( Michelson & Stratton 1898 ) om maskinen sin eller sine senere brev til naturen . Inspirert av en viss korrespondanse i naturen mellom Michelson og Love om konvergensen mellom Fourier -serien i firkantbølgefunksjonen, publiserte J. Willard Gibbs i 1898 et kort notat der han vurderte det som i dag ville bli kalt en sagtannbølge og påpekte det viktige skillet mellom grensen for grafene for delsummene i Fourier -serien, og grafen for funksjonen som er grensen for disse delsummene. I sin første bokstav klarte Gibbs ikke å legge merke til Gibbs -fenomenet, og grensen som han beskrev for grafene for delsummene var unøyaktig. I 1899 publiserte han en korreksjon der han beskrev overskridelsen på tidspunktet for diskontinuitet ( Nature , 27. april 1899, s. 606). I 1906 ga Maxime Bôcher en detaljert matematisk analyse av overskridelsen, og myntet begrepet "Gibbs -fenomen" og tok begrepet i utbredt bruk.

Etter at eksistensen av Henry Wilbrahams papir ble allment kjent, bemerket Horatio Scott Carslaw i 1925 : "Vi kan fortsatt kalle denne egenskapen til Fouriers serier (og visse andre serier) Gibbs fenomen; men vi må ikke lenger hevde at eiendommen først var oppdaget av Gibbs. "

Forklaring

Uformelt gjenspeiler Gibbs -fenomenet vanskeligheten ved å tilnærme seg en diskontinuerlig funksjon av en endelig serie med kontinuerlige sinus- og cosinusbølger. Det er viktig å legge vekt på ordet endelig fordi selv om hver delsum av Fourier -serien overskrider funksjonen den tilnærmer seg, gjør ikke grensen for delsummene det. Verdien av x hvor maksimal overskridelse er oppnådd, beveger seg nærmere og nærmere diskontinuiteten etter hvert som antallet summerte summer øker, så igjen uformelt, når overskridelsen har passert et bestemt x , er konvergens ved den verdien av x mulig.

Det er ingen motsetning i at overskridelsen konvergerer til et beløp som ikke er null, men grensen for delsummene som ikke har noe overskridelse, fordi plasseringen av overskytingen beveger seg. Vi har punktvis konvergens , men ikke ensartet konvergens . For en stykk C ¹ -funksjon konvergerer Fourier -serien til funksjonen på hvert punkt bortsett fra hoppdiskontinuitetene. Ved selve hoppdiskontinuitetene vil grensen konvergere til gjennomsnittet av verdiene til funksjonen på hver side av hoppet. Dette er en konsekvens av Dirichlet -setningen .

Gibbs -fenomenet er også nært knyttet til prinsippet om at forfallet til Fourier -koeffisientene til en funksjon i det uendelige styres av funksjonens jevnhet; veldig jevne funksjoner vil ha veldig raskt nedbrytende Fourier -koeffisienter (noe som resulterer i hurtig konvergens av Fourier -serien), mens diskontinuerlige funksjoner vil ha veldig sakte forfallende Fourier -koeffisienter (noe som får Fourier -serien til å konvergere veldig sakte). Legg for eksempel merke til at Fourier -koeffisientene 1, −1/3, 1/5, ... av den diskontinuerlige firkantbølgen som er beskrevet ovenfor, forfaller bare like raskt som den harmoniske serien , som ikke er helt konvergent ; Faktisk viser den ovennevnte Fourier -serien seg å være bare betinget konvergent for nesten hver verdi av  x . Dette gir en delvis forklaring på Gibbs-fenomenet, siden Fourier-serier med absolutt konvergente Fourier-koeffisienter ville være jevnt konvergente av Weierstrass M-testen og dermed ikke kunne vise den oscillerende atferden ovenfor. På samme måte er det umulig for en diskontinuerlig funksjon å ha absolutt konvergerende Fourier -koeffisienter, siden funksjonen dermed ville være den ensartede grensen for kontinuerlige funksjoner og derfor være kontinuerlig, en motsetning. Se Convergence of Fourier -serien § Absolutt konvergens .

Løsninger

I praksis kan vanskene knyttet til Gibbs-fenomenet forbedres ved å bruke en jevnere metode for Fourierserie summering, for eksempel Fejér summering eller Riesz summering , eller ved å bruke sigma-tilnærming . Ved å bruke en kontinuerlig wavelet -transformasjon, overgår wavelet Gibbs -fenomenet aldri Fourier Gibbs -fenomenet. Ved bruk av den diskrete wavelet -transformasjonen med Haar -grunnfunksjoner forekommer Gibbs -fenomenet ikke i det hele tatt ved kontinuerlige data ved hoppdiskontinuiteter, og er minimalt i det diskrete tilfellet ved store endringspunkter. I wavelet -analyse blir dette ofte referert til som Longo -fenomenet . I polynominterpolasjonsinnstillingen kan Gibbs-fenomenet dempes ved hjelp av S-Gibbs-algoritmen.

Formell matematisk beskrivelse av fenomenet

La oss være en stykkevis kontinuerlig differensierbar funksjon som er periodisk med en periode . Anta at på et tidspunkt varierer venstre og høyre grense for funksjonen med et gap som ikke er null : ${\ displaystyle f: {\ mathbb {R}} \ to {\ mathbb {R}}}$${\ displaystyle L> 0}$${\ displaystyle x_ {0}}$${\ displaystyle f (x_ {0}^{-})}$${\ displaystyle f (x_ {0}^{+})}$${\ displaystyle f}$${\ displaystyle a}$

${\ displaystyle f (x_ {0}^{+})-f (x_ {0}^{-}) = a \ neq 0.}$

For hvert positivt heltall N ≥ 1, la S _N  f være den n. Delvise Fourier -serien

${\ displaystyle S_ {N} f (x): = \ sum _ {-N \ leq n \ leq N} {\ widehat {f}} (n) e^{\ frac {2i \ pi nx} {L} } = {\ frac {1} {2}} a_ {0}+\ sum _ {n = 1}^{N} \ venstre (a_ {n} \ cos \ venstre ({\ frac {2 \ pi nx} {L}} \ høyre)+b_ {n} \ sin \ venstre ({\ frac {2 \ pi nx} {L}} \ høyre) \ høyre),}$

hvor Fourier -koeffisientene er gitt med de vanlige formlene ${\ displaystyle {\ widehat {f}} (n), a_ {n}, b_ {n}}$

${\ displaystyle {\ widehat {f}} (n): = {\ frac {1} {L}} \ int _ {0}^{L} f (x) e^{-2i \ pi nx/L} \, dx}$

${\ displaystyle a_ {n}: = {\ frac {2} {L}} \ int _ {0}^{L} f (x) \ cos \ left ({\ frac {2 \ pi nx} {L} } \ høyre) \, dx}$

${\ displaystyle b_ {n}: = {\ frac {2} {L}} \ int _ {0}^{L} f (x) \ sin \ left ({\ frac {2 \ pi nx} {L} } \ høyre) \, dx.}$

Så har vi

${\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ venstre (x_ {0}+{\ frac {L} {2N}} \ høyre) = f (x_ {0}^{+} )+a \ cdot (0.089489872236 \ dots)}$

og

${\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ venstre (x_ {0}-{\ frac {L} {2N}} \ høyre) = f (x_ {0}^{-} ) -a \ cdot (0.089489872236 \ dots)}$

men

${\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f (x_ {0}) = {\ frac {f (x_ {0}^{-})+f (x_ {0}^{+ })} {2}}.}$

Mer generelt, hvis er en sekvens av reelle tall som konvergerer til som , og hvis gapet a er positivt da ${\ displaystyle x_ {N}}$${\ displaystyle x_ {0}}$${\ displaystyle N \ to \ infty}$

${\ displaystyle \ limsup _ {N \ to \ infty} S_ {N} f (x_ {N}) \ leq f (x_ {0}^{+})+a \ cdot (0.089489872236 \ dots)}$

og

${\ displaystyle \ liminf _ {N \ to \ infty} S_ {N} f (x_ {N}) \ geq f (x_ {0}^{-})-a \ cdot (0.089489872236 \ dots).}$

Hvis gapet a i stedet er negativt, må man bytte grense overordnet med lavere grense , og også bytte ≤ og ≥ tegnene i de to ulikhetene ovenfor.

Forklaring av signalbehandling

Den sinc-funksjonen , den impulsresponsen til et ideelt lavpassfilter . Skalering begrenser funksjonen, og øker tilsvarende størrelsen (som ikke er vist her), men reduserer ikke størrelsen på underslaget, som er integralen i halen.

Fra et signalbehandlingssynspunkt er Gibbs-fenomenet trinnresponsen til et lavpassfilter , og svingningene kalles for ringende eller ringende artefakter . Avkorting av Fourier-transformasjonen av et signal på den virkelige linjen, eller Fourier-serien av et periodisk signal (tilsvarende et signal på sirkelen) tilsvarer å filtrere ut de høyere frekvensene med et ideelt ( murvegg ) lavpass/høy- kutte filter. Dette kan representeres som konvolusjon av det originale signalet med impulsresponsen til filteret (også kjent som kjernen ), som er sinc -funksjonen . Dermed kan Gibbs -fenomenet sees på som et resultat av å ha en Heaviside -trinnfunksjon (hvis periodisitet ikke er nødvendig) eller en firkantbølge (hvis periodisk) med en sinc -funksjon: svingningene i sinc -funksjonen forårsaker krusninger i utgangen.

Den sinus integral , som viser Gibbs-fenomenet for en trinnfunksjon på den virkelige linje.

I tilfelle av å involvere seg med en Heaviside -trinnfunksjon, er den resulterende funksjonen nøyaktig integralen til sinc -funksjonen, sinusintegralen ; for en firkantbølge er beskrivelsen ikke så enkelt sagt. For trinnfunksjonen er størrelsen på underslaget dermed nøyaktig integralen til den (venstre) halen, integrert med det første negative nullet: for normalisert synk av enhetsprøveperiode, er dette Overskytingen er derfor av samme størrelse: integral av høyre hale, eller, som utgjør det samme, forskjellen mellom integralet fra negativ uendelig til det første positive null, minus 1 (verdien for ikke-overskridelse). ${\ displaystyle \ int _ {-\ infty}^{-1} {\ frac {\ sin (\ pi x)} {\ pi x}} \, dx.}$

Overshoot og undershoot kan forstås slik: kjerner normaliseres vanligvis for å ha integral 1, så de resulterer i en kartlegging av konstante funksjoner til konstante funksjoner - ellers har de gevinst . Verdien av en konvolusjon på et punkt er en lineær kombinasjon av inngangssignalet, med koeffisienter (vekter) verdiene til kjernen. Hvis en kjerne er ikke-negativ, for eksempel for en gaussisk kjerne , vil verdien av det filtrerte signalet være en konveks kombinasjon av inngangsverdiene (koeffisientene (kjernen) integreres til 1, og er ikke-negative), og vil dermed falle mellom minimum og maksimum for inngangssignalet - det vil ikke overskride eller overskride. Hvis derimot kjernen antar negative verdier, for eksempel sinc -funksjonen, vil verdien av det filtrerte signalet i stedet være en affin kombinasjon av inngangsverdiene, og kan falle utenfor minimum og maksimum for inngangssignalet , noe som resulterer i undershoot og overshoot, som i Gibbs -fenomenet.

Å ta en lengre ekspansjon-kutte med en høyere frekvens-tilsvarer i frekvensdomenet å utvide murveggen, som i tidsdomenet tilsvarer innsnevring av synkfunksjonen og økning av høyden med den samme faktoren, slik at integralene mellom tilsvarende punkter forblir uendret . Dette er et generelt trekk ved Fourier -transformasjonen: utvidelse i det ene domenet tilsvarer innsnevring og økende høyde i det andre. Dette resulterer i at svingningene i sinc er smalere og høyere og, i den filtrerte funksjon (etter foldings), utbytter svingninger som er smalere og har således mindre område, men ikke reduserer størrelsen: avkutting ved enhver endelige frekvens resulterer i en sinc funksjon, men smal, med de samme halen integraler. Dette forklarer utholdenheten til overskyting og undersving.

• 

  Oscillasjoner kan tolkes som konvolusjon med en sinc.

• 

  Høyere cutoff gjør sinc smalere, men høyere, med samme størrelse halen integraler, gir høyere frekvens svingninger, men hvis størrelse ikke forsvinner.

Således tolkes trekkene ved Gibbs -fenomenet som følger:

• underslaget skyldes at impulsresponsen har et negativt haleintegral, noe som er mulig fordi funksjonen tar negative verdier;
• overskridelsen kompenserer dette ved symmetri (det generelle integralet endres ikke under filtrering);
• oscillasjoners utholdenhet er fordi å øke cutoff reduserer impulsresponsen, men ikke reduserer integralen - oscillasjonene beveger seg dermed mot diskontinuiteten, men reduseres ikke i størrelse.

Eksemplet på firkantbølgen

Animasjon av additiv syntese av en firkantbølge med et økende antall harmoniske. Gibbs -fenomenet er synlig spesielt når antallet harmoniske er stort.

Uten tap av generalitet kan vi anta kvadratbølgetilfellet der perioden L er , diskontinuiteten er på null, og hoppet er lik . For enkelhets skyld, la oss bare behandle saken når N er jevn (tilfellet med oddetall N er veldig likt). Så har vi ${\ displaystyle 2 \ pi}$${\ displaystyle x_ {0}}$${\ displaystyle \ pi /2}$

${\ displaystyle S_ {N} f (x) = \ sin (x)+{\ frac {1} {3}} \ sin (3x)+\ cdots+{\ frac {1} {N-1}} \ synd ((N-1) x).}$

Erstatte , får vi ${\ displaystyle x = 0}$

${\ displaystyle S_ {N} f (0) = 0 = {\ frac {-{\ frac {\ pi} {4}}+{\ frac {\ pi} {4}}} {2}} = {\ frac {f (0^{-})+f (0^{+})} {2}}}$

som hevdet ovenfor. Deretter beregner vi

${\ displaystyle S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = \ sin \ left ({\ frac {\ pi} {N}} \ right)+{\ frac {1} {3}} \ sin \ venstre ({\ frac {3 \ pi} {N}} \ høyre) +\ cdots +{\ frac {1} {N-1}} \ sin \ venstre ({\ frac {(N-1) \ pi} {N}} \ høyre).}$

Hvis vi introduserer den normaliserte sinc -funksjonen , kan vi omskrive dette som ${\ displaystyle \ operatorname {sinc} (x) \,}$

${\ displaystyle S_ {N} f \ left ({\ frac {2 \ pi} {2N}} \ right) = {\ frac {\ pi} {2}} \ left [{\ frac {2} {N} } \ operatorname {sinc} \ left ({\ frac {1} {N}} \ right)+{\ frac {2} {N}} \ operatorname {sinc} \ left ({\ frac {3} {N} } \ right) +\ cdots +{\ frac {2} {N}} \ operatorname {sinc} \ left ({\ frac {(N-1)} {N}} \ right) \ right].}$

Men uttrykket i firkantede parenteser er en Riemann -sum tilnærming til integralet (mer presist, det er en midtpunktsregel tilnærming med mellomrom ). Siden sinc -funksjonen er kontinuerlig, konvergerer denne tilnærmingen til det faktiske integralet som . Slik har vi ${\ displaystyle \ int _ {0}^{1} \ operatorname {sinc} (x) \ dx}$${\ displaystyle 2/N}$${\ displaystyle N \ to \ infty}$

${\ displaystyle {\ begynne {justert} \ lim _ {N \ til \ infty} S_ {N} f \ venstre ({\ frac {2 \ pi} {2N}} \ høyre) & = {\ frac {\ pi } {2}} \ int _ {0}^{1} \ operatorname {sinc} (x) \, dx \\ [8pt] & = {\ frac {1} {2}} \ int _ {x = 0 }^{1} {\ frac {\ sin (\ pi x)} {\ pi x}} \, d (\ pi x) \\ [8pt] & = {\ frac {1} {2}} \ int _ {0}^{\ pi} {\ frac {\ sin (t)} {t}} \ dt \ quad = \ quad {\ frac {\ pi} {4}}+{\ frac {\ pi} { 2}} \ cdot (0.089489872236 \ dots), \ ende {justert}}}$

som var det som ble hevdet i forrige seksjon. En lignende beregning viser

${\ displaystyle \ lim _ {N \ to \ infty} S_ {N} f \ left (-{\ frac {2 \ pi} {2N}} \ right) =-{\ frac {\ pi} {2}} \ int _ {0}^{1} \ operatorname {sinc} (x) \ dx =-{\ frac {\ pi} {4}}-{\ frac {\ pi} {2}} \ cdot (0.089489872236 \ prikker).}$

Konsekvenser

I signalbehandling er Gibbs -fenomenet uønsket fordi det forårsaker artefakter, nemlig klipping fra overskyting og underslag, og ringeartefakter fra svingningene. Ved lavpassfiltrering kan disse reduseres eller elimineres ved å bruke forskjellige lavpassfiltre.

Ved MR forårsaker Gibbs -fenomenet artefakter i nærvær av tilstøtende områder med markant forskjellig signalintensitet. Dette er vanligst ved MR -avbildning i ryggraden, der Gibbs -fenomenet kan simulere utseendet til syringomyelia .

Gibbs -fenomenet manifesterer seg som en kryssmønsterartefakt i den diskrete Fourier -transformasjonen av et bilde, hvor de fleste bilder (f.eks. Mikrografer eller fotografier) ​​har en skarp diskontinuitet mellom grenser øverst / nederst og til venstre / høyre for et bilde. Når periodiske grensebetingelser pålegges i Fourier -transformasjonen, representeres denne hoppdiskontinuiteten ved kontinuitet av frekvenser langs aksene i det gjensidige rommet (dvs. et kryssmønster av intensitet i Fourier -transformasjonen).

Se også

• σ-tilnærming som justerer en Fourier-summering for å eliminere Gibbs-fenomenet som ellers ville oppstå ved diskontinuiteter
• Pinsky -fenomen
• Runges fenomen (et lignende fenomen i polynomtilnærminger)
• Sinus integrert
• Mach band

Merknader

Referanser

• Gibbs, J. Willard (1898), "Fouriers serie" , Nature , 59 (1522): 200, doi : 10.1038/059200b0 , ISSN  0028-0836 , S2CID  4004787
• Gibbs, J. Willard (1899), "Fouriers serie", Nature , 59 (1539): 606, doi : 10.1038/059606a0 , ISSN  0028-0836 , S2CID  13420929
• Michelson, AA; Stratton, SW (1898), "En ny harmonisk analysator", Philosophical Magazine , 5 (45): 85–91
• Antoni Zygmund , Trigonometrical Series , Dover -publikasjoner, 1955.
• Wilbraham, Henry (1848), "On a bestemt periodic function" , The Cambridge and Dublin Mathematical Journal , 3 : 198–201
• Paul J. Nahin , Dr. Eulers Fabulous Formula, Princeton University Press, 2006. Ch. 4, sekt. 4.
• Vretblad, Anders (2000), Fourier Analysis and its Applications , Graduate Texts in Mathematics, 223 , New York: Springer Publishing , s. 93, ISBN 978-0-387-00836-3

Eksterne linker

• Media relatert til Gibbs -fenomenet på Wikimedia Commons
• "Gibbs -fenomen" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Weisstein, Eric W., " Gibbs Phenomenon ". Fra MathWorld - En Wolfram nettressurs.
• Prandoni, Paolo, " Gibbs Phenomenon ".
• Radaelli-Sanchez, Ricardo og Richard Baraniuk, " Gibbs Phenomenon ". The Connexions Project. (Creative Commons Attribution License)
• Horatio S Carslaw: Introduction to the theory of Fouriers series and integrals.pdf (introduksjontot00unkngoog.pdf) på archive.org
• En Python- implementering av S-Gibbs-algoritmen som reduserer Gibbs-fenomenet https://github.com/pog87/FakeNodes .