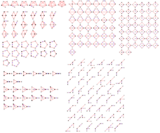Coxeter - Dynkin -diagram - Coxeter–Dynkin diagram
I geometri er et Coxeter - Dynkin -diagram (eller Coxeter -diagram , Coxeter -graf ) en graf med numerisk merkede kanter (kalt grener ) som representerer de romlige forholdene mellom en samling speil (eller reflekterende hyperplan ). Den beskriver en allsidig konstruksjon: hver graf "node" representerer et speil (domene fasett ), og merket som er festet til en gren koder for den to-plans vinkelen rekkefølgen mellom to speil (på en domene ridge ), det vil si den mengde ved hvilken vinkelen mellom reflekterende fly kan multipliseres med for å få 180 grader. En umerket gren representerer implisitt ordre-3 (60 grader).
Hvert diagram representerer en Coxeter -gruppe , og Coxeter -grupper er klassifisert etter tilhørende diagrammer.
Dynkin -diagrammer er nært beslektede objekter, som skiller seg fra Coxeter -diagrammer i to henseender: For det første rettes grener merket med "4" eller høyere , mens Coxeter -diagrammer er uorienterte ; for det andre må Dynkin -diagrammer tilfredsstille en ytterligere ( krystallografisk ) begrensning, nemlig at de eneste tillatte grenetikettene er 2, 3, 4 og 6. Dynkin -diagrammer tilsvarer og brukes til å klassifisere rotsystemer og derfor semi -enkle Lie -algebraer .
Beskrivelse
Grener av et Coxeter - Dynkin -diagram er merket med et rasjonelt tall p , som representerer en dihedral vinkel på 180 °/ p . Når p = 2 er vinkelen 90 ° og speilene ikke har noen interaksjon, så grenen kan utelates fra diagrammet. Hvis en gren er umerket, antas den å ha p = 3 , som representerer en vinkel på 60 °. To parallelle speil har en gren merket med "∞". I prinsippet kan n speil representeres av en komplett graf der alle n ( n - 1) / 2 grener er tegnet. I praksis inkluderer nesten alle interessante konfigurasjoner av speil et antall rette vinkler, så de tilsvarende grenene utelates.
Diagrammer kan merkes med grafstrukturen. De første formene studert av Ludwig Schläfli er ortoskjemaene som har lineære grafer som genererer vanlige polytoper og vanlige honningkaker . Plagioskjemaer er forenklinger representert ved forgreningsgrafer, og sykloskjemaer er forenklinger representert med sykliske grafer.
Schläfli matrise
Hvert Coxeter -diagram har en tilsvarende Schläfli -matrise (så oppkalt etter Ludwig Schläfli ), med matriseelementer a i, j = a j, i = −2cos ( π / p ) hvor p er grenrekkefølgen mellom speilparene . Som en matrise av cosinus kalles den også en Gramian -matrise etter Jørgen Pedersen Gram . Alle Coxeter -gruppen Schläfli -matriser er symmetriske fordi rotvektorene deres er normaliserte. Det er nært knyttet til Cartan -matrisen , brukt i de lignende, men rettet graf Dynkin -diagrammer i de begrensede tilfellene p = 2,3,4 og 6, som IKKE er symmetriske generelt.
Determinanten for Schläfli -matrisen, kalt Schläflian , og dens tegn avgjør om gruppen er endelig (positiv), affin (null), ubestemt (negativ). Denne regelen kalles Schläflis kriterium .
De egenverdiene av Schläfli matrisen avgjør hvorvidt en Coxeter gruppe er av endelig typen (alle positive), affine typen (alle ikke-negativ, i det minste ett er null), eller ubestemt typen (annet). Den ubestemte typen er noen ganger ytterligere delt inn, f.eks. I hyperboliske grupper og andre Coxeter -grupper. Imidlertid er det flere ikke-ekvivalente definisjoner for hyperbolske Coxeter-grupper. Vi bruker følgende definisjon: En Coxeter -gruppe med tilkoblet diagram er hyperbolsk hvis den verken er av endelig eller affin type, men hvert riktig tilkoblet underdiagram er av endelig eller affin type. En hyperbolsk Coxeter -gruppe er kompakt hvis alle undergrupper er begrensede (dvs. har positive determinanter), og parakompakterer hvis alle dens undergrupper er endelige eller affine (dvs. har ikke -negative determinanter).
Endelige og affine grupper kalles også henholdsvis elliptiske og parabolske . Hyperboliske grupper kalles også Lannér, etter F. Lannér som regnet de kompakte hyperbolske gruppene i 1950, og Koszul (eller kvasi-Lannér) for parakompaktgruppene.
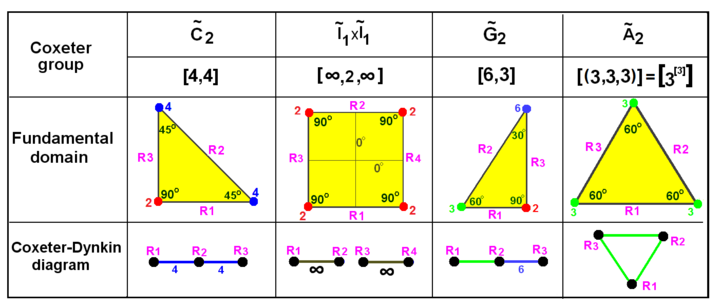
Rang 2 Coxeter -grupper
For rang 2 bestemmes typen av en Coxeter -gruppe fullt ut av determinanten til Schläfli -matrisen, ettersom den ganske enkelt er produktet av egenverdiene: Endelig type (positiv determinant), affin type (null determinant) eller hyperbolisk (negativ determinant) . Coxeter bruker en tilsvarende brakettnotasjon som viser sekvenser av grenordrer som en erstatning for node-branch grafiske diagrammer. Rasjonelle løsninger [p/q],![]()
![]()
![]()
![]()
![]() finnes også, med gcd (p, q) = 1, som definerer overlappende grunnleggende domener. For eksempel 3/2, 4/3, 5/2, 5/3, 5/4. og 6/5.
finnes også, med gcd (p, q) = 1, som definerer overlappende grunnleggende domener. For eksempel 3/2, 4/3, 5/2, 5/3, 5/4. og 6/5.
| Type | Avgrenset | Affine | Hyperbolsk | |||||
|---|---|---|---|---|---|---|---|---|
| Geometri |

|

|

|

|
... |

|

|

|
| Coxeter |
[] |
[2] |
[3] |
[4] |
[p] |
[∞] |
[∞] |
[iπ/λ] |
| Rekkefølge | 2 | 4 | 6 | 8 | 2 s | ∞ | ||
| Speillinjer er farget for å tilsvare Coxeter -diagramnoder. Grunnleggende domener er vekselvis farget. |
||||||||
| Rang 2 Coxeter -gruppediagrammer | |||||||
|---|---|---|---|---|---|---|---|
|
Bestill s |
Gruppe | Coxeter diagram | Schläfli matrise | ||||
| Determinant (4-a 21 *a 12 ) |
|||||||
| Endelig (determinant> 0) | |||||||
| 2 | I 2 (2) = A 1 xA 1 | [2] | 4 | ||||
| 3 | I 2 (3) = A 2 | [3] | 3 | ||||
| 3/2 | [3/2] | ||||||
| 4 | I 2 (4) = B 2 | [4] | 2 | ||||
| 4/3 | [4/3] | ||||||
| 5 | I 2 (5) = H 2 | [5] |
~ 1.38196601125 |
||||
| 5/4 | [5/4] | ||||||
| 5/2 | [5/2] |
~ 3.61803398875 |
|||||
| 5/3 | [5/3] | ||||||
| 6 | I 2 (6) = G 2 | [6] | 1 | ||||
| 6/5 | [6/5] | ||||||
| 8 | I 2 (8) | [8] |
~ 0,58578643763 |
||||
| 10 | I 2 (10) | [10] |
~ 0.38196601125 |
||||
| 12 | I 2 (12) | [12] |
~ 0.26794919243 |
||||
| s | I 2 (p) | [p] | |||||
| Affine (Determinant = 0) | |||||||
| ∞ | I 2 (∞) = = | [∞] | 0 | ||||
| Hyperbolisk (Determinant≤0) | |||||||
| ∞ | [∞] | 0 | |||||
| ∞ | [iπ/λ] | ||||||
Geometriske visualiseringer
Coxeter - Dynkin -diagrammet kan sees på som en grafisk beskrivelse av speilets grunnleggende domene . Et speil representerer et hyperplan innenfor et gitt dimensjonalt sfærisk eller euklidisk eller hyperbolsk rom. (I 2D -mellomrom er et speil en linje, og i 3D er et speil et fly).
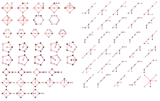
Disse visualiseringene viser de grunnleggende domenene for 2D- og 3D -euklidiske grupper og 2D -sfæriske grupper. For hver kan Coxeter-diagrammet utledes ved å identifisere hyperplan-speilene og merke tilkoblingen, ignorere 90-graders dihedrale vinkler (rekkefølge 2).
 Coxeter -grupper i det euklidiske planet med likeverdige diagrammer. Refleksjoner er merket som grafnoder R 1, R2 , etc. og er farget av deres refleksjonsrekkefølge. Refleksjoner ved 90 grader er inaktive og undertrykkes derfor fra diagrammet. Parallelle speil er forbundet med en ∞ merket gren. Den prismatiske gruppen x vises som en dobling av , men kan også opprettes som rektangulære domener fra dobling av trekanter. Det er en dobling av trekanten. |
|
 Mange Coxeter -grupper i det hyperboliske planet kan utvides fra de euklidiske tilfellene som en serie hyperboliske løsninger. |
|
 Coxeter grupper i 3-mellomrom med diagrammer. Speil (trekantflater) er merket med motsatt toppunkt 0..3. Grener er farget av deres refleksjonsrekkefølge. fyller 1/48 av terningen. fyller 1/24 av terningen. fyller 1/12 av terningen. |
 Coxeter -grupper i sfæren med tilsvarende diagrammer. Ett grunnleggende domene er skissert med gult. Domenekropper (og grafgreiner) er farget av deres refleksjonsrekkefølge. |
Endelige Coxeter -grupper
- Se også polytopfamilier for en tabell med ensartede polytoper med sluttnode assosiert med disse gruppene.
- Tre forskjellige symboler gis for de samme gruppene - som en bokstav/et tall, som et sett med parenteser og som Coxeter -diagrammet.
- De todelt D n -gruppene er halv eller alternativ versjon av de vanlige C n -gruppene.
- De todelt D n og E n gruppene er også merket med en overskrift [3 a , b , c ] hvor a , b , c er antall segmenter i hver av de tre grenene.
| Rang | Simple Lie -grupper | Eksepsjonelle løgngrupper | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | A 1 = [] |
|||||||
| 2 | A 2 = [3] |
B 2 = [4] |
D 2 = A 1 A 1 |
G 2 = [6] |
H 2 = [5] |
I 2 [p] |
||
| 3 | A 3 = [3 2 ] |
B 3 = [3,4] |
D 3 = A 3 |
E 3 = A 2 A 1 |
F 3 = B 3 |
H 3 |
||
| 4 | A 4 = [3 3 ] |
B 4 = [3 2 , 4] |
D 4 = [3 1,1,1 ] |
E 4 = A 4 |
F 4 |
H 4 |
||
| 5 | A 5 = [3 4 ] |
B 5 = [3 3 , 4] |
D 5 = [3 2,1,1 ] |
E 5 = D 5 |
||||
| 6 | A 6 = [3 5 ] |
B 6 = [3 4 , 4] |
D 6 = [3 3,1,1 ] |
E 6 = [3 2,2,1 ] |
||||
| 7 | A 7 = [3 6 ] |
B 7 = [3 5 , 4] |
D 7 = [3 4,1,1 ] |
E 7 = [3 3,2,1 ] |
||||
| 8 | A 8 = [3 7 ] |
B 8 = [3 6 , 4] |
D 8 = [3 5,1,1 ] |
E 8 = [3 4,2,1 ] |
||||
| 9 | A 9 = [3 8 ] |
B 9 = [3 7 , 4] |
D 9 = [3 6,1,1 ] |
|||||
| 10+ | .. | .. | .. | .. | ||||
Påføring med ensartede polytoper
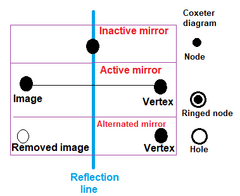 Ved konstruksjon av ensartede polytoper markeres noder som aktive av en ring hvis et generatorpunkt er utenfor speilet, og skaper en ny kant mellom et generatorpunkt og dets speilbilde. En ikke -ringet node representerer et inaktivt speil som ikke genererer nye punkter. En ring uten node kalles et hull . |
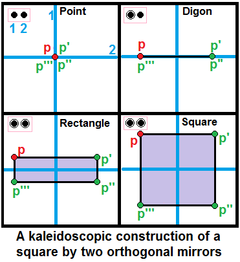 To ortogonale speil kan brukes til å generere et kvadrat, |
Coxeter - Dynkin -diagrammer kan eksplisitt oppregne nesten alle klasser av ensartet polytop og ensartede tessellasjoner . Hver ensartet polytop med ren reflekterende symmetri (alle unntatt noen få spesielle tilfeller har ren refleksjonssymmetri) kan representeres av et Coxeter - Dynkin -diagram med permutasjoner av markeringer . Hver uniform polytopen kan genereres ved anvendelse av slike speil og et enkelt generator Punkt: speilbilder skape nye punkter som refleksjoner, så polytopen kanter kan være definert mellom punktene og en speilbilledpunkt. Ansikter genereres ved gjentatt refleksjon av en kant som til slutt vikles rundt til den opprinnelige generatoren; den endelige formen, så vel som alle høyere dimensjonale fasetter, blir på samme måte skapt av at ansiktet reflekteres for å omslutte et område.
For å spesifisere det genererende toppunktet, er en eller flere noder merket med ringer, noe som betyr at toppunktet ikke er på speilet / speilene som er representert av den / de ringede noden. (Hvis to eller flere speil er merket, er toppunktet like langt fra dem.) Et speil er aktivt (skaper refleksjoner) bare med hensyn til punkter som ikke er på det. Et diagram trenger minst en aktiv node for å representere en polytop. Et ikke-koblet diagram (undergrupper atskilt med ordre-2 grener eller ortogonale speil) krever minst én aktiv node i hver undergraf.
Alle vanlige polytoper , representert med Schläfli -symbolet { p , q , r , ... }, kan få sine grunnleggende domener representert med et sett med n speil med et beslektet Coxeter - Dynkin -diagram over en linje med noder og grener merket med p , q , r , ..., med den første noden ringt.
Uniforme polytoper med en ring tilsvarer generatorpunkter i hjørnene av det grunnleggende domenet simplex. To ringer tilsvarer kantene på simplex og har en grad av frihet, med bare midtpunktet som den ensartede løsningen for like kantlengder. Generelt er k -ringgeneratorpunkter på (k -1 ) -fasene til simplexen, og hvis alle nodene er ringet, er generatorpunktet i det indre av simplexen.
Spesialtilfellet for ensartede polytoper med ikke-reflekterende symmetri er representert ved en sekundær markering der den sentrale prikken i en ringet node er fjernet (kalt et hull ). Disse formene er vekslinger av polytoper med reflekterende symmetri, noe som betyr at hvert annet toppunkt blir slettet. Den resulterende polytopen vil ha en subsymmetri av den opprinnelige Coxeter -gruppen . En avkortet veksling kalles en snub .
- En enkelt node representerer et enkelt speil. Dette kalles gruppe A 1 . Hvis det er ringet, skaper dette et linjestykke vinkelrett på speilet, representert som {}.
- To ufestede noder representerer to vinkelrette speil. Hvis begge noder er ringet, kan det opprettes et rektangel , eller et kvadrat hvis punktet er i lik avstand fra begge speilene.
- To noder festet av en ordre- n gren kan opprette et n -gon hvis punktet er på ett speil, og et 2 n -gon hvis punktet er av begge speilene. Dette danner I 1 (n) -gruppen.
- To parallelle speil kan representere en uendelig polygon I 1 (∞) gruppe, også kalt Ĩ 1 .
- Tre speil i en trekant danner bilder sett i et tradisjonelt kalejdoskop og kan representeres av tre noder forbundet i en trekant. Gjentatte eksempler vil ha grener merket som (3 3 3), (2 4 4), (2 3 6), selv om de to siste kan tegnes som en linje (med de 2 grenene ignorert). Disse vil generere ensartede fliser .
- Tre speil kan generere ensartede polyeder ; inkludert rasjonelle tall gir settet med Schwarz -trekanter .
- Tre speil med ett vinkelrett på de to andre kan danne de ensartede prismer .
 Det er 7 reflekterende uniformskonstruksjoner i en generell trekant, basert på 7 topologiske generatorposisjoner innenfor det grunnleggende domenet. Hvert aktivt speil genererer en kant, med to aktive speil har generatorer på domenesidene og tre aktive speil har generatoren i interiøret. En eller to frihetsgrader kan løses for en unik posisjon for like kantlengder på det resulterende polyeder eller flislegging. |
 Eksempel 7 generatorer på oktaedrisk symmetri , grunnleggende trekant (4 3 2), med åttende snubgenerasjon som alternativ |
Dualene til de ensartede polytopene er noen ganger merket med en vinkelrett skråstrekning som erstatter ringede noder, og et skråhull for hullnoder i snubbene. For eksempel,![]()
![]()
![]() representerer et rektangel (som to aktive ortogonale speil), og
representerer et rektangel (som to aktive ortogonale speil), og![]()
![]()
![]() representerer dens doble polygon , romben .
representerer dens doble polygon , romben .
Eksempel på polyeder og fliser
For eksempel har B 3 Coxeter -gruppen et diagram:![]()
![]()
![]()
![]()
![]() . Dette kalles også oktaedrisk symmetri .
. Dette kalles også oktaedrisk symmetri .
Det er 7 konvekse, ensartede polyeder som kan konstrueres fra denne symmetri -gruppen og 3 fra vekslende undersymmetrier, hver med et unikt merket Coxeter - Dynkin -diagram. Den Wythoff symbol representerer et spesialtilfelle av den Coxeter diagrammet for rang 3 grafer, med alle 3 gren ordrer heter, snarere enn å undertrykke den orden 2 grener. Wythoff -symbolet er i stand til å håndtere snubformen , men ikke generelle vekslinger uten at alle noder er ringet.
| Uniform oktaedrisk polyeder | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri : [4,3], (*432) | [4,3] + (432) |
[1 + , 4,3] = [3,3] (*332) |
[3 + , 4] (3*2) |
|||||||
| {4,3} | t {4,3} |
r {4,3} r {3 1,1 } |
t {3,4} t {3 1,1 } |
{3,4} {3 1,1 } |
rr {4,3} s 2 {3,4} |
tr {4,3} | sr {4,3} |
h {4,3} {3,3} |
h 2 {4,3} t {3,3} |
s {3,4} s {3 1,1 } |
|
|
|
|
|
|
|
|
|
|
||
|
= |
= |
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
| Dualer til ensartet polyeder | ||||||||||
| V4 3 | V3.8 2 | V (3.4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | V3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
De samme konstruksjoner kan gjøres på usammenhengende (ortogonale) Coxeter grupper som de ensartede prismer , og kan sees mer tydelig som tilings av dihedrons og hosohedrons på kulen, slik [6] x [] eller [6,2] familie:
| Uniform sekskantet dihedral sfærisk polyeder | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri : [6,2] , (*622) | [6,2] + , (622) | [6,2 + ], (2*3) | ||||||||||||

|
|

|

|

|
|

|

|

|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
| {6,2} | t {6,2} | r {6,2} | t {2,6} | {2,6} | rr {6,2} | tr {6,2} | sr {6,2} | s {2,6} | ||||||
| Dualer til uniformer | ||||||||||||||

|

|

|

|

|

|

|

|

|
||||||
| V6 2 | V12 2 | V6 2 | V4.4.6 | V2 6 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
Til sammenligning er [6,3], ![]()
![]()
![]()
![]()
![]() familien produserer et parallelt sett med 7 ensartede fliser på det euklidiske planet, og deres doble fliser. Det er igjen 3 alternativer og en halv symmetriversjon.
familien produserer et parallelt sett med 7 ensartede fliser på det euklidiske planet, og deres doble fliser. Det er igjen 3 alternativer og en halv symmetriversjon.
| Ensartede sekskantede/trekantede fliser | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri : [6,3], (*632) | [6,3] + (632) |
[6,3 + ] (3*3) |
|||||||||
| {6,3} | t {6,3} | r {6,3} | t {3,6} | {3,6} | rr {6,3} | tr {6,3} | sr {6,3} | s {3,6} | |||
|
|
|
|
|
|
|
|
|
|
|||

|

|

|

|

|

|

|

|

|
|||
| 6 3 | 3.12 2 | (3.6) 2 | 6.6.6 | 3 6 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Ensartede dueller | |||||||||||

|

|

|

|

|

|

|

|

|
|||
| V6 3 | V3.12 2 | V (3.6) 2 | V6 3 | V3 6 | V3.4.6.4 | V.4.6.12 | V3 4 .6 | V3 6 | |||
I det hyperboliske planet [7,3], ![]()
![]()
![]()
![]()
![]() familien produserer et parallelt sett med ensartede fliser, og deres dobbelte fliser. Det er bare 1 veksling ( snub ) siden alle grenordre er merkelige. Mange andre hyperbolske familier med ensartede fliser kan sees ved ensartede fliser i hyperbolsk plan .
familien produserer et parallelt sett med ensartede fliser, og deres dobbelte fliser. Det er bare 1 veksling ( snub ) siden alle grenordre er merkelige. Mange andre hyperbolske familier med ensartede fliser kan sees ved ensartede fliser i hyperbolsk plan .
| Ensartede heptagonale/trekantede fliser | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri: [7,3], (*732) | [7,3] + , (732) | ||||||||||
|
|
|
|
|
|
|
|
|
||||

|

|

|

|

|

|

|

|
||||
| {7,3} | t {7,3} | r {7,3} | t {3,7} | {3,7} | rr {7,3} | tr {7,3} | sr {7,3} | ||||
| Ensartede dueller | |||||||||||
|
|
|
|
|
|
|
|
|
||||

|

|

|

|

|

|

|

|
||||
| V7 3 | V3.14.14 | V3.7.3.7 | V6.6.7 | V3 7 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
Affinere Coxeter -grupper
Familier med konvekse uniforme euklidiske tessellasjoner er definert av de affine Coxeter -gruppene . Disse gruppene er identiske med de endelige gruppene med inkludering av en ekstra node. I bokstavnavn får de den samme bokstaven med et "~" over bokstaven. Indeksen refererer til den endelige gruppen, så rangen er indeksen pluss 1. ( Ernst Witt -symboler for affinegruppene er gitt som også )
- : diagrammer av denne typen er sykluser. (Også P n )
- er knyttet til hyperkuben vanlig tessellasjon { 4, 3, ...., 4 } familie. (Også R n )
- relatert til C med ett fjernet speil. (Også S n )
- relatert til C med to fjernede speil. (Også Q n )
- , , . (Også T 7 , T 8 , T 9 )
- danner den {3,4,3,3} vanlige tessellasjonen. (Også U 5 )
- danner 30-60-90 trekantfundamentale domener. (Også V 3 )
- er to parallelle speil. (= = ) (Også W 2 )
Sammensatte grupper kan også defineres som ortogonale prosjekter. Den vanligste bruken , som ,![]()
![]()
![]()
![]()
![]()
![]()
![]() representerer firkantede eller rektangulære sjakkbrettdomener i det euklidiske planet. Og
representerer firkantede eller rektangulære sjakkbrettdomener i det euklidiske planet. Og ![]()
![]()
![]()
![]()
![]()
![]()
![]() representerer trekantede prismer grunnleggende domener i euklidisk 3-rom.
representerer trekantede prismer grunnleggende domener i euklidisk 3-rom.
| Rang | (P 2+ ) | (S 4+ ) | (R 2+ ) | (Q 5+ ) | (T n+1 ) / (U 5 ) / (V 3 ) |
|---|---|---|---|---|---|
| 2 |
= [∞] |
= [∞] |
|||
| 3 |
= [3 [3] ] * |
= [4,4] * |
= [6,3] * |
||
| 4 |
= [3 [4] ] * |
= [4,3 1,1 ] * |
= [4,3,4] * |
= [3 1,1 , 3 −1 , 3 1,1 ] |
|
| 5 |
= [3 [5] ] * |
= [4,3,3 1,1 ] * |
= [4,3 2 , 4] * |
= [3 1,1,1,1 ] * |
= [3,4,3,3] * |
| 6 |
= [3 [6] ] * |
= [4,3 2 , 3 1,1 ] * |
= [4,3 3 , 4] * |
= [3 1,1 , 3,3 1,1 ] * |
|
| 7 |
= [3 [7] ] * |
= [4,3 3 , 3 1,1 ] |
= [4,3 4 , 4] |
= [3 1,1 , 3 2 , 3 1,1 ] |
= [3 2,2,2 ] |
| 8 |
= [3 [8] ] * |
= [4,3 4 , 3 1,1 ] * |
= [4,3 5 , 4] |
= [3 1,1 , 3 3 , 3 1,1 ] * |
= [3 3,3,1 ] * |
| 9 |
= [3 [9] ] * |
= [4,3 5 , 3 1,1 ] |
= [4,3 6 , 4] |
= [3 1,1 , 3 4 , 3 1,1 ] |
= [3 5,2,1 ] * |
| 10 |
= [3 [10] ] * |
= [4,3 6 , 3 1,1 ] |
= [4,3 7 , 4] |
= [3 1,1 , 3 5 , 3 1,1 ] |
|
| 11 | ... | ... | ... | ... |
Hyperboliske Coxeter -grupper
Det er mange uendelige hyperbolske Coxeter -grupper . Hyperboliske grupper er kategorisert som kompakte eller ikke, med kompakte grupper som har begrensede grunnleggende domener. Kompakte simplex hyperbolske grupper ( Lannér simplices ) eksisterer som rang 3 til 5. Paracompact simplex grupper ( Koszul simplices ) eksisterer opp til rang 10. Hypercompact ( Vinberg polytoper ) grupper har blitt utforsket, men ikke blitt fullstendig bestemt. I 2006 beviste Allcock at det er uendelig mange kompakte Vinberg-polytoper for dimensjoner opptil 6, og uendelig mange begrensede Vinberg-polytoper for dimensjoner opp til 19, så en fullstendig oppregning er ikke mulig. Alle disse grunnleggende reflekterende domenene, både enkle og ikke -enkle, kalles ofte Coxeter -polytoper eller noen ganger mindre nøyaktig Coxeter -polyeder .
Hyperboliske grupper i H 2
| Eksempel høyre trekanter [p, q] | ||||
|---|---|---|---|---|
 [3,7] |
 [3,8] |
 [3,9] |
 [3, ∞] |
|
 [4,5] |
 [4,6] |
 [4,7] |
 [4,8] |
 [∞, 4] |
 [5,5] |
 [5,6] |
 [5,7] |
 [6,6] |
 [∞, ∞] |
| Eksempel på generelle trekanter [(p, q, r)] | ||||
 [(3,3,4)] |
 [(3,3,5)] |
 [(3,3,6)] |
 [(3,3,7)] |
 [(3,3, ∞)] |
 [(3,4,4)] |
 [(3,6,6)] |
 [(3, ∞, ∞)] |
 [(6,6,6)] |
 [(∞, ∞, ∞)] |
Tredimensjonale hyperbolske trekantgrupper eksisterer som rang 3 koxeterdiagrammer, definert av trekant (pqr) for:
Det er uendelig mange kompakte trekantede hyperbolske Coxeter -grupper, inkludert lineære og trekantede grafer. De lineære grafene finnes for rette trekanter (med r = 2).
| Lineær | Syklisk | ||||
|---|---|---|---|---|---|
|
∞ [p, q], 2 (p+q) <pq
|
∞ [(p, q, r)],
|
Paracompact Coxeter -grupper av rang 3 eksisterer som grenser for de kompakte.
| Lineære grafer | Sykliske grafer |
|---|---|
|
|
Aritmetisk trekantgruppe
De hyperbolske trekantsgruppene som også er aritmetiske grupper, danner en endelig delmengde. Ved datasøk ble den komplette listen bestemt av Kisao Takeuchi i hans aritmetiske trekantgrupper fra 1977 . Det er 85 totalt, 76 kompakte og 9 parakompakte.
| Høyre trekanter (pq 2) | Generelle trekanter (pqr) |
|---|---|
Kompakte grupper: (76)
Parakompakte høyre trekanter: (4)
|
Generelle trekanter: (39)
Parakompakte generelle trekanter: (5)
|
|
|
Hyperboliske koxeterpolygoner over trekanter
Andre H 2 hyperbolske kaleidoskoper kan konstrueres fra høyere ordens polygoner. I likhet med trekantsgrupper kan disse kalejdoskopene identifiseres ved en syklisk sekvens av speilskjæringsordrer rundt det grunnleggende domenet, som (abcd ...), eller tilsvarende i orbifold notasjon som * abcd .... Coxeter - Dynkin -diagrammer for disse polygonale kalejdoskopene kan bli sett på som en degenerert (n-1) -simplex grunnleggende domener, med en syklisk av grener for a, b, c ... og de resterende n*(n-3)/2 grenene er merket som uendelige (∞) som representerer speilene som ikke krysser hverandre. Det eneste nonhyperboliske eksemplet er euklidisk symmetri fire speil i et kvadrat eller rektangel som![]()
![]()
![]()
![]()
![]()
![]()
![]() , [∞, 2, ∞] (orbifold *2222). En annen grenrepresentasjon for ikke-kryssende speil av Vinberg gir uendelige grener som stiplede eller stiplede linjer, så dette diagrammet kan vises som
, [∞, 2, ∞] (orbifold *2222). En annen grenrepresentasjon for ikke-kryssende speil av Vinberg gir uendelige grener som stiplede eller stiplede linjer, så dette diagrammet kan vises som![]()
![]()
![]() , med de fire ordre-2 grenene undertrykt rundt omkretsen.
, med de fire ordre-2 grenene undertrykt rundt omkretsen.
For eksempel vil et firkantet domene (abcd) ha to uendelige rekkefølger som forbinder ultraparallelle speil. Det minste hyperboliske eksemplet er![]()
![]()
![]()
![]()
![]()
![]()
![]() , [∞, 3, ∞] eller [iπ/λ 1 , 3, iπ/λ 2 ] (orbifold *3222), hvor (λ 1 , λ 2 ) er avstanden mellom de ultraparallelle speilene. Det alternative uttrykket er
, [∞, 3, ∞] eller [iπ/λ 1 , 3, iπ/λ 2 ] (orbifold *3222), hvor (λ 1 , λ 2 ) er avstanden mellom de ultraparallelle speilene. Det alternative uttrykket er![]()
![]()
![]() , med tre ordre-2 grener undertrykt rundt omkretsen. På samme måte (2 3 2 3) (orbifold *3232) kan representeres som
, med tre ordre-2 grener undertrykt rundt omkretsen. På samme måte (2 3 2 3) (orbifold *3232) kan representeres som![]()
![]()
![]() og (3 3 3 3), (orbifold *3333) kan representeres som en komplett graf
og (3 3 3 3), (orbifold *3333) kan representeres som en komplett graf ![]()
![]()
![]() .
.
Det høyeste firkantede domenet (∞ ∞ ∞ ∞) er en uendelig firkant, representert av en fullstendig tetraedral graf med 4 omkretsgreiner som ideelle hjørner og to diagonale grener som uendelig (vist som stiplede linjer) for ultraparallelle speil:![]()
![]()
![]()
![]()
![]() .
.
Kompakt (Lannér simplex -grupper)
Kompakte hyperboliske grupper kalles Lannér -grupper etter Folke Lannér som først studerte dem i 1950. De eksisterer bare som rang 4 og 5 grafer. Coxeter studerte de lineære hyperboliske coxeter-gruppene i sitt papir fra 1954 Regular Honeycombs in hyperbolic space , som inkluderte to rasjonelle løsninger i hyperbolsk 4-space : [5/2,5,3,3] =![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() og [5,5/2,5,3] =
og [5,5/2,5,3] = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Rangerer 4–5
Det grunnleggende domenet til en av de to todelende gruppene, [5,3 1,1 ] og [5,3,3 1,1 ], er det dobbelte av en tilsvarende lineær gruppe, [5,3,4] og [5 , 3,3,4]. Brevnavn er gitt av Johnson som utvidede Witt -symboler .
| Dimensjon H d |
Rang | Totalt antall | Lineær | Bifurcating | Syklisk |
|---|---|---|---|---|---|
| H 3 | 4 | 9 |
= [4,3,5]: |
= [5,3 1,1 ]: |
= [(3 3 , 4)]: |
| H 4 | 5 | 5 |
= [3 3 , 5]: |
= [5,3,3 1,1 ]: |
= [(3 4 , 4)]: |
Paracompact (Koszul simplex -grupper)

Paracompact (også kalt noncompact) hyperbolske Coxeter -grupper inneholder affine undergrupper og har asymptotiske simplex grunnleggende domener. Den høyeste parakompakte hyperbolske Coxeter-gruppen er rang 10. Disse gruppene er oppkalt etter den franske matematikeren Jean-Louis Koszul . De kalles også kvasi-Lannér-grupper som utvider de kompakte Lannér-gruppene. Listen ble bestemt fullstendig ved datasøk av M. Chein og publisert i 1969.
Av Vinberg er alle unntatt åtte av disse 72 kompakte og parakompakte forenklingene aritmetiske. To av de ikke -aritmetiske gruppene er kompakte:![]()
![]()
![]()
![]()
![]() og
og ![]()
![]()
![]()
![]()
![]()
![]() . De seks andre ikke-aritmetiske gruppene er alle parakompakte, med fem tredimensjonale grupper
. De seks andre ikke-aritmetiske gruppene er alle parakompakte, med fem tredimensjonale grupper![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() , og
, og ![]()
![]()
![]()
![]()
![]() og en 5-dimensjonal gruppe
og en 5-dimensjonal gruppe ![]()
![]()
![]()
![]()
![]()
![]() .
.
Ideelle forenklinger
Det er 5 hyperbolske Coxeter -grupper som uttrykker ideelle forenklinger , grafer der fjerning av en node resulterer i en affin Coxeter -gruppe. Således er alle hjørner av denne ideelle simplexen i det uendelige.
| Rang | Ideell gruppe | Affinere undergrupper | ||
|---|---|---|---|---|
| 3 | [(∞, ∞, ∞)] |
|
[∞] |
|
| 4 | [4 [4] ] |
|
[4,4] |
|
| 4 | [3 [3,3] ] |
|
[3 [3] ] |
|
| 4 | [(3,6) [2] ] |
|
[3,6] |
|
| 6 | [(3,3,4) [2] ] |
|
[4,3,3,4], [3,4,3,3] |
|
Rangerer 4–10

Det er totalt 58 parakompakte hyperbolske Coxeter -grupper fra rang 4 til 10. Alle 58 er gruppert nedenfor i fem kategorier. Brevsymboler er gitt av Johnson som Extended Witt -symboler , ved å bruke PQRSTWUV fra de affine Witt -symbolene, og legge til LMNOXYZ. Disse hyperboliske gruppene får en overlinje, eller en hatt, for sykloskjemaer. Den brakett notasjon fra Coxeter er et linearisert representasjon av Coxeter gruppe.
| Rang | Totalt antall | Grupper | |||
|---|---|---|---|---|---|
| 4 | 23 |
= [(3,3,4,4)]: |
= [3,3 [3] ]: |
= [3,4,4]: |
= [3 [] x [] ]: |
| 5 | 9 |
= [3,3 [4] ]: |
= [4,3, ((4,2,3))]: |
= [(3,4) 2 ]: |
= [4,3 1,1,1 ]: |
| 6 | 12 |
= [3,3 [5] ]: |
= [4,3,3 2,1 ]: |
= [3 3 , 4,3]: |
= [3 2,1,1,1 ]: = [4,3,3 1,1,1 ]: |
| 7 | 3 |
= [3,3 [6] ]: |
= [3 1,1 , 3,3 2,1 ]: |
= [4,3 2 , 3 2,1 ]: |
|
| 8 | 4 |
= [3,3 [7] ]: |
= [3 1,1 , 3 2 , 3 2,1 ]: |
= [4,3 3 , 3 2,1 ]: |
= [3 3,2,2 ]: |
| 9 | 4 |
= [3,3 [8] ]: |
= [3 1,1 , 3 3 , 3 2,1 ]: |
= [4,3 4 , 3 2,1 ]: |
= [3 4,3,1 ]: |
| 10 | 4 |
= [3,3 [9] ]: |
= [3 1,1 , 3 4 , 3 2,1 ]: |
= [4,3 5 , 3 2,1 ]: |
= [3 6,2,1 ]: |
Undergruppeforhold til parakompakte hyperbolske grupper
Disse trærne representerer undergruppeforhold til parakompakte hyperbolske grupper. Undergruppeindekser for hver tilkobling er gitt i rødt. Undergrupper av indeks 2 representerer en speilfjerning og en grunnleggende dobling av domenet. Andre kan utledes av kommensurabilitet (heltal volumforhold) for tetraedriske domener.
| Undergrupper trær | |||
|---|---|---|---|
| H 3 |
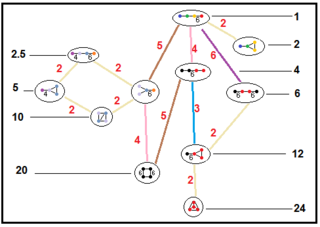
|
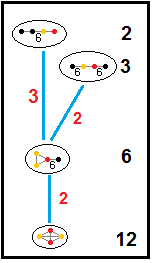
|

|
| H 4 |
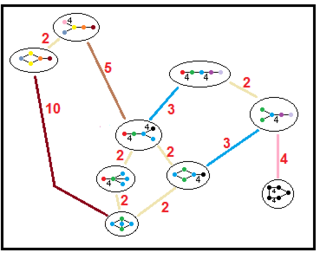
|
||
| H 5 |
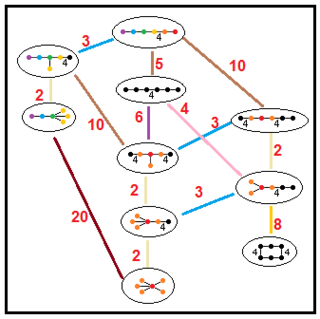
|
||
Hypercompact Coxeter -grupper (Vinberg -polytoper)
Akkurat som det hyperbolske planet H 2 har nontriangular polygonale domener, finnes også høyere-dimensjonale reflekterende hyperbolske domener. Disse ikke-komplekse domenene kan betraktes som degenererte forenklinger med ikke-kryssende speil gitt uendelig rekkefølge, eller i et Coxeter-diagram får slike grener stiplede eller stiplede linjer. Disse ikke -komplekse domenene kalles Vinberg -polytoper , etter Ernest Vinberg for hans Vinbergs algoritme for å finne et ikke -komplekst grunnleggende domene for en hyperbolsk refleksjonsgruppe. Geometrisk kan disse grunnleggende domenene klassifiseres som firkantede pyramider , eller prismer eller andre polytoper med kanter som skjæringspunktet mellom to speil med dihedrale vinkler som π/n for n = 2,3,4 ...
I et simplex-basert domene er det n +1 speil for n-dimensjonalt rom. I ikke-simplex domener er det mer enn n +1 speil. Listen er begrenset, men ikke helt kjent. I stedet er det oppregnet delelister som n + k -speil for k som 2,3 og 4.
Hypercompact Coxeter -grupper i tredimensjonalt rom eller høyere skiller seg fra todimensjonale grupper på en vesentlig måte. To hyperbolske n-goner som har samme vinkler i samme sykliske rekkefølge kan ha forskjellige kantlengder og er generelt ikke kongruente . I kontrast Vinberg -polytoper i 3 dimensjoner eller høyere er helt bestemt av dihedralvinklene. Dette faktum er basert på Mostow -stivhetsteoremet , at to isomorfe grupper generert av refleksjoner i H n for n> = 3, definerer kongruente grunnleggende domener (Vinberg -polytoper).
Vinberg -polytoper med rang n+2 for n dimensjonalt rom
Den komplette listen over kompakte hyperbolske Vinberg-polytoper med rang n+2 speil for n-dimensjoner har blitt oppregnet av F. Esselmann i 1996. En delvis liste ble publisert i 1974 av IM Kaplinskaya.
Den komplette listen over parakompakte løsninger ble publisert av P. Tumarkin i 2003, med dimensjoner fra 3 til 17.
Den minste parakompakte formen i H 3 kan representeres av![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , eller [∞, 3,3, ∞] som kan konstrueres ved en speilfjerning av parakompakt hyperbolisk gruppe [3,4,4] som [3,4,1 + , 4]. Det doble grunnleggende domenet endres fra et tetraeder til en firkantet pyramide. En annen pyramider inkluderer [4,4,1 + , 4] = [∞, 4,4, ∞],
, eller [∞, 3,3, ∞] som kan konstrueres ved en speilfjerning av parakompakt hyperbolisk gruppe [3,4,4] som [3,4,1 + , 4]. Det doble grunnleggende domenet endres fra et tetraeder til en firkantet pyramide. En annen pyramider inkluderer [4,4,1 + , 4] = [∞, 4,4, ∞],![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Hvis du fjerner et speil fra noen av de sykliske hyperboliske koxetergrafene, blir det sløyfe-grafer: [(3,3,4,1 + , 4)] = [((3, ∞, 3)), ((3, ∞, 3 ))] eller
. Hvis du fjerner et speil fra noen av de sykliske hyperboliske koxetergrafene, blir det sløyfe-grafer: [(3,3,4,1 + , 4)] = [((3, ∞, 3)), ((3, ∞, 3 ))] eller![]()
![]()
![]()
![]()
![]() , [(3,4,4,1 + , 4)] = [((4, ∞, 3)), ((3, ∞, 4))] eller
, [(3,4,4,1 + , 4)] = [((4, ∞, 3)), ((3, ∞, 4))] eller![]()
![]()
![]()
![]()
![]() , [(4,4,4,1 + , 4)] = [((4, ∞, 4)), ((4, ∞, 4))] eller
, [(4,4,4,1 + , 4)] = [((4, ∞, 4)), ((4, ∞, 4))] eller![]()
![]()
![]()
![]()
![]() .
.
Andre gyldige parakompakte grafer med firkantede pyramide grunnleggende domener inkluderer:
| Dimensjon | Rang | Grafer |
|---|---|---|
| H 3 | 5 |
|
En annen undergruppe [1 + , 4 1,1,1 ] = [∞, 4,1 + , 4, ∞] = [∞ [6] ].![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Vinberg polytoper med rang n+3 for n dimensjonalt rom
Det er et begrenset antall degenererte grunnleggende forenklinger som eksisterer opptil 8-dimensjoner. Den komplette listen over Compact Vinberg-polytoper med rang n+3 speil for n-dimensjoner er oppført av P. Tumarkin i 2004. Disse gruppene er merket med stiplete/brutte linjer for ultraparallelle grener. Den komplette listen over ikke-kompakte Vinberg-polytoper med rang n+3 speil og med et ikke-enkelt toppunkt for n-dimensjoner er blitt oppregnet av Mike Roberts.
For 4 til 8 dimensjoner telles rang 7 til 11 Coxeter -grupper som henholdsvis 44, 16, 3, 1 og 1. Den høyeste ble oppdaget av Bugaenko i 1984 i dimensjon 8, rang 11:
| Dimensjoner | Rang | Saker | Grafer | ||
|---|---|---|---|---|---|
| H 4 | 7 | 44 | ... | ||
| H 5 | 8 | 16 | .. | ||
| H 6 | 9 | 3 |
|
|
|
| H 7 | 10 | 1 |
|
||
| H 8 | 11 | 1 |
|
||
Vinberg polytoper med rang n+4 for n dimensjonalt rom
Det er et begrenset antall degenererte grunnleggende forenklinger som eksisterer opptil 8-dimensjoner. Kompakte Vinberg-polytoper med rang n+4 speil for n-dimensjoner har blitt utforsket av A. Felikson og P. Tumarkin i 2005.
Lorentziske grupper
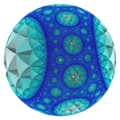 {3,3,7} sett utenfor Poincare -ballmodellen |
 {7,3,3} sett utenfor Poincare -ballmodellen |
Lorentziske grupper for simplex -domener kan defineres som grafer utover de parakompakte hyperbolske formene. Disse kalles noen ganger super-ideelle forenklinger og er også relatert til en Lorentzian-geometri , oppkalt etter Hendrik Lorentz innen spesiell og generell relativitetstid- rom, som inneholder en (eller flere) tidslignende dimensjonale komponenter hvis selvpunktprodukter er negative . Danny Calegari kaller disse konvekse kokompakte Coxeter-gruppene i n-dimensjonalt hyperbolsk rom.
Nivå 2
Et papir fra 1982 av George Maxwell, Sphere Packings and Hyperbolic Reflection Groups , oppregner den endelige listen over Lorentzian av rang 5 til 11. Han kaller dem nivå 2 , noe som betyr at fjerning av alle permutasjoner av 2 noder etterlater en endelig eller euklidisk graf.
Alle Coxeter-grupper i høyere orden av rang-4 er Lorentzian, og ender med grensen som en komplett graf 3- Coxeter-Dynkin-diagram med simplex med 6 uendelige grener, som kan uttrykkes som [∞ [3,3] ]. Rang 5-11 har et begrenset antall grupper henholdsvis 186, 66, 36, 13, 10, 8 og 4 Lorentzian-grupper.
Et papir fra 2013 av H. Chen og J.-P. Labbé, Lorentzian Coxeter-grupper og Boyd-Maxwell-ballpakninger , beregnet og publiserte den komplette listen, og la til 3 nye grupper av rang 5, 189 totalt.
Dette er den komplette listen, inkludert grafikk for rangene 5 til 7.
Svært utvidede coxeter-diagrammer
Én bruk inkluderer en meget utvidet definisjon fra den direkte Dynkin-diagrambruken , som anser affinegrupper som utvidede , hyperbolske grupper for utvidede og en tredje node som svært utvidede enkle grupper. Disse utvidelsene er vanligvis markert med en eksponent på 1,2 eller 3 + symboler for antall utvidede noder. Denne utvidende serien kan utvides bakover, ved å sekvensielt fjerne nodene fra samme posisjon i grafen, selv om prosessen stopper etter at forgreningsnoden er fjernet. Den E 8 utvidede familien er den mest vanlig viste eksempel strekker seg bakover fra E 3 og fremover til E 11 .
Den forlengende prosessen kan definere en begrenset serie Coxeter -grafer som går fra begrenset til affin til hyperbolsk til Lorentzian. Determinanten for Cartan -matrisene bestemmer hvor serien endres fra endelig (positiv) til affin (null) til hyperbolsk (negativ), og slutter som en Lorentzian -gruppe, som inneholder minst en hyperbolsk undergruppe. De noncrystalographic H n -grupper danner en utvidet serie hvor H 4 er utvidet som en kompakt hyperbolsk og over-utvidet til en Lorentzian gruppe.
Determinanten for Schläfli -matrisen etter rangering er:
- det (A 1 n = [2 n-1 ]) = 2 n (Endelig for alle n)
- det (A n = [3 n-1 ]) = n+1 (Endelig for alle n)
- det (B n = [4,3 n-2 ]) = 2 (Endelig for alle n)
- det (D n = [3 n-3,1,1 ]) = 4 (Endelig for alle n)
Determinanter for Schläfli -matrisen i eksepsjonelle serier er:
- det ( E n = [3 n-3,2,1 ]) = 9-n (Endelig for E 3 (= A 2 A 1 ), E 4 (= A 4 ), E 5 (= D 5 ), E 6 , E 7 og E 8 , affin på E 9 ( ), hyperbolisk ved E 10 )
- det ([3 n-4,3,1 ]) = 2 (8-n) (Endelig for n = 4 til 7, affin ( ) og hyperbolisk ved n = 8.)
- det ([3 n-4,2,2 ]) = 3 (7-n) (Endelig for n = 4 til 6, affin ( ) og hyperbolisk ved n = 7.)
- det (F n = [3,4,3 n-3 ]) = 5-n (Endelig for F 3 (= B 3 ) til F 4 , affin ved F 5 ( ), hyperbolisk ved F 6 )
- det (G n = [6,3 n-2 ]) = 3-n (Endelig for G 2 , affin ved G 3 ( ), hyperbolisk ved G 4 )
| Avgrenset | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rangering n | [3 [7] , 3 n-7 ] | [4,3 3 , 3 n-6,1 ] | [3 1,1 , 3,3,3 n-6,1 ] | [3 n-5,2,2 ] | [3 [8] , 3 n-8 ] | [4,3 4 , 3 n-7,1 ] | [3 1,1 , 3,3,3,3 n-7,1 ] | [3 n-5,3,1 ] | E n = [3 n-4,2,1 ] |
| 3 | [3 −1,2,1 ] E 3 = A 2 A 1 |
||||||||
| 4 | [3 −1,2,2 ] A 2 2 |
[3 −1,3,1 ] A 3 A 1 |
[3 0,2,1 ] E 4 = A 4 |
||||||
| 5 | [4,3,3,3,3 −1,1 ] B 4 A 1 |
[3 1,1 , 3,3,3 −1,1 ] D 4 A 1 |
[3 0,2,2 ] A 5 |
[3 0,3,1 ] A 5 |
[3 1,2,1 ] E 5 = D 5 |
||||
| 6 | [3 5 ] A 6 |
[4,3 4 ] B 6 |
[3 1,1 , 3,3,3] D 6 |
[3 1,2,2 ] E 6 |
[4,3,3,3,3,3 −1,1 ] B 5 A 1 |
[3 1,1 , 3,3,3,3 −1,1 ] D 5 A 1 |
[3 1,3,1 ] D 6 |
[3 2,2,1 ] E 6 * |
|
| 7 | [3 [7] ] A 6 + = |
[4,3 3 , 3 1,1 ] B 6 + = |
[3 1,1 , 3,3,3 1,1 ] D 6 + = |
[3 2,2,2 ] E 6 + = |
[3 6 ] A 7 |
[4,3 5 ] B 7 |
[3 1,1 , 3,3,3,3 0,1 ] D 7 |
[3 2,3,1 ] E 7 * |
[3 3,2,1 ] E 7 * |
| 8 | [3 [7] , 3] A 6 ++ = |
[4,3 3 , 3 2,1 ] B 6 ++ = |
[3 1,1 , 3,3,3 2,1 ] D 6 ++ = |
[3 3,2,2 ] E 6 ++ = |
[3 [8] ] A 7 + = * |
[4,3 4 , 3 1,1 ] B 7 + = * |
[3 1,1 , 3,3,3,3 1,1 ] D 7 + = * |
[3 3,3,1 ] E 7 + = * |
[3 4,2,1 ] E 8 * |
| 9 | [3 [7] , 3,3] A 6 +++ |
[4,3 3 , 3 3,1 ] B 6 +++ |
[3 1,1 , 3,3,3 3,1 ] D 6 +++ |
[3 4,2,2 ] E 6 +++ |
[3 [8] , 3] A 7 ++ = * |
[4,3 4 , 3 2,1 ] B 7 ++ = * |
[3 1,1 , 3,3,3,3 2,1 ] D 7 ++ = * |
[3 4,3,1 ] E 7 ++ = * |
[3 5,2,1 ] E 9 = E 8 + = * |
| 10 | [3 [8] , 3,3] A 7 +++ * |
[4,3 4 , 3 3,1 ] B 7 +++ * |
[3 1,1 , 3,3,3,3 3,1 ] D 7 +++ * |
[3 5,3,1 ] E 7 +++ * |
[3 6,2,1 ] E 10 = E 8 ++ = * |
||||
| 11 | [3 7,2,1 ] E 11 = E 8 +++ * |
||||||||
| Det (M n ) | 7 (7- n ) | 2 (7- n ) | 4 (7- n ) | 3 (7- n ) | 8 (8- n ) | 2 (8- n ) | 4 (8- n ) | 2 (8- n ) | 9- n |
Geometrisk bretting
| φ A : A Γ -> A Γ ' for endelige typer | |||
|---|---|---|---|
| Γ | Γ ' | Sammenleggbar beskrivelse | Coxeter - Dynkin -diagrammer |
| I 2 ( h ) | Γ (h) | Dihedral bretting |

|
| B n | A 2n | (Jeg, s n ) | |
| D n+1 , A 2n-1 | (A 3 ,+/-ε) | ||
| F 4 | E 6 | (A 3 , ± ε) | |
| H 4 | E 8 | (A 4 , ± ε) | |
| H 3 | D 6 | ||
| H 2 | A 4 | ||
| G 2 | A 5 | (A 5 , ± ε) | |
| D 4 | (D 4 , ± ε) | ||
| φ: A Γ + -> A Γ ' + for affine typer | |||
| Lokalt trivielt |

|
||
| (Jeg, s n ) | |||
| , | (A 3 , ± ε) | ||
| , | (A 3 , ± ε) | ||
| (Jeg, s n ) | |||
| (I, s n ) & (I, s 0 ) | |||
| (A 3 , ε) & (I, s 0 ) | |||
| (A 3 , ε) & (A 3 , ε ') | |||
| (A 3 , -ε) & (A 3 , -ε ') | |||
| (Jeg, s 1 ) | |||
| , | (A 3 , ± ε) | ||
| , | (A 5 , ± ε) | ||
| , | (B 3 , ± ε) | ||
| , | (D 4 , ± ε) | ||
Et Coxeter-Dynkin-diagram (begrenset, affint eller hyperbolisk) som har en symmetri (som tilfredsstiller en betingelse nedenfor) kan kvotieres av symmetrien, noe som gir et nytt, generelt multiplisert snøret diagram, med prosessen kalt " folding ".
For eksempel, ved D 4 -folding til G 2 , peker kanten i G 2 fra klassen til de tre ytre nodene (valens 1), til klassen til den sentrale noden (valens 3). Og E 8 brettes til 2 kopier av H 4 , den andre kopien skaleres med τ .
Geometrisk tilsvarer dette ortogonale fremspring av ensartede polytoper og tessellasjoner. Spesielt kan ethvert begrenset Coxeter-Dynkin-diagram som er enkelt snøret, brettes til I 2 ( h ), hvor h er Coxeter-tallet , som geometrisk tilsvarer en projeksjon til Coxeter-planet .
 Noen få hyperboliske bretter |
Komplekse refleksjoner
Coxeter - Dynkin -diagrammer har blitt utvidet til komplekst rom , C n der noder er enhetlige refleksjoner av periode større enn 2. Noder er merket med en indeks, antatt å være 2 for vanlig reell refleksjon hvis de undertrykkes. Coxeter skriver den komplekse gruppen, p [q] r, som diagram![]()
![]()
![]()
![]()
![]() .
.
En 1-dimensjonal vanlig kompleks polytop i er representert som![]() , med p -hjørner. Den virkelige representasjonen er en vanlig polygon , { s }. Symmetrien er p [] eller
, med p -hjørner. Den virkelige representasjonen er en vanlig polygon , { s }. Symmetrien er p [] eller![]() , bestill s . En enhetlig operatørgenerator for
, bestill s . En enhetlig operatørgenerator for![]() blir sett på som en rotasjon inn med 2π/ p radianer mot klokken , og a
blir sett på som en rotasjon inn med 2π/ p radianer mot klokken , og a![]() edge er skapt av sekvensielle applikasjoner av en enkelt enhetlig refleksjon. En enhetlig refleksjonsgenerator for en 1-polytop med p- hjørner er e 2π i / p = cos (2π/ p ) + i sin (2π/ p ) . Når p = 2, er generatoren e π i = –1, det samme som en punktrefleksjon i det virkelige planet.
edge er skapt av sekvensielle applikasjoner av en enkelt enhetlig refleksjon. En enhetlig refleksjonsgenerator for en 1-polytop med p- hjørner er e 2π i / p = cos (2π/ p ) + i sin (2π/ p ) . Når p = 2, er generatoren e π i = –1, det samme som en punktrefleksjon i det virkelige planet.
I en høyere polytop, p {} eller![]() representerer et p -kantelement, med et 2 -kantet, {} eller
representerer et p -kantelement, med et 2 -kantet, {} eller![]() , som representerer en vanlig ekte kant mellom to hjørner.
, som representerer en vanlig ekte kant mellom to hjørner.
 Komplekse 1-polytoper, |
Aa vanlige komplekse polygoner i , har formen p { q } r eller Coxeter diagram![]()
![]()
![]()
![]()
![]() . Symmetri -gruppen til en vanlig kompleks polygon
. Symmetri -gruppen til en vanlig kompleks polygon![]()
![]()
![]()
![]()
![]() kalles ikke en Coxeter -gruppe , men i stedet en Shephard -gruppe , en type kompleks refleksjonsgruppe . Rekkefølgen til p [ q ] r er .
kalles ikke en Coxeter -gruppe , men i stedet en Shephard -gruppe , en type kompleks refleksjonsgruppe . Rekkefølgen til p [ q ] r er .
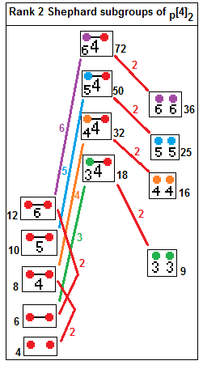
Rang 2 Shephard -gruppene er: 2 [ q ] 2 , p [4] 2 , 3 [3] 3 , 3 [6] 2 , 3 [4] 3 , 4 [3] 4 , 3 [8] 2 , 4 [6] 2 , 4 [4] 3 , 3 [5] 3 , 5 [3] 5 , 3 [10] 2 , 5 [6] 2 og 5 [4] 3 eller![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() av rekkefølge 2 q , 2 p 2 , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 og 1800.
av rekkefølge 2 q , 2 p 2 , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 og 1800.
Symmetri gruppen p 1 [ q ] p 2 er representert av 2 generatorer R 1 , R 2 , hvor: R 1 p 1 = R 2 p 2 = I. Hvis q er jevn, (R 2 R 1 ) q /2 = (R 1 R 2 ) q /2 . Hvis Q er et oddetall, (R 2 R 1 ) (q-1) / 2 R 2 = (R 1 R 2 ) ( q -1) / 2 R- 1 . Når q er odd, er p 1 = p 2 .
den gruppen![]()
![]()
![]() eller [1 1 1] p er definert av 3 periode 2 enhetlige refleksjoner {R 1 , R 2 , R 3 }: R 1 2 = R 1 2 = R 3 2 = (R 1 R 2 ) 3 = (R 2 R 3 ) 3 = (R 3 R 1 ) 3 = (R 1 R 2 R 3 R 1 ) p = 1. Perioden p kan sees på som en dobbel rotasjon i reell .
eller [1 1 1] p er definert av 3 periode 2 enhetlige refleksjoner {R 1 , R 2 , R 3 }: R 1 2 = R 1 2 = R 3 2 = (R 1 R 2 ) 3 = (R 2 R 3 ) 3 = (R 3 R 1 ) 3 = (R 1 R 2 R 3 R 1 ) p = 1. Perioden p kan sees på som en dobbel rotasjon i reell .
En lignende gruppe![]()
![]()
![]() eller [1 1 1] (p) er definert av 3 periode 2 enhetlige refleksjoner {R 1 , R 2 , R 3 }: R 1 2 = R 1 2 = R 3 2 = (R 1 R 2 ) 3 = (R 2 R 3 ) 3 = (R 3 R 1 ) 3 = (R 1 R 2 R 3 R 2 ) p = 1.
eller [1 1 1] (p) er definert av 3 periode 2 enhetlige refleksjoner {R 1 , R 2 , R 3 }: R 1 2 = R 1 2 = R 3 2 = (R 1 R 2 ) 3 = (R 2 R 3 ) 3 = (R 3 R 1 ) 3 = (R 1 R 2 R 3 R 2 ) p = 1.
Se også
- Coxeter -gruppe
- Schwarz trekant
- Goursat tetraeder
- Dynkin -diagram
- Uniform polytop
- Wythoff konstruksjon og Wythoff symbol
Referanser
Videre lesning
- James E. Humphreys, Reflection Groups and Coxeter Groups , Cambridge -studier i avansert matematikk, 29 (1990)
-
Kaleidoskoper: Selected Writings of HSM Coxeter , redigert av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [8] , Googlebooks [ 9]
- (Papir 17) Coxeter , The Evolution of Coxeter-Dynkin-diagrammer , [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
- Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 978-0-486-40919-1 (Kapittel 3: Wythoffs konstruksjon for ensartede polytoper)
-
Coxeter , Regular Polytopes (1963), Macmillan Company
- Regular Polytopes , Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope, and Section 11.3 Representation by graphs)
- HSM Coxeter og WOJ Moser. Generatorer og relasjoner for diskrete grupper 4. utg., Springer-Verlag. New York. 1980
- Norman Johnson , Geometries and Transformations , Chapter 11,12,13, preprint 2011
- NW Johnson , R. Kellerhals , JG Ratcliffe, ST Tschantz, Størrelsen på en hyperbolsk Coxeter simplex , Transformation Groups 1999, Volume 4, Issue 4, pp 329–353 [10] [11]
- Norman W. Johnson og Asia Ivic Weiss kvadratiske heltall og coxeter -grupper PDF Can. J. Math. Vol. 51 (6), 1999 s. 1307–1336
Eksterne linker
- Weisstein, Eric W. "Coxeter - Dynkin -diagram" . MathWorld .
- Oktober 1978 diskusjon om historien til Coxeter -diagrammene av Coxeter og Dynkin i Toronto , Canada ; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library .



![\ venstre [{\ begynne {matrise} 2 og a_ {12} \\ a_ {21} og 2 \ ende {matrise}} \ høyre]](https://wikimedia.org/api/rest_v1/media/math/render/svg/609b9b4324da49c4903330c430b14203d6f971cb)
![\ venstre [{\ begin {smallmatrix} 2 & 0 \\ 0 & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![\ venstre [{\ begin {smallmatrix} 2 & -1 \\-1 & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![{\ displaystyle \ left [{\ begin {smallmatrix} 2 & 1 \\ 1 & 2 \ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
![\ venstre [{\ begin {smallmatrix} 2 &-{\ sqrt {2}} \\-{\ sqrt {2}} & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/934421fb85592c1788a92b7d350953dd2ca94b5e)
![{\ displaystyle \ left [{\ begin {smallmatrix} 2 & {\ sqrt {2}} \\ {\ sqrt {2}} & 2 \ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f92222bfe2eeefe46dddcc56620241d8efd5ef1)
![\ venstre [{\ begin {smallmatrix} 2 &-\ phi \\-\ phi & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/db286eb5ca733d2b6ab1c5f194f03593440b5b3a)

![{\ displaystyle \ left [{\ begin {smallmatrix} 2 & \ phi \\\ phi & 2 \ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dcf61f3b1fac33acafec6ac2d577c66f9f69306)
![{\ displaystyle \ left [{\ begin {smallmatrix} 2 & 1- \ phi \\ 1- \ phi & 2 \ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a16582176db9cb488aa850d0b0a970ff0a62cd6)

![{\ displaystyle \ left [{\ begin {smallmatrix} 2 & \ phi -1 \\\ phi -1 & 2 \ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8548776ee20b1e4a17df57227d372025e5bcbd65)
![\ venstre [{\ begin {smallmatrix} 2 &-{\ sqrt {3}} \\-{\ sqrt {3}} & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b77e92921199a57f051014d4938de1a0d22ef38)
![{\ displaystyle \ left [{\ begin {smallmatrix} 2 & {\ sqrt {3}} \\ {\ sqrt {3}} & 2 \ end {smallmatrix}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51483cac6134b485a8a8ea0d9e2fee62fda6d13a)
![{\ displaystyle \ left [{\ begin {smallmatrix} 2 &-{\ sqrt {2+{\ sqrt {2}}}} \\-{\ sqrt {2+{\ sqrt {2}}}} & 2 \ end {smallmatrix}} \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76feec8c86bbfeb5ce6439e1293efa582074902f)

![{\ displaystyle \ left [{\ begin {smallmatrix} 2 &-{\ sqrt {(5+{\ sqrt {5}})/2}} \\-{\ sqrt {(5+{\ sqrt {5}} )/2}} og 2 \ ende {smallmatrix}} \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cae955a07738bbf5a75ab02e8a5f2597346acaa)

![{\ displaystyle \ left [{\ begin {smallmatrix} 2 &-{\ sqrt {2+{\ sqrt {3}}}} \\-{\ sqrt {2+{\ sqrt {3}}}} & 2 \ end {smallmatrix}} \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f97b80af547d6ad0bcd4cc495671b2f7535d98)

![\ venstre [{\ begin {smallmatrix} 2 & -2 \ cos (\ pi /p) \\-2 \ cos (\ pi /p) & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/71dd5a3c2a3aa08ab89d00e05a0afe4db4876ff8)



![\ venstre [{\ begin {smallmatrix} 2 & -2 \\-2 & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd86323eaf497d2bb96f757556dd458abd5863cf)
![\ venstre [{\ begin {smallmatrix} 2 & -2cosh (2 \ lambda) \\-2cosh (2 \ lambda) & 2 \ end {smallmatrix}} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/274a1c42213fa3aad2dd64c4b63f424d5f3ed349)