Terning - Cube

Vanlig hexahedron
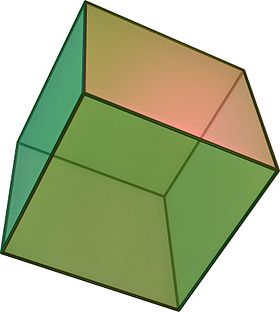(Klikk her for roterende modell)
Type	Platonisk fast stoff
kort kode	4 =
Elementer	F = 6, E = 12 V = 8 (χ = 2)
Ansikter ved sider	6 {4}
Conway -notasjon	C
Schläfli -symboler	{4,3}
	t {2,4} eller {4} × {} tr {2,2} eller {} × {} × {}
Ansiktskonfigurasjon	V3.3.3.3
Wythoff -symbol	3 | 2 4
Coxeter diagram
Symmetri	O h , B 3 , [4,3], (*432)
Rotasjonsgruppe	O , [4,3] + , (432)
Referanser	U 06 , C 18 , W 3
Egenskaper	vanlig , konveks zonohedron
Dihedral vinkel	90 °
4.4.4 ( Vertex -figur )	Octahedron ( dobbelt polyeder )
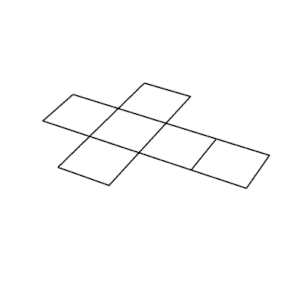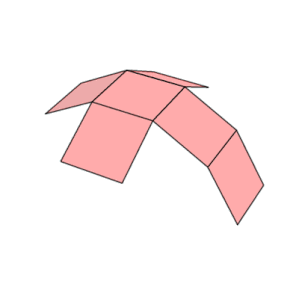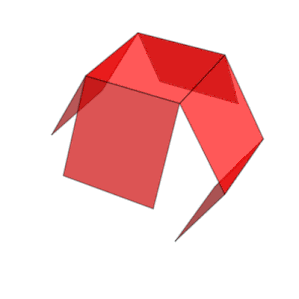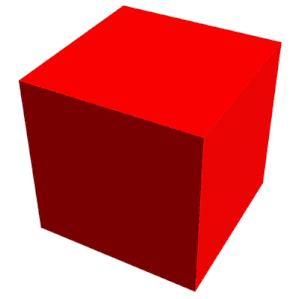
Nett

Nett av en terning

3D -modell av en kube

I geometri er en kube et tredimensjonalt solid objekt avgrenset av seks firkantede flater, fasetter eller sider, med tre som møtes i hvert toppunkt .

Kuben er den eneste vanlige hexahedron og er en av de fem platoniske faste stoffene . Den har 6 flater, 12 kanter og 8 hjørner.

Kuben er også en firkantet parallellpiped , en likesidet kuboid og en høyre romboeder . Det er et vanlig firkantet prisme i tre retninger, og et trigonalt trapezohedron i fire retninger.

Kuben er dobbel i forhold til oktaeder . Den har kubisk eller oktaedrisk symmetri .

Kuben er den eneste konvekse polyederen hvis ansikter alle er firkanter .

Ortogonale anslag

Den kuben har fire spesielle ortogonale projeksjoner , sentrert på et toppunkt, kanter, ansikt og normal til dens toppunkt figuren . Det første og tredje tilsvarer A ₂ og B ₂ Coxeter -flyene .

Ortogonale anslag

Sentrert av	Ansikt	Vertex
Coxeter fly	B 2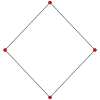	A 2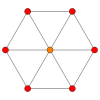
Projektiv symmetri	[4]	[6]
Vinklet utsikt

Sfærisk flislegging

Kuben kan også representeres som en sfærisk flislegging , og projiseres på planet via en stereografisk projeksjon . Denne projeksjonen er konform og bevarer vinkler, men ikke områder eller lengder. Rette linjer på sfæren projiseres som sirkelbuer på flyet.

Ortografisk projeksjon	Stereografisk projeksjon

Kartesiske koordinater

For en terning sentrert ved opprinnelsen, med kanter parallelle med aksene og med en kantlengde på 2, er de kartesiske koordinatene til toppunktene

(± 1, ± 1, ± 1)

mens interiøret består av alle punkter ( x ₀ , x ₁ , x ₂ ) med −1 < x _i <1 for alle i .

Ligning i ${\ displaystyle \ mathbb {R} ^{3}}$

I analytisk geometri , en kube overflate med sentrum ( x ₀ , y ₀ , z ₀ ) og kantlengde på 2a er det geometriske sted for alle punkter ( x , y , z ) slik at

${\ displaystyle \ max \ {| x-x_ {0} |, | y-y_ {0} |, | z-z_ {0} | \} = a.}$

En terning kan også betraktes som det begrensende tilfellet for et 3D -superellipsoid når alle tre eksponentene nærmer seg uendelig.

Formler

For en terning med kantlengde : ${\ displaystyle a}$

flateareal	${\ displaystyle 6a^{2} \,}$	volum	${\ displaystyle a^{3} \,}$
diagonal ansikt	${\ displaystyle {\ sqrt {2}} a}$	plass diagonal	${\ textstyle {\ sqrt {3}} a}$
radius av avgrenset kule	${\ displaystyle {\ frac {\ sqrt {3}} {2}} a}$	kuleradius som tangerer kantene	${\ displaystyle {\ frac {a} {\ sqrt {2}}}}$
radius av innskrevet kule	${\ displaystyle {\ frac {a} {2}}}$	vinkler mellom ansikter (i radianer )	${\ displaystyle {\ frac {\ pi} {2}}}$

Ettersom volumet på en kube er den tredje kraften på sidene , kalles tredjestyrker terninger , analogt med firkanter og andre krefter. ${\ displaystyle a \ times a \ times a}$

En terning har det største volumet blant kuboider (rektangulære esker) med et gitt overflateareal . En kube har også det største volumet blant kuboider med samme totale lineære størrelse (lengde+bredde+høyde).

Punkt i rommet

For en kube hvis omkrets sfæren har radius R , og for et gitt punkt i dets tredimensjonale rom med avstander d _i fra kubens åtte hjørner, har vi:

${\ displaystyle {\ frac {\ sum _ {i = 1}^{8} d_ {i}^{4}} {8}}+{\ frac {16R^{4}} {9}} = \ venstre ({\ frac {\ sum _ {i = 1}^{8} d_ {i}^{2}} {8}}+{\ frac {2R^{2}} {3}} \ høyre)^{ 2}.}$

Doble kuben

Å doble kuben , eller Delian -problemet , var problemet fra gamle greske matematikere med å bare bruke et kompass og rette for å begynne med lengden på kanten av en gitt kube og å konstruere lengden på kanten av en kube med det dobbelte av volumet på den originale kuben. De klarte ikke å løse dette problemet, og i 1837 viste Pierre Wantzel seg at det var umulig fordi kube roten til 2 ikke er et konstruerbart tall .

Ensartede farger og symmetri

Octahedral symmetri tre

Kuben har tre ensartede farger, navngitt etter fargene på de firkantede ansiktene rundt hvert toppunkt: 111, 112, 123.

Kuben har fire klasser av symmetri, som kan representeres av toppunkt-transitive farging av ansiktene. Den høyeste oktaedriske symmetrien O _h har alle ansiktene samme farge. Den dihedral symmetri D _4h kommer fra kuben er et prisme, med alle fire sider er i samme farge. De prismatiske undersettene D _2d har samme farging som den forrige og D _2h har vekslende farger for sidene for totalt tre farger, paret med motsatte sider. Hver symmetriform har et annet Wythoff -symbol .

Navn	Vanlig hexahedron	Firkantet prisme	Rektangulær trapezoprisme	Rektangulær kuboid	Rombisk prisme	Trigonal trapezohedron
Coxeter diagram
Schläfli -symbol	{4,3}	{4} × {} rr {4,2}	s 2 {2,4}	{} 3 tr {2,2}	{} × 2 {}
Wythoff -symbol	3 | 4 2	4 2 | 2		2 2 2 |
Symmetri	O h [4,3] (*432)	D 4t [4,2] (*422)	D 2d [4,2 + ] (2*2)	D 2t [2,2] (*222)		D 3d [6,2 + ] (2*3)
Symmetri rekkefølge	24	16	8	8		12
Bilde (ensartet farging)	(111)	(112)	(112)	(123)	(112)	(111), (112)

Geometriske relasjoner

Kubens 11 garn.

Disse kjente sekssidige terningene er terningformede.

En kube har elleve garn (en vist ovenfor): det vil si at det er elleve måter å flate en hul kube ved å kutte syv kanter. For å farge kuben slik at ikke to tilstøtende ansikter har samme farge, trenger en minst tre farger.

Kuben er cellen til den eneste vanlige flislegging av tredimensjonalt euklidisk rom . Det er også unikt blant de platoniske faststoffene i å ha ansikter med et jevnt antall sider, og følgelig er det det eneste medlemmet i den gruppen som er et zonohedron (hvert ansikt har punktsymmetri).

Terningen kan kuttes i seks identiske firkantede pyramider . Hvis disse firkantede pyramidene deretter er festet til flatene til en andre kube, oppnås en rombisk dodekaeder (med par koplanære trekanter kombinert til rombiske flater).

Andre dimensjoner

Analogen til en kube i det fire-dimensjonale euklidiske rommet har et spesielt navn-en tesseract eller hypercube . Mer riktig er en hyperkube (eller n -dimensjonal kube eller ganske enkelt n -kube) analogen til kuben i n -dimensjonal euklidisk plass og en tesseract er orden -4 hyperkuben. En hyperkube kalles også en målepolytop .

Det er også analoger av kuben i lavere dimensjoner: et punkt i dimensjon 0, et linjestykke i en dimensjon og et kvadrat i to dimensjoner.

Relatert polyeder

Dualen av en terning er en oktaeder , sett her med hjørner i midten av terningens firkantede ansikter.

Den hemicube er det to-til-en kvotient av kuben.

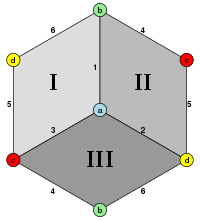
Kvotienten til kuben ved det antipodale kartet gir et projektivt polyeder , hemicube .

Hvis den originale kuben har kantlengde 1, har dens doble polyeder (en oktaeder ) kantlengde . ${\ displaystyle \ scriptstyle {\ sqrt {2}}/2}$

Kuben er et spesialtilfelle i forskjellige klasser av generelle polyeder:

Hodepunktene til en kube kan grupperes i to grupper på fire, som hver danner et vanlig tetraeder ; mer generelt blir dette referert til som en demicube . Disse to danner sammen en vanlig forbindelse , stella octangula . Skjæringspunktet mellom de to danner en vanlig oktaeder. Symmetriene til et vanlig tetraeder tilsvarer de i en kube som tilordner hvert tetraeder til seg selv; de andre symmetriene i kuben kartlegger de to med hverandre.

Ett slikt vanlig tetraeder har et volum på 1/3av kubens. Det gjenværende rommet består av fire like uregelmessige tetraeder med et volum på1/6 av terningen, hver.

Den utbedrede terningen er cuboctahedron . Hvis mindre hjørner blir avskåret får vi et polyeder med seks åttekantede flater og åtte trekantede. Spesielt kan vi få vanlige åttekanter ( avkortet terning ). Den rombkuboktaeder oppnås ved å skjære av begge hjørner og kanter i riktig mengde.

En terning kan skrives inn i en dodekaeder slik at hvert toppunkt i terningen er et toppunkt av dodekaeder og hver kant er en diagonal av et av dodekaederens ansikter; å ta alle slike terninger gir opphav til den vanlige sammensetningen på fem terninger.

Hvis to motsatte hjørner av en kube blir avkortet i dybden av de tre hjørnene som er direkte koblet til dem, oppnås en uregelmessig oktaeder. Åtte av disse uregelmessige oktaeder kan festes til trekantflatene til en vanlig oktaeder for å få kuboktaheder.

Terningen er topologisk relatert til en serie med sfæriske polyeder og fliser med ordre-3 toppunktfigurer .

* n 32 symmetri mutasjon av vanlige fliser: { n , 3} v t e
Sfærisk				Euklidisk	Kompakt hyperb.		Paraco.	Ikke -kompakt hyperbolsk
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

Cuboctahedron er en av en familie av ensartede polyeder relatert til terningen og vanlig oktaeder.

Uniform oktaedrisk polyeder
Symmetri : [4,3], (*432)							[4,3] + (432)	[1 + , 4,3] = [3,3] (*332)		[3 + , 4] (3*2)
{4,3}	t {4,3}	r {4,3} r {3 1,1 }	t {3,4} t {3 1,1 }	{3,4} {3 1,1 }	rr {4,3} s 2 {3,4}	tr {4,3}	sr {4,3}	h {4,3} {3,3}	h 2 {4,3} t {3,3}	s {3,4} s {3 1,1 }
		=	=	=				= eller	= eller	=
Dualer til ensartet polyeder
V4 3	V3.8 2	V (3.4) 2	V4.6 2	V3 4	V3.4 3	V4.6.8	V3 4 .4	V3 3	V3.6 2	V3 5

Kuben er topologisk beslektet som en del av sekvensen av vanlige fliser, som strekker seg inn i det hyperbolske planet : {4, p}, p = 3,4,5 ...

* n 42 symmetri mutasjon av vanlige fliser: {4, n } v t e
Sfærisk	Euklidisk	Kompakt hyperbolsk				Parakompakt
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8} ...	{4, ∞}

Med dihedral symmetri , Dih ₄ , er terningen topologisk beslektet i en serie jevne polyeder og fliser 4.2n.2n, som strekker seg inn i det hyperboliske planet:

* n 42 symmetri mutasjon av avkortede fliser: 4,2 n, 2 n v t e
Symmetri * n 42 [n, 4]	Sfærisk		Euklidisk	Kompakt hyperbolsk				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4] ...	*∞42 [∞, 4]
Avkortede figurer
Konfig.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n-kis- figurer
Konfig.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Alle disse figurene har oktaedrisk symmetri .

Kuben er en del av en sekvens av rombiske polyeder og fliser med [ n , 3] Coxeter -gruppesymmetri. Kuben kan sees på som en rombisk hexahedron hvor romber er firkanter.

Symmetri -mutasjoner av dobbeltkvasiregulære fliser: V (3.n) 2
*n32	Sfærisk			Euklidisk	Hyperbolsk
	*332	*432	*532	*632	*732	*832 ...	*∞32
Flislegging
Konf.	V (3.3) 2	V (3.4) 2	V (3.5) 2	V (3.6) 2	V (3.7) 2	V (3.8) 2	V (3.∞) 2

Kuben er et firkantet prisme :

Familie av ensartede n -gonale prismer

• v
• t
• e

Prisme navn	Digonal prisme	(Trigonal) Trekantprisme	(Tetragonal) Firkantet prisme	Femkantet prisme	Sekskantet prisme	Heptagonal prisme	Åttekantet prisme	Enneagonal prisme	Dekagonalt prisme	Hendekagonal prisme	Dodekagonal prisme	...	Apeirogonal prisme
Polyhedron -bilde												...
Sfærisk flisebilde												Bilde av fliser
Vertex -konfigurasjon.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Som en trigonal trapezohedron er terningen relatert til den sekskantede dihedrale symmetri -familien.

Uniform sekskantet dihedral sfærisk polyeder
Symmetri : [6,2] , (*622)							[6,2] + , (622)	[6,2 + ], (2*3)
{6,2}	t {6,2}	r {6,2}	t {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	s {2,6}
Dualer til uniformer
V6 2	V12 2	V6 2	V4.4.6	V2 6	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Vanlige og ensartede forbindelser av terninger

Sammensetning av tre terninger

Sammensetning av fem terninger

I ensartede honningkaker og polychora

Det er et element av 9 av 28 konvekse jevne honningkaker :

Kubisk honningkake	Avkortet firkantet prismatisk honningkake	Snub firkantet prismatisk honningkake	Langstrakt trekantet prismatisk honningkake	Gyroforlenget trekantet prismatisk honningkake
Cantellated cubic honeycomb	Kantrankert kubisk honningkake	Runcitruncated cubic honeycomb	Runkinert vekslet kubisk honningkake

Det er også et element i fem fire-dimensjonale uniforme polychora :

Tesseract	16-cellers kantellert	Runnet tesseract	Kantrunket 16-cellers	Runcitruncated 16-cell

Kubisk graf

Kubisk graf
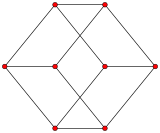Oppkalt etter	Q 3
Hjørner	8
Kanter	12
Radius	3
Diameter	3
Omkrets	4
Automorfismer	48
Kromatisk tall	2
Egenskaper	Hamiltonsk , vanlig , symmetrisk , avstands-vanlig , avstand-transitiv , 3-toppunkt-tilkoblet , todelt , plan graf
Tabell over grafer og parametere

Den skjelett av terningen (-punktene og kanter) danner en graf , med topp-punkt 8 og 12 kanter. Det er et spesielt tilfelle av hyperkubegrafen . Det er en av 5 platoniske grafer , hver et skjelett av sitt platoniske faste stoff .

En utvidelse er den tredimensjonale k -ary Hamming -grafen , som for k = 2 er terninggrafen. Denne typen grafer forekommer i teorien om parallellbehandling i datamaskiner.

Se også

• Pyramide
• Tesseract
• Trapezohedron

Referanser

Eksterne linker

• Weisstein, Eric W. "Cube" . MathWorld .
• Cube: Interactive Polyhedron Model *
• Volum av en kube , med interaktiv animasjon
• Cube (Robert Webbs nettsted)