Bølgepakke - Wave packet

En bølgepakke uten spredning (ekte eller imaginær del)

En bølgepakke med spredning

I fysikken er en bølgepakke (eller bølgetog ) en kort "burst" eller " konvolutt " av lokalisert bølgehandling som beveger seg som en enhet. En bølgepakke kan analyseres til, eller kan syntetiseres fra, et uendelig sett med komponent -sinusformede bølger av forskjellige bølgetall , med faser og amplituder slik at de bare forstyrrer konstruktivt over et lite romområde og destruktivt andre steder. Hver komponent bølgefunksjon , og dermed bølgepakke, er oppløsninger av en bølgeligningen . Avhengig av bølgelikningen kan bølgepakkens profil forbli konstant (ingen spredning , se figur) eller den kan endre seg (spredning) mens den forplanter seg.

Kvantemekanikken tilskriver bølgepakken en spesiell betydning; det tolkes som en sannsynlighetsamplitude , normen i kvadrat som beskriver sannsynlighetstettheten for at en eller flere partikler i en bestemt tilstand skal måles for å ha en gitt posisjon eller momentum. Bølgelegningen er i dette tilfellet Schrödinger -ligningen , og gjennom dens anvendelse er det mulig å utlede tidsutviklingen til et kvantemekanisk system, som ligner på prosessen med den hamiltonske formalismen i klassisk mekanikk . Den spredende karakteren til løsningene i Schrödinger -ligningen har spilt en viktig rolle i å avvise Schrödingers originale tolkning og godta Born -regelen .

I koordinatrepresentasjonen av bølgen (for eksempel det kartesiske koordinatsystemet ), er posisjonen til det fysiske objektets lokaliserte sannsynlighet spesifisert av posisjonen til pakkeløsningen. Dessuten, jo smalere den romlige bølgepakken, og derfor bedre lokalisert posisjonen til bølgepakken, desto større spredning i bølgens momentum . Denne avveiningen mellom spredning i posisjon og spredning i momentum er et karakteristisk trekk ved Heisenberg usikkerhetsprinsipp , og vil bli illustrert nedenfor.

Historisk bakgrunn

På begynnelsen av 1900 -tallet ble det tydelig at klassisk mekanikk hadde noen store feil. Isaac Newton foreslo opprinnelig ideen om at lys kom i separate pakker, som han kalte legemer , men den bølgelignende oppførselen til mange lysfenomener førte raskt til at forskere favoriserte en bølgebeskrivelse av elektromagnetisme . Det var først på 1930 -tallet at lysets partikkelenes natur virkelig begynte å bli allment akseptert innen fysikk. Utviklingen av kvantemekanikk - og suksessen med å forklare forvirrende eksperimentelle resultater - var roten til denne aksept. Således er et av de grunnleggende begrepene i formuleringen av kvantemekanikk det av lys som kommer i diskrete bunter som kalles fotoner . Energien til et foton er en funksjon av dens frekvens,

{\ displaystyle E = h \ nu.}

Fotonens energi er lik Plancks konstant , $h$ , multiplisert med frekvensen, $ν$ . Dette løste et problem i klassisk fysikk, kalt ultrafiolett katastrofe .

Kvantemekanikkens ideer fortsatte å bli utviklet gjennom det 20. århundre. Bildet som ble utviklet var av en partikkelformet verden, med alle fenomener og materie laget av og samspill med diskrete partikler; Imidlertid ble disse partiklene beskrevet av en sannsynlighetsbølge. Interaksjonene, stedene og hele fysikken vil bli redusert til beregningene av disse sannsynlighetsamplituder.

Verdens partikkellignende natur har blitt bekreftet ved forsøk i over et århundre, mens de bølgelignende fenomenene kan karakteriseres som konsekvenser av bølgepakkeaspektet til kvantepartikler (se bølge-partikkeldualitet ). I henhold til prinsippet om komplementaritet manifesterer de bølgelignende og partikkellignende egenskapene seg aldri på samme tid, dvs. i samme eksperiment; se imidlertid Afshar -eksperimentet og den livlige diskusjonen rundt det.

Grunnleggende atferd

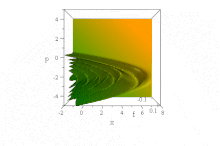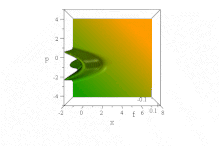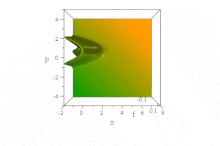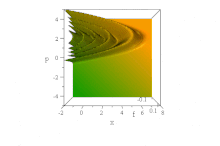
Posisjon plass sannsynlighetstetthet for en opprinnelig gaussisk tilstand fanget i en uendelig potensial som godt opplever periodisk kvantetunnel i en sentrert potensiell vegg.

Ikke-spredende

Som et eksempel på forplantning uten spredning , bør du vurdere bølgeløsninger til den følgende bølgelikningen fra klassisk fysikk

{\ displaystyle {\ partiell ^{2} u \ over \ delvis t ^{2}} = c ^{2} \, \ nabla ^{2} u,}

hvor $c$ er hastigheten på bølgens forplantning i et gitt medium.

Ved hjelp av den fysiske tid konvensjon, $exp (- iωt)$ , har bølgeligningen plan-bølge -løsninger

{\ displaystyle u (\ mathbf {x}, t) = e^{i {(\ mathbf {k \ cdot x}}-\ omega t)},}

hvor

{\ displaystyle \ omega^{2} = | \ mathbf {k} |^{2} c^{2},}

og

{\ displaystyle | \ mathbf {k} |^{2} = k_ {x}^{2}+k_ {y}^{2}+k_ {z}^{2}.}

Dette forholdet mellom $ω$ og $k$ bør være gyldig slik at planbølgen er en løsning på bølgelikningen. Det kalles et spredningsforhold .

For å forenkle, vurder bare bølger som forplanter seg i en dimensjon (utvidelse til tre dimensjoner er grei). Da er den generelle løsningen

{\ displaystyle u (x, t) = Ae^{i (kx- \ omega t)}+Be^{-i (kx+\ omega t)},}

der vi kan ta $ω = kc$ . Det første uttrykket representerer en bølge som forplanter seg i den positive $x$ -retningen siden den bare er en funksjon av $x$ -ct ; det andre uttrykket, som er en funksjon av $x + ct$ , representerer en bølge som forplanter seg i den negative $x$ -retningen .

En bølgepakke er en lokal forstyrrelse som skyldes summen av mange forskjellige bølgeformer . Hvis pakken er sterkt lokalisert, er det nødvendig med flere frekvenser for å tillate konstruktiv superposisjon i lokaliseringsområdet og destruktiv superposisjon utenfor regionen. Fra de grunnleggende løsningene i en dimensjon kan en generell form for en bølgepakke uttrykkes som

{\ displaystyle u (x, t) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {-\ infty}^{\, \ infty} A (k) ~ e^{i (kx- \ omega (k) t)} \, dk.}

Som i flybølgetilfellet beveger bølgepakken seg til høyre for $ω (k) = kc$ , siden $u (x, t) = F (x-ct)$ , og til venstre for $ω (k) = -kc$ , siden $u (x, t) = F (x + ct)$ .

Faktoren 1 ⁄ √ 2π kommer fra Fourier -transformasjonskonvensjoner . Amplituden $A (k)$ inneholder koeffisientene for den lineære superposisjonen til planbølgeløsningene. Disse koeffisientene kan igjen uttrykkes som en funksjon av $u (x, t)$ evaluert ved $t = 0$ ved å invertere Fourier -transformasjonsforholdet ovenfor:

{\ displaystyle A (k) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {-\ infty}^{\, \ infty} u (x, 0) ~ e^{- ikx} \, dx.}

For eksempel å velge

{\ displaystyle u (x, 0) = e^{-x^{2}+ik_ {0} x},}

vi oppnår

{\ displaystyle A (k) = {\ frac {1} {\ sqrt {2}}} e^{-{\ frac {(k-k_ {0})^{2}} {4}}},}

og endelig

{\ displaystyle {\ begin {justert} u (x, t) & = e^{-(x-ct)^{2}+ik_ {0} (x-ct)} \\ & = e^{-( x-ct)^{2}} \ venstre [\ cos \ venstre (2 \ pi {\ frac {x-ct} {\ lambda}} \ høyre)+i \ sin \ venstre (2 \ pi {\ frac { x-ct} {\ lambda}} \ høyre) \ høyre]. \ ende {justert}}}

Den ikke -spredte forplantningen av den virkelige eller imaginære delen av denne bølgepakken presenteres i animasjonen ovenfor.

Spredt

Plasser rom sannsynlighetstetthet for en opprinnelig Gauss -tilstand som beveger seg i en dimensjon ved minimalt usikker, konstant fart i ledig plass.

Derimot, som et eksempel på forplantning nå med spredning , bør du i stedet vurdere løsninger på Schrödinger -ligningen (med m og ħ satt lik en),

{\ displaystyle i {\ partiell \ psi \ over \ delvis t} =-{\ frac {1} {2}} {\ nabla ^{2} \ psi},}

gir spredningsforholdet

{\ displaystyle \ omega = {\ frac {1} {2}} | \ mathbf {k} |^{2}.}

Igjen, ved å begrense oppmerksomheten til én dimensjon, er løsningen på Schrödinger -ligningen som tilfredsstiller den opprinnelige tilstanden , som representerer en bølgepakke lokalisert i verdensrommet ved opprinnelsen, ${\ displaystyle ~ \ psi (x, 0) = {\ sqrt [{4}] {2/\ pi}} \ exp ({-x^{2}+ik_ {0} x})}$

{\ displaystyle {\ begynne {justert} \ psi (x, t) & = {\ frac {\ sqrt [{4}] {2/\ pi}} {\ sqrt {1+2it}}} e^{- {\ frac {1} {4}} k_ {0}^{2}} ~ e^{-{\ frac {1} {1+2it}} \ venstre (x-{\ frac {ik_ {0}} {2}} \ høyre)^{2}} \\ & = {\ frac {\ sqrt [{4}] {2/\ pi}} {\ sqrt {1+2it}}} e^{-{\ frac {1} {1+4t^{2}}} (x-k_ {0} t)^{2}} ~ e^{i {\ frac {1} {1+4t^{2}}} \ venstre ((k_ {0}+2tx) x-{\ frac {1} {2}} tk_ {0}^{2} \ høyre)} ~. \ ende {justert}}}

Et inntrykk av den spredte oppførselen til denne bølgepakken oppnås ved å se på sannsynlighetstettheten:

{\ displaystyle | \ psi (x, t) |^{2} = {\ frac {\ sqrt {2/\ pi}} {\ sqrt {1+4t^{2}}}} ~ e^{-{ \ frac {2 (x-k_ {0} t)^{2}} {1+4t^{2}}}} ~.}

Det er tydelig at denne dispergerende bølgepakken, mens den beveger seg med konstant gruppehastighet $k o$ , delokaliserer seg raskt: den har en bredde som øker med tiden som $\sqrt 1 + 4 t ² \to 2 t$ , så til slutt diffunderer den til et ubegrenset område av rommet .

Momentumprofilen $A (k)$ forblir invariant. Den sannsynligheten nåværende er

{\ displaystyle j = \ rho v = {\ frac {1} {2i}} (\ psi ^{*} \ nabla \ psi -\ psi \ nabla \ psi ^{*}) = \ rho \ left (k_ { 0}+{\ frac {4t (x-k_ {0} t)} {1+4t^{2}}} \ høyre).}

Gaussiske bølgepakker i kvantemekanikk

Superposisjon av 1D -planbølger (blå) som summerer for å danne en kvante Gauss -bølgepakke (rød) som forplanter seg til høyre mens den sprer seg. Blå prikker følger hver planbølges fasehastighet mens den røde linjen følger den sentrale gruppehastigheten.

Posisjon plass sannsynlighetstetthet for en opprinnelig gaussisk tilstand fanget i et uendelig potensial som godt opplever periodisk kvantetunnel i en sentrert potensiell vegg.

1D Gaussian wave -pakke, vist i det komplekse planet, for

a

= 2 og

k

= 4

Ovennevnte dispersive Gauss -bølgepakke, unormalisert og bare sentrert ved opprinnelsen, i stedet, ved $t$ = 0, kan nå skrives i 3D, nå i standard enheter:

{\ displaystyle \ psi (\ mathbf {r}, 0) = e^{-\ mathbf {r} \ cdot \ mathbf {r} /2a},}

hvor $a$ er et positivt reelt tall, kvadratet av bredden på bølgepakken ,

{\ displaystyle a = 2 \ langle \ mathbf {r} \ cdot \ mathbf {r} \ rangle /3 \ langle 1 \ rangle = 2 (\ Delta x)^{2}.}

Fouriertransformasjonen er også en gaussisk når det gjelder bølgetall, $t$ = 0, k -vektoren, (med invers bredde,

{\ displaystyle 1/a = 2 \ langle \ mathbf {k} \ cdot \ mathbf {k} \ rangle/3 \ langle 1 \ rangle = 2 (\ Delta p_ {x}/\ hbar)^{2},}

så det

{\ displaystyle \ Delta x \ Delta p_ {x} = \ hbar /2,}

det metter usikkerhetsforholdet ),

{\ displaystyle \ psi (\ mathbf {k}, 0) = (2 \ pi a)^{3/2} e^{-a \ mathbf {k} \ cdot \ mathbf {k} /2}.}

Hver separate bølge fase-roterer bare i tid, slik at den tidsavhengige Fourier-transformerte løsningen er

${\ displaystyle {\ begynne {justert} \ Psi (\ mathbf {k}, t) & = (2 \ pi a)^{3/2} e^{-a \ mathbf {k} \ cdot \ mathbf {k } /2} e^{-iEt /\ hbar} \\ & = (2 \ pi a)^{3/2} e^{-a \ mathbf {k} \ cdot \ mathbf {k} /2-i (\ hbar^{2} \ mathbf {k} \ cdot \ mathbf {k}/2m) t/\ hbar} \\ & = (2 \ pi a)^{3/2} e^{-(a+ i \ hbar t /m) \ mathbf {k} \ cdot \ mathbf {k} /2}.\end{aligned}}}$

Den inverse Fourier -transformasjonen er fremdeles en Gauss, men nå er parameteren $a$ blitt kompleks, og det er en generell normaliseringsfaktor.

${\ displaystyle \ Psi (\ mathbf {r}, t) = \ left ({a \ over a+i \ hbar t/m} \ right)^{3/2} e^{-{\ mathbf {r} \ cdot \ mathbf {r} \ over 2 (a+i \ hbar t/m)}}.}$

Integralet av $Ψ$ over hele rommet er invariant, fordi det er det indre produktet av $Ψ$ med tilstanden null energi, som er en bølge med uendelig bølgelengde, en konstant funksjon av rommet. For enhver energi -egenstat $η (x)$ , det indre produktet,

{\ displaystyle \ langle \ eta | \ psi \ rangle = \ int \ eta (\ mathbf {r}) \ psi (\ mathbf {r}) d^{3} \ mathbf {r},}

endres bare i tid på en enkel måte: fasen roterer med en frekvens bestemt av energien til $η$ . Når $η$ har null energi, som den uendelige bølgelengdebølgen, endres det ikke i det hele tatt.

Den integrerte $\int | Ψ | 2 d 3 r$ er også invariant, som er en uttalelse om bevaring av sannsynlighet. Eksplisitt,

${\ displaystyle P (r) = | \ Psi |^{2} = \ Psi^{*} \ Psi = \ venstre ({a \ over {\ sqrt {a^{2}+(\ hbar t/m) ^{2}}}} \ høyre)^{3} ~ e^{-{a \, \ mathbf {r} \ cdot \ mathbf {r} \ over a^{2}+(\ hbar t/m) ^{2}}},}$

der √ $a$ er bredden på $P (r)$ ved $t = 0$ ; $r$ er avstanden fra opprinnelsen; partikkelhastigheten er null; og tidsopprinnelsen $t = 0$ kan velges vilkårlig.

Bredden på Gauss er den interessante størrelsen som kan avleses fra sannsynlighetstettheten, $| Ψ | 2$ ,

{\ displaystyle {\ sqrt {a^{2}+(\ hbar t/m)^{2} \ over a}}.}

Denne bredden vokser til slutt lineært i tid, som $ħt/(m\sqrta)$ , noe som indikerer at bølgepakke spres .

For eksempel, hvis en elektronbølgepakke i utgangspunktet er lokalisert i et område med atomdimensjoner (dvs. $10 - 10$ m), fordobles bredden på pakken på omtrent $10 - 16$ s. Det er klart at partikkelbølgepakker sprer seg veldig raskt (i ledig plass): For eksempel, etter $1$ ms, vil bredden ha vokst til omtrent en kilometer.

Denne lineære veksten gjenspeiler den (tidsinvariante) momentumusikkerheten: bølgepakken er begrenset til en smal $Δ x = \sqrt a /2$ , og har derfor et momentum som er usikkert (i henhold til usikkerhetsprinsippet ) med mengden $ħ / \sqrt 2 a$ , et spredning i hastigheten på $ħ /m \sqrt 2 a$ , og dermed i fremtiden posisjon med $ħt /m \sqrt 2 a$ . Usikkerhetsforholdet er da en streng ulikhet, veldig langt fra metning, faktisk! Den første usikkerheten $Δ x Δ p = ħ /2$ har nå økt med en faktor $ħt /ma$ (for store $t$ ).

Det luftige bølgetoget

I motsetning til den ovennevnte gaussiske bølgepakken, har det blitt observert at en bestemt bølgefunksjon basert på Airy -funksjoner , formerer seg fritt uten konvoluttdispersjon, og beholder formen. Den akselererer uforvrengt i fravær av et kraftfelt: $ψ$ $= Ai ($ $B$ $($ $x$ $-$ $B$ $³$ $t$ $²)) exp (i$ $B$ $³$ $t$ $($ $x$ $-2$ $B$ $³$ $t$ $²/3))$ . (For enkelhets skyld er $ħ$ = 1, m = 1/2 , og B er en konstant, jf. Ikke -dimensjonalisering .)

Avkortet syn på tidsutvikling for Airy -fronten i faserom. (Klikk for å animere.)

Likevel er det ingen dissonans med Ehrenfest teorem i denne kraft-fri situasjon, fordi staten er både ikke-normalizable og har en udefinert (uendelig) $⟨ x ⟩$ for alle tider. (I den grad det kan være definert, $⟨ p ⟩ = 0$ for alle tider, til tross for den tilsynelatende akselerasjon av fronten).

I faserommet er dette tydelig i den rene tilstanden Wigner quasiprobability -fordeling av dette bølgetoget, hvis form i x og p er variabel etter hvert som tiden skrider frem, men hvis funksjoner akselererer til høyre, ved akselerering av parabolene $B (x - B ³ t ²) + (p/B - tB ²) ² = 0$ ,

{\ displaystyle {\ begin {justert} W (x, p; t) & = W (xB^{3} t^{2}, pB^{3} t; 0) \\ & = {1 \ over 2 ^{1/3} \ pi B} ~ \ mathrm {Ai} \ venstre (2^{2/3} \ venstre (Bx+{p^{2} \ over B^{2}}-2Bpt \ høyre) \ til høyre). \ end {align}}}

Legg merke til momentfordelingen oppnådd ved å integrere over alle $x$ er konstant. Siden dette er sannsynlighetstettheten i momentum , er det tydelig at selve bølgefunksjonen ikke er normaliserbar.

I 2018 ble den første eksperimentelle observasjonen av den kubiske fasen med å akselerere Airy -bølgepakker oppnådd ved et samarbeid mellom forskere fra israelske, tyske og amerikanske universiteter.

Gratis propagator

Den smale bredde grense for den Gaussiske bølge pakke løsning som skal omtales er den frie propagator kjernen $K$ . For andre differensialligninger, er dette vanligvis kalt Green funksjon, men i kvantemekanikken er det tradisjonelt å reservere navnet Greens funksjon for tiden Fourier transform av $K$ .

Tilbake til en dimensjon for enkelhet, med m og ħ satt lik en, når $a$ er den uendelige størrelsen $ε$ , den Gaussiske opprinnelige tilstanden, skalert på nytt slik at integralen er en,

{\ displaystyle \ psi _ {0} (x) = {1 \ over {\ sqrt {2 \ pi \ epsilon}}} e^{-{x^{2} \ over 2 \ epsilon}} \,}

blir en deltafunksjon , $δ (x)$ , slik at tidens evolusjon,

{\ displaystyle K_ {t} (x) = {1 \ over {\ sqrt {2 \ pi (it+\ epsilon)}}} e^{-x^{2} \ over 2it+\ epsilon} \,}

gir propagatoren.

Vær oppmerksom på at en veldig smal innledende bølgepakke umiddelbart blir uendelig bred, men med en fase som er raskere oscillerende ved store verdier på x . Dette kan virke rart - løsningen går fra å være lokalisert på et tidspunkt til å være "overalt" til alle senere tider , men det er en refleksjon av den enorme momentumusikkerheten til en lokalisert partikkel, som forklart ovenfor.

Vær videre oppmerksom på at normen for bølgefunksjonen er uendelig, noe som også er riktig, siden kvadratet til en deltafunksjon er divergerende på samme måte.

Faktoren som involverer $ε$ er en uendelig liten mengde som er der for å sikre at integraler over $K$ er godt definert. I grensen som ε → 0, blir $K$ rent oscillerende, og integraler av $K$ er ikke absolutt konvergente. I resten av denne delen vil den settes til null, men for at alle integrasjonene over mellomstater skal være godt definert, skal grensen ε → 0 bare tas etter at sluttilstanden er beregnet.

Propagatoren er amplituden for å nå punkt x på tidspunktet t , når man starter ved opprinnelsen, x = 0. Ved translasjon invarians er amplituden for å nå et punkt x når du starter på punkt y den samme funksjonen, bare nå oversatt,

{\ displaystyle K_ {t} (x, y) = K_ {t} (xy) = {1 \ over {\ sqrt {2 \ pi it}}} e^{i (xy)^{2} \ over 2t } \ ,.}

I grensen når t er liten, går propagatoren selvfølgelig til en deltafunksjon,

{\ displaystyle \ lim _ {t \ rightarrow 0} K_ {t} (xy) = \ delta (xy) ~,}

men bare i betydningen fordelinger : Integralen av denne mengden multiplisert med en vilkårlig differensierbar testfunksjon gir verdien av testfunksjonen til null.

For å se dette, vær oppmerksom på at integralen over hele rommet til $K$ til enhver tid er lik 1,

{\ displaystyle \ int K_ {t} (x) dx = 1 \ ,,}

siden denne integralen er det indre produktet av K med den ensartede bølgefunksjonen. Men fasefaktoren i eksponenten har et ikke -null romlig derivat overalt bortsett fra opprinnelsen, og så når tiden er liten er det raske faseavbestillinger i det hele tatt unntatt ett punkt. Dette er nøyaktig sant når grensen ε → 0 er tatt helt til slutt.

Så forplantningskjernen er (fremtidig) tidsutvikling av en deltafunksjon, og den er på en måte kontinuerlig: den går til den innledende deltafunksjonen til små tider. Hvis den første bølgefunksjonen er en uendelig smal pigg i posisjon $y$ ,

{\ displaystyle \ psi _ {0} (x) = \ delta (xy) \ ,,}

det blir den oscillerende bølgen,

{\ displaystyle \ psi _ {t} (x) = {1 \ over {\ sqrt {2 \ pi it}}} e^{i (xy)^{2}/2t} \ ,.}

Siden hver funksjon kan skrives som en vektet sum av slike smale pigger,

{\ displaystyle \ psi _ {0} (x) = \ int \ psi _ {0} (y) \ delta (xy) dy \ ,,}

tidsutviklingen for hver funksjon $ψ$ ₀ bestemmes av denne forplantningskjernen $K$ ,

${\ displaystyle \ psi _ {t} (x) = \ int \ psi _ {0} (y) {1 \ over {\ sqrt {2 \ pi it}}} e^{i (xy)^{2} /2t} dy \ ,.}$

Dermed er dette en formell måte å uttrykke den grunnleggende løsningen eller den generelle løsningen på . Tolkningen av dette uttrykket er at amplituden for en partikkel som finnes ved punkt $x$ på tidspunktet $t$ er amplituden den startet ved $y$ , ganger amplituden den gikk fra $y$ til $x$ , summeret over alle mulige utgangspunkt . Med andre ord er det en konvolusjon av kjernen $K$ med den vilkårlige utgangstilstanden $ψ$ ₀ ,

{\ displaystyle \ psi _ {t} = K*\ psi _ {0} \ ,.}

Siden amplituden for å reise fra $x$ til $y$ etter en tid $t$ + $t$ 'kan vurderes i to trinn, følger propagatoren sammensetningsidentiteten,

{\ displaystyle \ int K (xy; t) K (yz; t ') dy = K (xz; t+t') ~,}

som kan tolkes som følger: amplituden for å reise fra $x$ til $z$ i tid $t$ + $t$ 'er summen av amplituden for å reise fra $x$ til $y$ i tiden $t$ , multiplisert med amplituden for å reise fra $y$ til $z$ i tiden $t$ ', oppsummert over alle mulige mellomtilstander y . Dette er en egenskap til et vilkårlig kvantesystem, og ved å dele tiden inn i mange segmenter, tillater det at tidsutviklingen uttrykkes som en stiintegral .

Analytisk fortsettelse til diffusjon

Spredningen av bølgepakker i kvantemekanikk er direkte relatert til spredningen av sannsynlighetstettheter i diffusjon . For en partikkel som går tilfeldig , tilfredsstiller sannsynlighetstetthetsfunksjonen til enhver tid diffusjonsligningen (se også varmeligningen ),

{\ displaystyle {\ delvis \ over \ delvis t} \ rho = {1 \ over 2} {\ delvis ^{2} \ over \ delvis x ^{2}} \ rho ~,}

der faktoren 2, som kan fjernes ved å skalere enten tid eller rom, bare er for enkelhets skyld.

En løsning på denne ligningen er den spredende Gauss,

{\ displaystyle \ rho _ {t} (x) = {1 \ over {\ sqrt {2 \ pi t}}} e^{-x^{2} \ over 2t} ~,}

og siden integralet av ρ _t er konstant mens bredden blir smal til små tider, nærmer denne funksjonen seg en deltafunksjon ved t = 0,

{\ displaystyle \ lim _ {t \ rightarrow 0} \ rho _ {t} (x) = \ delta (x) \,}

igjen bare i betydningen distribusjoner, slik at

{\ displaystyle \ lim _ {t \ rightarrow 0} \ int _ {x} f (x) \ rho _ {t} (x) = f (0) \,}

for enhver jevn testfunksjon $f$ .

Den spredende Gaussian er forplantningskjernen for diffusjonsligningen, og den adlyder konvolusjonsidentiteten ,

{\ displaystyle K_ {t+t '} = K_ {t}*K_ {t'} \ ,,}

som gjør at diffusjon kan uttrykkes som en baneintegral. Propagatoren er eksponenten til en operator $H$ ,

{\ displaystyle K_ {t} (x) = e^{-tH} \ ,,}

som er den uendelige minimale diffusjonsoperatoren,

{\ displaystyle H =-{\ nabla ^{2} \ over 2} \ ,.}

En matrise har to indekser, som i kontinuerlig plass gjør den til en funksjon av $x$ og $x$ '. I dette tilfellet er matriseelementet $K$ bare avhengig av posisjonens forskjell på grunn av oversettelsesinvarians , og et praktisk misbruk av notasjon er å referere til operatøren, matriseelementene og funksjonen til differansen med samme navn:

{\ displaystyle K_ {t} (x, x ') = K_ {t} (x-x') \ ,.}

Oversettelse invarians betyr at kontinuerlig matrisemultiplikasjon,

{\ displaystyle C (x, x '') = \ int _ {x '} A (x, x') B (x ', x' ') \ ,,}

er i hovedsak konvolusjon,

{\ displaystyle C (\ Delta) = C (x-x '') = \ int _ {x '} A (x-x') B (x'-x '') = \ int _ {y} A ( \ Delta -y) B (y) \ ,.}

Eksponensialet kan defineres over et område av t s som inkluderer komplekse verdier, så lenge integraler over forplantningskjernen forblir konvergente,

{\ displaystyle K_ {z} (x) = e^{-zH} \ ,.}

Så lenge den virkelige delen av $z$ er positiv, for store verdier på $x$ , reduseres $K$ eksponentielt, og integraler over $K$ er faktisk absolutt konvergente.

Grensen for dette uttrykket for $z som$ nærmer seg den rene imaginære aksen er Schrödinger -propagatoren ovenfor,