Konveks funksjon - Convex function

Konveks funksjon på et intervall.

En funksjon (i svart) er konveks hvis og bare hvis regionen over grafen (i grønt) er et konveks sett .

En graf over den bivariate konvekse funksjonen x ² + xy + y ² .

I matematikk kalles en virkelig verdi funksjon konveks hvis linjesegmentet mellom to punkter på grafen til funksjonen ikke ligger under grafen mellom de to punktene. Tilsvarende er en funksjon konveks hvis epigrafen (settet med punkter på eller over grafen til funksjonen) er et konveks sett . En to-differensierbar funksjon av en enkelt variabel er konveks hvis og bare hvis den andre derivaten er ikke-negativ på hele domenet. Velkjente eksempler på konvekse funksjoner til en enkelt variabel inkluderer den kvadratiske funksjonen og den eksponensielle funksjonen${\ displaystyle x^{2}}$ ${\ displaystyle e^{x}}$. Enkelt sagt refererer en konveks funksjon til en funksjon som er i form av en kopp , og en konkav funksjon er i form av en hette . ${\ displaystyle \ cup}$${\ displaystyle \ cap}$

Konvekse funksjoner spiller en viktig rolle på mange matematiske områder. De er spesielt viktige i studiet av optimaliseringsproblemer der de kjennetegnes med en rekke praktiske egenskaper. For eksempel har en strengt konveks funksjon på et åpent sett ikke mer enn ett minimum. Selv i uendelige dimensjonale rom, under passende ytterligere hypoteser, fortsetter konvekse funksjoner å tilfredsstille slike egenskaper, og som et resultat er de de mest velforståtte funksjonene i beregningen av variasjoner . I sannsynlighetsteorien er en konveks funksjon som brukes på den forventede verdien av en tilfeldig variabel alltid begrenset over av den forventede verdien av den konvekse funksjonen til den tilfeldige variabelen. Dette resultatet, kjent som Jensens ulikhet , kan brukes til å utlede ulikheter som den aritmetisk -geometriske gjennomsnittlige ulikheten og Hölders ulikhet .

Definisjon

Spill media

Visualisering av en konveks funksjon og Jensens ulikhet

La være en konveks delmengde av et ekte vektorrom og la det være en funksjon. ${\ displaystyle X}$${\ displaystyle f: X \ to \ mathbb {R}}$

Da kalles det konveks hvis og bare hvis noen av følgende tilsvarende betingelser holder: ${\ displaystyle f}$

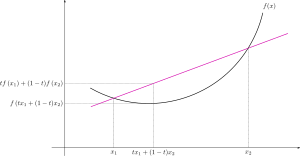
1. For alle og alle : ${\ displaystyle 0 \ leq t \ leq 1}$${\ displaystyle x_ {1}, x_ {2} \ i X}$
   $${\ displaystyle f \ left (tx_ {1}+(1-t) x_ {2} \ right) \ leq tf \ left (x_ {1} \ right)+(1-t) f \ left (x_ {2 }\Ikke sant)}$$

   
   Høyre side representerer den rette linjen mellom og i grafen over som en funksjon av å øke fra til eller minske fra for å feie denne linjen. På samme måte representerer argumentet for funksjonen på venstre side den rette linjen mellom og i eller -aksen på grafen til Så krever denne tilstanden at den rette linjen mellom et par punkter på kurven for å være over eller bare møter grafen. ${\ displaystyle \ left (x_ {1}, f \ left (x_ {1} \ right) \ right)}$${\ displaystyle \ left (x_ {2}, f \ left (x_ {2} \ right) \ right)}$${\ displaystyle f}$${\ displaystyle t;}$${\ displaystyle t}$${\ displaystyle 0}$${\ displaystyle 1}$${\ displaystyle t}$${\ displaystyle 1}$${\ displaystyle 0}$${\ displaystyle f}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle f.}$${\ displaystyle f}$
2. For alle og alle slik at : ${\ displaystyle 0 <t <1}$${\ displaystyle x_ {1}, x_ {2} \ i X}$${\ displaystyle x_ {1} \ neq x_ {2}}$
   $${\ displaystyle f \ left (tx_ {1}+(1-t) x_ {2} \ right) \ leq tf \ left (x_ {1} \ right)+(1-t) f \ left (x_ {2 }\Ikke sant)}$$

   
   Forskjellen på denne andre tilstanden med hensyn til den første tilstanden ovenfor er at denne tilstanden ikke inkluderer skjæringspunktene (f.eks. Og ) mellom den rette linjen som går gjennom et par punkter på kurven til (den rette linjen er representert av på høyre side av denne tilstanden) og kurven for den første tilstanden inkluderer skjæringspunktene når det blir eller ved eller eller Faktisk trenger skjæringspunktene ikke å bli vurdert i en tilstand av konveks bruk${\ displaystyle \ left (x_ {1}, f \ left (x_ {1} \ right) \ right)}$${\ displaystyle \ left (x_ {2}, f \ left (x_ {2} \ right) \ right)}$${\ displaystyle f}$${\ displaystyle f;}$${\ displaystyle f \ left (x_ {1} \ right) \ leq f \ left (x_ {1} \ right)}$${\ displaystyle f \ left (x_ {2} \ right) \ leq f \ left (x_ {2} \ right)}$${\ displaystyle t = 0}$${\ displaystyle 1,}$${\ displaystyle x_ {1} = x_ {2}.}$
   $${\ displaystyle f \ left (tx_ {1}+(1-t) x_ {2} \ right) \ leq tf \ left (x_ {1} \ right)+(1-t) f \ left (x_ {2 }\Ikke sant)}$$

   
   fordi og er alltid sanne (så ikke nyttig å være en del av en tilstand). ${\ displaystyle f \ left (x_ {1} \ right) \ leq f \ left (x_ {1} \ right)}$${\ displaystyle f \ left (x_ {2} \ right) \ leq f \ left (x_ {2} \ right)}$

Den andre setningen som karakteriserer konvekse funksjoner som er verdsatt i den virkelige linjen, er også setningen som brukes til å definere konvekse funksjoner som er verdsatt i den utvidede reelle talllinjen der en slik funksjon er tillatt (men ikke nødvendig) å ta som en verdi. Den første setningen brukes ikke fordi den tillater å ta eller som en verdi, i så fall hvis eller henholdsvis, ville være udefinert (fordi multiplikasjonene og er udefinerte). Summen er også udefinert, så en konveks utvidet real-verdi funksjon er vanligvis bare tillatt å ta nøyaktig en av og som en verdi. ${\ displaystyle \ mathbb {R}}$ ${\ displaystyle [-\ infty, \ infty] = \ mathbb {R} \ cup \ {\ pm \ infty \},}$${\ displaystyle f}$${\ displaystyle \ pm \ infty}$${\ displaystyle t}$${\ displaystyle 0}$${\ displaystyle 1}$${\ displaystyle f \ left (x_ {1} \ right) = \ pm \ infty}$${\ displaystyle f \ left (x_ {2} \ right) = \ pm \ infty,}$${\ displaystyle tf \ left (x_ {1} \ right)+(1-t) f \ left (x_ {2} \ right)}$${\ displaystyle 0 \ cdot \ infty}$${\ displaystyle 0 \ cdot (-\ infty)}$${\ displaystyle -\ infty +\ infty}$${\ displaystyle -\ infty}$${\ displaystyle +\ infty}$

Den andre uttalelsen kan også modifiseres for å få definisjonen på streng konveksitet , der sistnevnte oppnås ved å erstatte den med den strenge ulikheten Eksplisitt kalles kartet strengt konveks hvis og bare hvis for alle virkelige og alt slik at : ${\ displaystyle \, \ leq \,}$${\ displaystyle \, <.}$${\ displaystyle f}$${\ displaystyle 0 <t <1}$${\ displaystyle x_ {1}, x_ {2} \ i X}$${\ displaystyle x_ {1} \ neq x_ {2}}$

$${\ displaystyle f \ left (tx_ {1}+(1-t) x_ {2} \ right) <tf \ left (x_ {1} \ right)+(1-t) f \ left (x_ {2} \Ikke sant)}$$

En strengt konveks funksjon er en funksjon som den rette linjen mellom et par punkter på kurven er over kurven bortsett fra skjæringspunktene mellom den rette linjen og kurven. ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f}$

Funksjonen sies å være konkav (resp. Strengt konkav ) hvis ( multiplisert med -1) er konveks (resp. Strengt konveks). ${\ displaystyle f}$${\ displaystyle -f}$${\ displaystyle f}$

Alternativ navn

Begrepet konveks blir ofte referert til som konveks ned eller konkav oppover , og begrepet konkav blir ofte referert til som konkav ned eller konveks oppover . Hvis begrepet "konveks" brukes uten et "opp" eller "ned" søkeord, refererer det strengt til en koppformet graf . Som et eksempel refererer Jensens ulikhet til en ulikhet som involverer en konveks eller konveks (opp) funksjon. ${\ displaystyle \ cup}$

Egenskaper

Mange egenskaper til konvekse funksjoner har samme enkle formulering for funksjoner med mange variabler som for funksjoner til en variabel. Se egenskapene nedenfor for mange variabler, siden noen av dem ikke er oppført for funksjoner til en variabel.

Funksjoner av en variabel

• Anta er en funksjon av en reell variabel definert på et intervall, og la${\ displaystyle f}$
  $${\ displaystyle R (x_ {1}, x_ {2}) = {\ frac {f (x_ {2})-f (x_ {1})} {x_ {2} -x_ {1}}}}$$

  
  (Merk at er helningen av den lilla linje i den ovennevnte tegning, det funksjons R er symmetrisk i betyr at R ikke er endret ved å bytte og ). er konveks hvis og bare hvis er monotonisk ikke-avtagende i for hver fast (eller vice versa). Denne karakteriseringen av konveksitet er ganske nyttig for å bevise følgende resultater.${\ displaystyle R (x_ {1}, x_ {2})}$${\ displaystyle (x_ {1}, x_ {2}),}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle f}$${\ displaystyle R (x_ {1}, x_ {2})}$${\ displaystyle x_ {1},}$${\ displaystyle x_ {2}}$
• En konveks funksjon av en reell variabel definert på et åpent intervall C er kontinuerlig på tillater venstre og høyre derivater , og disse er monotont ikke-reduserende . Som en konsekvens er den differensierbar i det hele tatt, men høyst mange punkter, men settet som ikke er differensierbart kan imidlertid fortsatt være tett. Hvis er lukket, kan det hende at den ikke er kontinuerlig ved endepunktene til (et eksempel er vist i eksempler -delen ).${\ displaystyle f}$ ${\ displaystyle C.}$ ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle C}$${\ displaystyle f}$${\ displaystyle C}$
• En differensierbar funksjon av en variabel er konveks på et intervall hvis og bare hvis derivatet er monotont ikke-reduserende i det intervallet. Hvis en funksjon er differensierbar og konveks, er den også kontinuerlig differensierbar .
• En differensierbar funksjon av en variabel er konveks på et intervall hvis og bare hvis grafen ligger over alle tangentene :
  $${\ displaystyle f (x) \ geq f (y)+f '(y) (xy)}$$

  
  for alle x og y i intervallet.
• En to ganger differensierbar funksjon av en variabel er konveks på et intervall hvis og bare hvis den andre derivaten er ikke-negativ der; Dette gir en praktisk test for konveksitet. Visuelt "buer en to ganger differensierbar konveks funksjon opp" uten bøyninger den andre veien ( bøyningspunkter ). Hvis dets andre derivat er positivt på alle punkter, er funksjonen strengt konveks, men det motsatte holder ikke. For eksempel er det andre derivatet av is , som er null for, men er strengt konveks. ${\ displaystyle f (x) = x^{4}}$${\ displaystyle f '' (x) = 12x^{2}}$${\ displaystyle x = 0,}$${\ displaystyle x^{4}}$
  • Denne egenskapen og egenskapen ovenfor når det gjelder "... dens derivat er monotont ikke-reduserende ..." er ikke like siden hvis det er ikke-negativt på et intervall , er det monotont ikke-avtagende mens det motsatte ikke er sant, for eksempel, er monotont ikke-avtagende mens dets derivat ikke er definert på noen punkter på .${\ displaystyle f ''}$${\ displaystyle X}$${\ displaystyle f '}$${\ displaystyle X}$${\ displaystyle f '}$${\ displaystyle X}$${\ displaystyle f ''}$${\ displaystyle X}$
• Dersom er en konveks funksjon av en reell variabel, og , så er superadditiv på positiv virkelig , det vil si for positive reelle tall og .${\ displaystyle f}$${\ displaystyle f (0) \ leq 0}$${\ displaystyle f}$${\ displaystyle f (a+b) \ geq f (a)+f (b)}$${\ displaystyle a}$${\ displaystyle b}$

Bevis

Siden er konveks, ved å bruke en av de konvekse funksjonsdefinisjonene ovenfor og la det følge det for alle virkelige${\ displaystyle f}$${\ displaystyle x_ {2} = 0,}$${\ displaystyle 0 \ leq t \ leq 1,}$ $${\ displaystyle f (tx_ {1}) = f (tx_ {1}+(1-t) \ cdot 0) \ leq tf (x_ {1})+(1-t) f (0) \ leq tf ( x_ {1}) \ høyre pil f (tx_ {1}) \ leq tf (x_ {1}).}$$ Av dette følger det $${\ displaystyle f (a)+f (b) = f \ venstre ((a+b) {\ frac {a} {a+b}} \ høyre)+f \ venstre ((a+b) {\ frac {b} {a+b}} \ høyre) \ leq {\ frac {a} {a+b}} f (a+b)+{\ frac {b} {a+b}} f (a+b ) = f (a+b) \ høyre pil f (a)+f (b) \ leq f (a+b).}$$

• En funksjon er midtpunkt konveks på et intervall hvis for alle${\ displaystyle C}$${\ displaystyle x_ {1}, x_ {2} \ i C}$
  $${\ displaystyle f \ left ({\ frac {x_ {1}+x_ {2}} {2}} \ right) \ leq {\ frac {f (x_ {1})+f (x_ {2})}} {2}}.}$$

  
  Denne tilstanden er bare litt svakere enn konveksitet. For eksempel er en virkelig verdsatt Lebesgue-målbar funksjon som er midtpunktskonveks konveks: dette er et teorem om Sierpinski . Spesielt vil en kontinuerlig funksjon som er midtpunktskonveks være konveks.

Funksjoner av flere variabler

• En funksjon verdsatt i de utvidede reelle tallene er konveks hvis og bare hvis den er epigraf${\ displaystyle f: X \ til [-\ infty, \ infty]}$ ${\ displaystyle [-\ infty, \ infty] = \ mathbb {R} \ cup \ {\ pm \ infty \}}$
  $${\ displaystyle \ {(x, r) \ i X \ times \ mathbb {R} ~: ~ r \ geq f (x) \}}$$

  
  er et konveks sett.
• En differensierbar funksjon definert på et konvekst domene er konveks hvis og bare hvis det gjelder for alle i domenet.${\ displaystyle f}$${\ displaystyle f (x) \ geq f (y)+\ nabla f (y) \ cdot (xy)}$${\ displaystyle x, y}$
• En to ganger differensierbar funksjon av flere variabler er konveks på et konveks sett hvis og bare hvis dens hessiske matrise av andre partielle derivater er positiv semidefinitt på innsiden av det konvekse settet.
• For en konveks funksjon er undernivåsettene og med konvekse sett. En funksjon som tilfredsstiller denne egenskapen kalles en kvasikonveks funksjon og kan ikke være en konveks funksjon.${\ displaystyle f,}$ ${\ displaystyle \ {x: f (x) <a \}}$${\ displaystyle \ {x: f (x) \ leq a \}}$${\ displaystyle a \ in \ mathbb {R}}$
• Følgelig er settet med globale minimiserere av en konveks funksjon et konveks sett: - konveks.${\ displaystyle f}$${\ displaystyle {\ operatorname {argmin}} \, f}$
• Et hvilket som helst lokalt minimum for en konveks funksjon er også et globalt minimum . En strengt konveks funksjon vil ha høyst ett globalt minimum.
• Jensens ulikhet gjelder for hver konveks funksjon . Dersom er en tilfeldig variabel tar verdier i domenet for deretter hvor E betegner den matematiske forventning . Faktisk er konvekse funksjoner akkurat de som tilfredsstiller hypotesen om Jensens ulikhet .${\ displaystyle f}$${\ displaystyle X}$${\ displaystyle f,}$${\ displaystyle \ operatorname {E} (f (X)) \ geq f (\ operatorname {E} (X)),}$
• En førsteordens homogen funksjon av to positive variabler og (det vil si en funksjon som tilfredsstiller alle positive reelle ) som er konveks i en variabel, må være konveks i den andre variabelen.${\ displaystyle x}$${\ displaystyle y,}$${\ displaystyle f (ax, ay) = af (x, y)}$${\ displaystyle a, x, y> 0}$

Operasjoner som bevarer konveksitet

• ${\ displaystyle -f}$er konkav hvis og bare hvis den er konveks.${\ displaystyle f}$
• Ikke -negative vektede summer:
  • hvis og er alle konvekse, så er det også . Spesielt er summen av to konvekse funksjoner konveks.${\ displaystyle w_ {1}, \ ldots, w_ {n} \ geq 0}$${\ displaystyle f_ {1}, \ ldots, f_ {n}}$${\ displaystyle w_ {1} f_ {1} +\ cdots +w_ {n} f_ {n}}$
  • Denne egenskapen strekker seg også til uendelige summer, integraler og forventede verdier (forutsatt at de eksisterer).
• Elementvis maksimal: la være en samling av konvekse funksjoner. Da er den konveks. Domenet til er samlingen av punkter der uttrykket er begrenset. Viktige spesialtilfeller: ${\ displaystyle \ {f_ {i} \} _ {i \ i I}}$${\ displaystyle g (x) = \ sup _ {i \ i I} f_ {i} (x)}$${\ displaystyle g (x)}$
  • Hvis det er konvekse funksjoner, så er det det også${\ displaystyle f_ {1}, \ ldots, f_ {n}}$${\ displaystyle g (x) = \ max \ {f_ {1} (x), \ ldots, f_ {n} (x) \}}$
  • Danskins teorem : Hvis er konveks i så er konveks i selv om C ikke er et konveks sett.${\ displaystyle f (x, y)}$${\ displaystyle x}$${\ displaystyle g (x) = \ sup \ nolimits _ {y \ in C} f (x, y)}$${\ displaystyle x}$
• Sammensetning:
  • Hvis f og g er konvekse funksjoner og g er ikke-reduserende over et univariat domene, er det konveks. Som et eksempel, hvis det er konveks, så er det det også . fordi er konveks og monotonisk økende.${\ displaystyle h (x) = g (f (x))}$${\ displaystyle f}$${\ displaystyle e^{f (x)}}$${\ displaystyle e^{x}}$
  • Hvis f er konkav og g er konveks og ikke-økende over et univariat domene, er den konveks.${\ displaystyle h (x) = g (f (x))}$
  • Konveksitet er invariant under affine kart: det vil si at hvis f er konveks med domene , så er det , hvor med domene .${\ displaystyle D_ {f} \ subseteq \ mathbf {R} ^{m}}$${\ displaystyle g (x) = f (Ax+b)}$${\ displaystyle A \ in \ mathbf {R} ^{m \ times n} {\ text {,}} b \ in \ mathbf {R} ^{m}}$${\ displaystyle D_ {g} \ subseteq \ mathbf {R} ^{n}}$
• Minimering: Hvis er konveks i så er konveks i x , forutsatt at C er et konveks sett og at${\ displaystyle f (x, y)}$${\ displaystyle (x, y)}$${\ displaystyle g (x) = \ inf \ nolimits _ {y \ in C} f (x, y)}$${\ displaystyle g (x) \ neq -\ infty}$
• Hvis den er konveks, er perspektivet med domenet konveks.${\ displaystyle f}$${\ displaystyle g (x, t) = tf \ left ({\ tfrac {x} {t}} \ right)}$${\ displaystyle \ left \ lbrace (x, t) \ mid {\ tfrac {x} {t}} \ in \ operatorname {Dom} (f), t> 0 \ right \ rbrace}$

Sterkt konvekse funksjoner

Begrepet sterk konveksitet strekker seg og parametrerer begrepet streng konveksitet. En sterkt konveks funksjon er også strengt konveks, men ikke omvendt.

En differensierbar funksjon kalles sterkt konveks med parameter m > 0 hvis følgende ulikhet gjelder for alle punktene x , y i sitt domene: ${\ displaystyle f}$

$${\ displaystyle (\ nabla f (x)-\ nabla f (y))^{T} (xy) \ geq m \ | xy \ | _ {2}^{2}}$$

$${\ displaystyle \ langle \ nabla f (x)-\ nabla f (y), xy \ rangle \ geq m \ | xy \ |^{2}}$$

funksjoner. ${\ displaystyle \ | \ cdot \ |}$

En tilsvarende betingelse er følgende:

$${\ displaystyle f (y) \ geq f (x)+\ nabla f (x)^{T} (yx)+{\ frac {m} {2}} \ | yx \ | _ {2}^{2 }}$$

Det er ikke nødvendig for en funksjon å være differensierbar for å være sterkt konveks. En tredje definisjon for en sterkt konveks funksjon, med parameter m , er at for alle x , y i domenet og${\ displaystyle t \ in [0,1],}$

$${\ displaystyle f (tx+(1-t) y) \ leq tf (x)+(1-t) f (y)-{\ frac {1} {2}} mt (1-t) \ | xy \ | _ {2}^{2}}$$

Legg merke til at denne definisjonen nærmer seg definisjonen for streng konveksitet som m → 0, og er identisk med definisjonen av en konveks funksjon når m = 0. Til tross for dette finnes det funksjoner som er strengt konvekse, men som ikke er sterkt konvekse for noen m > 0 ( se eksempel nedenfor).

Hvis funksjonen er to ganger kontinuerlig differensierbar, så er den sterkt konveks med parameter

= 0, betyr dette at hessianeren er positiv semidefinitt (eller hvis domenet er den virkelige linjen, betyr det at ), noe som betyr at funksjonen er konveks, og kanskje strengt konveks, men ikke sterkt konveks. ${\ displaystyle f}$${\ displaystyle \ nabla ^{2} f (x) \ succeq mI}$${\ displaystyle \ nabla ^{2} f}$${\ displaystyle \ succeq}$${\ displaystyle \ nabla ^{2} f (x) -mI}$${\ displaystyle \ nabla ^{2} f (x)}$${\ displaystyle \ nabla ^{2} f (x)}$${\ displaystyle f '' (x),}$${\ displaystyle f '' (x) \ geq m}$${\ displaystyle f '' (x) \ geq 0}$

Forutsatt at funksjonen er to ganger kontinuerlig differensierbar, kan man vise at den nedre grensen for innebærer at den er sterkt konveks. Ved å bruke

eksisterer det ${\ displaystyle \ nabla ^{2} f (x)}$

$${\ displaystyle z \ in \ {tx+(1-t) y: t \ in [0,1] \}}$$

slik at

$${\ displaystyle f (y) = f (x)+\ nabla f (x)^{T} (yx)+{\ frac {1} {2}} (yx)^{T} \ nabla^{2} f (z) (yx)}$$

Deretter

$${\ displaystyle (yx)^{T} \ nabla^{2} f (z) (yx) \ geq m (yx)^{T} (yx)}$$

ved antagelsen om egenverdiene, og derfor gjenoppretter vi den andre sterke konveksitetsligningen ovenfor.

En funksjon er sterkt konveks med parameter

hvis og bare hvis funksjonen ${\ displaystyle f}$

$${\ displaystyle x \ mapsto f (x)-{\ frac {m} {2}} \ | x \ |^{2}}$$

er konveks.

Skillet mellom konveks, strengt konveks og sterkt konveks kan være subtil ved første øyekast. Hvis er to ganger kontinuerlig differensierbar og domenet er den virkelige linjen, kan vi karakterisere det som følger: ${\ displaystyle f}$

• ${\ displaystyle f}$konveks hvis og bare hvis for alle

.${\ displaystyle f '' (x) \ geq 0}$

${\ displaystyle f}$strengt konveks hvis for alle

(merk: dette er tilstrekkelig, men ikke nødvendig).${\ displaystyle f '' (x)> 0}$

${\ displaystyle f}$sterkt konveks hvis og bare hvis for alle

.${\ displaystyle f '' (x) \ geq m> 0}$

La oss for eksempel være strengt konvekse, og anta at det er en rekke punkter slik at . Selv om funksjonen ikke er sterkt konveks fordi den vil bli vilkårlig liten. ${\ displaystyle f}$${\ displaystyle (x_ {n})}$${\ displaystyle f '' (x_ {n}) = {\ tfrac {1} {n}}}$${\ displaystyle f '' (x_ {n})> 0}$${\ displaystyle f '' (x)}$

En to ganger kontinuerlig differensierbar funksjon på et kompakt domene som tilfredsstiller for alle, er sterkt konveks. Beviset for denne påstanden følger av

, som sier at en kontinuerlig funksjon på et kompakt sett har et maksimum og minimum. ${\ displaystyle f}$${\ displaystyle X}$${\ displaystyle f '' (x)> 0}$${\ displaystyle x \ i X}$

Sterkt konvekse funksjoner er generelt lettere å arbeide med enn konvekse eller strengt konvekse funksjoner, siden de er en mindre klasse. Som strengt konvekse funksjoner, har sterkt konvekse funksjoner unike minima på kompakte sett.

Uniformt konvekse funksjoner

En jevnt konveks funksjon, med modul , er en funksjon som for alle

tilfredsstiller ${\ displaystyle \ phi}$${\ displaystyle f}$

$${\ displaystyle f (tx+(1-t) y) \ leq tf (x)+(1-t) f (y) -t (1-t) \ phi (\ | xy \ |)}$$

hvor er en funksjon som er ikke-negativ og forsvinner bare ved 0. Dette er en generalisering av begrepet sterkt konveks funksjon; ved å ta gjenoppretter vi definisjonen av sterk konveksitet. ${\ displaystyle \ phi}$${\ displaystyle \ phi (\ alpha) = {\ tfrac {m} {2}} \ alpha ^{2}}$

Eksempler

Funksjoner av en variabel

• Funksjonen har , så

er en konveks funksjon. Den er også sterkt konveks (og dermed strengt konveks også), med sterk konveksitetskonstant 2.${\ displaystyle f (x) = x^{2}}$${\ displaystyle f '' (x) = 2> 0}$

Funksjonen har , så

er en konveks funksjon. Det er strengt konveks, selv om det andre derivatet ikke er strengt positivt på alle punkter. Den er ikke sterkt konveks.${\ displaystyle f (x) = x^{4}}$${\ displaystyle f '' (x) = 12x^{2} \ geq 0}$

Den absolutte verdi funksjon er konveks (som gjenspeiles i den

 = 0. Det er ikke strengt konveks.${\ displaystyle f (x) = | x |}$

Funksjonen for er konveks.${\ displaystyle f (x) = | x |^{p}}$${\ displaystyle p \ geq 1}$

Den eksponensielle funksjonen er konveks. Det er også strengt konveks siden , men det er ikke sterkt konveks siden det andre derivatet kan være vilkårlig nær null. Mer generelt funksjonen er

er en konveks funksjon. Begrepet "superkonveks" brukes noen ganger i stedet.${\ displaystyle f (x) = e^{x}}$${\ displaystyle f '' (x) = e^{x}> 0}$${\ displaystyle g (x) = e^{f (x)}}$

Funksjonen med domenet [0,1] definert av for er konveks; den er kontinuerlig på det åpne intervallet (0, 1), men ikke kontinuerlig ved 0 og 1.${\ displaystyle f}$${\ displaystyle f (0) = f (1) = 1, f (x) = 0}$${\ displaystyle 0 <x <1}$

Funksjonen x ³ har andre derivat 6 x ; dermed er den konveks på settet der x ≥ 0 og konkav på settet der  x  ≤ 0.

Eksempler på funksjoner som er monotont økende, men ikke konvekse, inkluderer og .${\ displaystyle f (x) = {\ sqrt {x}}}$${\ displaystyle g (x) = \ log x}$

Eksempler på funksjoner som er konvekse, men ikke monotont økende, inkluderer og .${\ displaystyle h (x) = x^{2}}$${\ displaystyle k (x) =-x}$

Funksjonen har større enn 0 hvis

> 0, så er konveks på intervallet . Den er konkav på intervallet .${\ displaystyle f (x) = {\ tfrac {1} {x}}}$${\ displaystyle f '' (x) = {\ tfrac {2} {x^{3}}}}$${\ displaystyle f (x)}$${\ displaystyle (0, \ infty)}$${\ displaystyle (-\ infty, 0)}$

Funksjonen med , er konveks på intervallet og konveks på intervallet , men ikke konveks på intervallet , på grunn av singulariteten ved 

 = 0.${\ displaystyle f (x) = {\ tfrac {1} {x^{2}}}}$${\ displaystyle f (0) = \ infty}$${\ displaystyle (0, \ infty)}$${\ displaystyle (-\ infty, 0)}$${\ displaystyle (-\ infty, \ infty)}$

Funksjoner av n variabler

• LogSumExp -funksjonen, også kalt softmax -funksjon, er en konveks funksjon.
• Funksjonen på domenet til

er konveks.${\ displaystyle -\ log \ det (X)}$

Hver virkelig verdsatt lineær transformasjon er konveks, men ikke strengt konveks, siden hvis f er lineær, da . Denne uttalelsen gjelder også hvis vi erstatter "konveks" med "konkav".${\ displaystyle f (a+b) = f (a)+f (b)}$

Hver virkelig verdsatte affinefunksjon , dvs. hver funksjon i formen , er samtidig konveks og konkav.${\ displaystyle f (x) = a^{T} x+b}$

Hver norm er en konveks funksjon, av trekants ulikhet og positiv homogenitet .

Den spektrale radius av et ikke-negativt matrise er en konveks funksjon av dens diagonale elementer.

Se også

• Konkave funksjon
• Konveks analyse
• Konveks konjugat
• Konveks optimalisering
• Geodesisk konveksitet
• Hermite - Hadamard ulikhet
• Inveks funksjon
• Jensens ulikhet
• K-konveks funksjon
• Kachurovskiis teorem , som relaterer konveksitet til monotonicitet av derivatet
• Karamatas ulikhet
• Logaritmisk konveks funksjon
• Pseudokonveks funksjon
• Kvasikonveks funksjon
• Subderivat av en konveks funksjon

Merknader

Referanser

• Bertsekas, Dimitri (2003). Konveks analyse og optimalisering . Athena Scientific.
• Borwein, Jonathan og Lewis, Adrian. (2000). Konveks analyse og ikke -lineær optimalisering. Springer.
• Donoghue, William F. (1969). Distribusjoner og Fourier -transformasjoner . Academic Press.
• Hiriart-Urruty, Jean-Baptiste og Lemaréchal, Claude . (2004). Grunnleggende om konveks analyse. Berlin: Springer.
• Krasnosel'skii MA , Rutickii Ya.B. (1961). Konvekse funksjoner og Orlicz -mellomrom . Groningen: P.Noordhoff Ltd.
• Lauritzen, Niels (2013). Bachelor konveksitet . World Scientific Publishing.
• Luenberger, David (1984). Lineær og ikke -lineær programmering . Addison-Wesley.
• Luenberger, David (1969). Optimalisering med Vector Space Methods . Wiley & Sons.
• Rockafellar, RT (1970). Konveks analyse . Princeton: Princeton University Press.
• Thomson, Brian (1994). Symmetriske egenskaper for virkelige funksjoner . CRC Press.
• Zălinescu, C. (2002). Konveks analyse i generelle vektorrom . River Edge, NJ: World Scientific Publishing Co., Inc. s. Xx+367. ISBN 981-238-067-1. MR  1921556 .

Eksterne linker

• "Konveks funksjon (av en ekte variabel)" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• "Konveks funksjon (av en kompleks variabel)" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]