Dra kurve - Drag curve
Den dra kurve eller drag polar er forholdet mellom drag på et luftfartøy og andre variabler, slik som heis, koeffisienten for heisen, vinkel angrep eller hastighet. Det kan beskrives med en ligning eller vises som en graf (noen ganger kalt et "polart plot"). Dra kan uttrykkes som faktisk drag eller koeffisienten for dra.
Dra -kurver er nært beslektet med andre kurver som ikke viser drag, for eksempel effektbehov/hastighetskurve eller synkefrekvens/hastighetskurve.
Dra -kurven


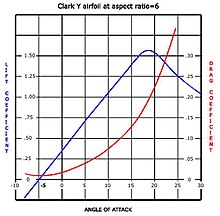
De vesentlige aerodynamiske egenskapene til flyvinger er sammenfattet ved hjelp av to dimensjonsløse størrelser , de løft og drag koeffisienter C, L og C- D . I likhet med andre slike pneumatiske mengder, er de funksjoner bare av angrepsvinkelen α , er Reynolds tall R e og Mach-tallet M . C L og C D kan plottes mot α , eller kan plottes mot hverandre.
Heisen og motstandskreftene, L og D , er skalert med den samme faktor for å få C, L og C D , slik at L / D = C L / C- D . L og D er i rette vinkler, med D parallelt med fri strømhastigheten (den relative hastigheten til den omkringliggende fjerntliggende luften), så den resulterende kraften R ligger i samme vinkel mot D som linjen fra grafens opprinnelse til tilsvarende C L , C D -punkt gjør til C D -aksen.
Hvis en aerodynamisk overflate holdes i en fast angrepsvinkel i en vindtunnel , og størrelsen og retningen til den resulterende kraften måles, kan de plottes ved hjelp av polare koordinater . Når denne målingen gjentas i forskjellige angrepsvinkler, oppnås dragkurven. Løfte- og dra -data ble samlet på denne måten på 1880 -tallet av Otto Lilienthal og rundt 1910 av Gustav Eiffel , men ikke presentert når det gjelder de nyere koeffisientene. Eiffel var den første som brukte navnet "dra polar", men dra kurver er sjelden plottet i dag ved bruk av polare koordinater.
Avhengig av flytypen kan det være nødvendig å plotte dragkurver ved forskjellige Reynolds- og Mach -numre. Utformingen av en fighter vil kreve dragkurver for forskjellige Mach -numre, mens seilfly, som bruker tiden sin på å fly sakte i termisk eller raskt mellom dem, kan kreve kurver ved forskjellige Reynolds -tall, men er upåvirket av komprimerbarhetseffekter. Under utviklingen av designet vil dragkurven bli forbedret. Et bestemt fly kan ha forskjellige kurver selv ved de samme R e- og M -verdiene, for eksempel avhengig av om undervogn og klaffer er utplassert.
Det medfølgende diagrammet viser C L mot C D for et typisk lettfly . Det minste C D- punktet er til venstre mest på plottet. En komponent i drag er indusert drag (en uunngåelig bivirkning av å produsere løft, som kan reduseres ved å øke den angitte lufthastigheten ). Dette er proporsjonalt med C L 2 . De andre dra-mekanismene, parasittisk og bølgedrag , har begge konstante komponenter, totalt C D0 , og løfteavhengige bidrag som øker proporsjonalt med C L 2 . Totalt, da
- C D = C D0 + K. ( C L - C L0 ) 2 .
Effekten av C L0 er å forskyve kurven oppover grafen; fysisk er dette forårsaket av litt vertikal asymmetri, for eksempel en kamret vinge eller en begrenset forekomstvinkel , som sikrer at den minimale dragholdningen gir løft og øker det maksimale løfte -til -drag -forholdet.
Strømbehovskurver
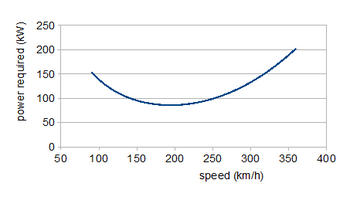
Et eksempel på hvordan kurven brukes i designprosessen er beregningen av den nødvendige effektkurven ( P R ), som viser kraften som trengs for jevn, jevn flyging over driftshastighetsområdet. De involverte kreftene hentes fra koeffisientene ved multiplikasjon med (ρ/2). S V 2 , hvor ρ er tettheten til atmosfæren i flyhøyden, S er vingområdet og V er hastigheten. I nivåflyging er løft lik vekt W og skyvekraft er lik drag, så
- W = (ρ/2) .S. V 2 . C L og
- P R = (ρ/2η) .S. V 3 . C- D .
Ekstrafaktoren til V /η, med η propellens effektivitet , går inn i den andre ligningen fordi P R = (nødvendig skyvekraft) × V /η. Kraft fremfor skyvekraft er passende for et propelldrevet fly, siden det er omtrent uavhengig av hastighet; jetmotorer produserer konstant kraft. Da vekten er konstant, den første av disse ligninger bestemmer hvor C- L faller med økende hastighet. Ved å sette disse C L -verdiene inn i den andre ligningen med C D fra dra -kurven produseres effektkurven. Lavhastighetsregionen viser et fall i løftindusert drag, gjennom et minimum etterfulgt av en økning i profilmotstanden ved høyere hastigheter. Minimumseffekten som kreves, ved en hastighet på 195 km/t (121 mph) er ca 86 kW (115 hk); 135 kW (181 hk) kreves for en maksimal hastighet på 300 km/t (186 mph). Flyvning på kraftminimum vil gi maksimal utholdenhet; hastigheten for størst rekkevidde er der tangenten til effektkurven passerer gjennom opprinnelsen, omtrent 240 km/t (150 mph).)
Hvis et analytisk uttrykk for kurven er tilgjengelig, kan nyttige relasjoner utvikles ved differensiering . For eksempel skjemaet ovenfor, noe forenklet ved å sette C L0 = 0, har en maksimal C L / C D ved C- L 2 = C D0 / K . For et propellfly er dette maksimal utholdenhetstilstand og gir en hastighet på 185 km/t (115 mph). Tilsvarende maksimal rekkevidde er maksimum på C L 3/2 / C D , ved C L 2 = 3.C D0 /K , og derfor er den optimale hastigheten 244 km /t (152 mph). Virkningene av tilnærmingen C L0 = 0 er mindre enn 5%; Selvfølgelig, med en begrenset C L0 = 0,1, gir de analytiske og grafiske metodene de samme resultatene.
Lavhastighetsregionen for flyging er kjent som "baksiden av kraftkurven" (noen ganger "baksiden av dragkurven") der det kreves mer kraft for å fly langsommere. Det er et ineffektivt flyområde fordi hastigheten kan økes og kraften reduseres; det er ingen avveining mellom økt hastighet og økt strømforbruk.
Klatrehastighet
For at et fly skal klatre i en vinkel θ og med hastighet V , må motoren utvikle mer kraft P utover den nødvendige kraften P R for å balansere motstanden som oppleves ved den hastigheten i nivåflyging og vist på plottet med nødvendig effekt. I nivåflyging P R / V = D, men i klatringen er det ekstra vektkomponent som skal inkluderes, det vil si
- P / V = D + W. Sink θ = P R / V + W. Sink θ .
Derav klatre hastighet RC = V .sin θ = ( P - P R ) / W . Forutsatt at motoren på 135 kW som kreves for maksimal hastighet ved 300 km/t er montert, er maksimal overskytende effekt 135 - 87 = 48 Kw ved minimum P R og stigningshastigheten 2,4 m/s.
Seilfly
Uten strøm har et glidfly bare tyngdekraften for å drive det. I en glidevinkel på θ har vekten to komponenter, W. Cos θ i rette vinkler mot flylinjen og W. Synde θ parallelt med den. Disse balanseres av henholdsvis kraft- og løftekomponentene
- W .cos θ = (ρ/2) .S. V 2 . C L og
- W . sin θ = (ρ/2) .S. V 2 . C- D .
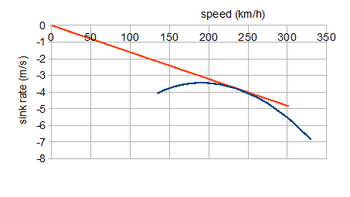
Oppdeling av en ligning av de andre viser at glidevinkelen er gitt ved tan θ = C D / C- L . Egenskapene til mest interesse i strømløs flygingen, er hastigheten over bakken, V g si, og vasken hastighet V s ; disse vises ved å plotte V. sin θ = V s mot V. cos θ = V g . Slike tomter kalles generelt polarer, og for å produsere dem er glidevinkelen som en funksjon av V nødvendig.
En måte å finne løsninger på de to kraftligningene er å kvadrere dem begge og deretter legge sammen; dette viser de mulige C L , C D verdiene ligger på en sirkel med radius 2. W / S .ρ. V 2 . Når dette er avbildet på slepepolaren, finner skjæringspunktet mellom de to kurvene løsningen og dens θ -verdi avleses. Alternativt, med tanke på at glider vanligvis er grunne, kan tilnærmingen cos θ ≃ 1, god for θ mindre enn 10 °, brukes i heisligningen og verdien av C L for en valgt V beregnet, og finne C L fra dra polar og deretter beregne θ.
Eksemplet polar viser her den glidende ytelsen til flyet som er analysert ovenfor, forutsatt at dragpolaren ikke er mye endret av den stasjonære propellen. En rett linje fra opprinnelsen til et punkt på kurven har en gradient som er lik glidevinkelen ved den hastigheten, så den tilsvarende tangenten viser den beste glidevinkelen tan −1 ( C D / C L ) min ≃ 3,3 °. Dette er ikke den laveste vaskehastigheten, men gir den største rekkevidden, som krever en hastighet på 240 km/t (149 mph); minimum synkehastighet på omtrent 3,5 m/s er 180 km/t (112 mph), hastigheter sett i de tidligere, drevne tomtene.
Vaskemengde
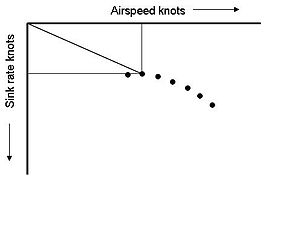
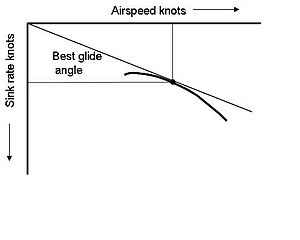
En graf som viser sinkhastigheten til et fly (vanligvis et seilfly ) mot lufthastigheten er kjent som en polarkurve. Polare kurver brukes til å beregne gliderens minimale synkehastighet, beste løft over drag (L/D) og hastighet for å fly .
Polarkurven til en seilfly er avledet fra teoretiske beregninger, eller ved å måle synkehastigheten ved forskjellige lufthastigheter. Disse datapunktene blir deretter forbundet med en linje for å danne kurven. Hver type seilfly har en unik polarkurve, og individuelle seilfly varierer noe avhengig av vingens glatthet, kontrolloverflatemotstand eller tilstedeværelsen av insekter, skitt og regn på vingen. Ulike seilflykonfigurasjoner vil ha forskjellige polarkurver, for eksempel solo versus dual flight, med og uten vannballast, forskjellige klaffinnstillinger, eller med og uten vingespissforlengelser.
Å vite den beste hastigheten å fly er viktig for å utnytte ytelsen til en seilfly. To av de viktigste målene for en seilers ytelse er minimum synkehastighet og beste glideforhold , også kjent som den beste "glidevinkelen". Disse forekommer i forskjellige hastigheter. Å kjenne disse hastighetene er viktig for effektiv langrennsflyging . I stille luft viser polarkurven at flyging med minimum synkehastighet gjør at piloten kan holde seg i luften så lenge som mulig og klatre så raskt som mulig, men med denne hastigheten vil glideren ikke reise så langt som om den fløy på hastighet for beste glid.
Effekt av vind, løft/vask og vekt på beste glidehastighet
Den beste hastigheten for å fly i motvind bestemmes ut fra grafen ved å flytte opprinnelsen til høyre langs den horisontale aksen med motvindens hastighet, og tegne en ny tangentlinje. Denne nye lufthastigheten vil være raskere etter hvert som motvinden øker, men vil resultere i den største tilbakelagte distansen. En generell tommelfingerregel er å legge halvparten av motvindskomponenten til den beste L/D for maksimal avstand. For en medvind forskyves opprinnelsen til venstre av hastigheten på medvinden, og tegner en ny tangentlinje. Medvindens hastighet for å fly vil ligge mellom minimum synke og beste L/D.
I avtagende luft forskyves polarkurven lavere etter luftmassens synkehastighet, og en ny tangentlinje tegnes. Dette vil vise behovet for å fly raskere i senkende luft, noe som gir den nedsenkende luften mindre tid til å senke gliderens høyde. Tilsvarende forskyves polarkurven oppover i henhold til løftehastigheten, og en ny tangentlinje tegnes.
Økt vekt påvirker ikke maksimal rekkevidde for et glidfly. Glidevinkel bestemmes bare av løfte/dra -forholdet. Økt vekt vil kreve økt lufthastighet for å opprettholde den optimale glidevinkelen, så et tyngre glidfly vil ha redusert utholdenhet, fordi det synker langs den optimale glidebanen med en raskere hastighet.
Se også
Eksterne linker
- Glider Performance Airspeeds En animert forklaring på den grunnleggende polarkurven, med modifikasjoner for synkende eller stigende luft og for mot- eller medvind.