Rindler koordinater - Rindler coordinates

I relativistisk fysikk utgjør koordinatene til en hyperbolsk akselerert referanseramme et viktig og nyttig koordinatdiagram som representerer en del av flat Minkowski -romtid . I spesiell relativitet gjennomgår en jevnt akselerert partikkel hyperbolsk bevegelse , for hvilken en jevnt akselerert referanseramme der den er i ro kan velges som sin riktige referanseramme . Fenomenene i denne hyperbolsk akselererte rammen kan sammenlignes med effekter som oppstår i et homogent gravitasjonsfelt . For generell oversikt over akselerasjoner i flat romtid, se Akselerasjon (spesiell relativitet) og Riktig referanseramme (flat romtid) .

I denne artikkelen er lysets hastighet definert av c = 1 , treghetskoordinatene er ( X , Y , Z , T ) , og de hyperboliske koordinatene er ( x , y , z , t ) . Disse hyperbolske koordinatene kan skilles i to hovedvarianter avhengig av den akselererte observatørens posisjon: Hvis observatøren befinner seg på tidspunktet T = 0 i posisjon X = 1/α (med α som den konstante riktige akselerasjonen målt med et akselerometer som kommer ) de hyperboliske koordinatene kalles ofte Rindler -koordinater med den tilsvarende Rindler -metrikken . Hvis observatøren befinner seg på tidspunktet T = 0 i posisjon X = 0 , kalles de hyperbolske koordinatene noen ganger Møller -koordinater eller Kottler – Møller -koordinater med den tilsvarende Kottler – Møller -metrikken . Et alternativt diagram som ofte er relatert til observatører i hyperbolsk bevegelse, oppnås ved hjelp av radarkoordinater som noen ganger kalles Lass -koordinater . Både Kottler – Møller -koordinatene så vel som Lass -koordinatene er også betegnet som Rindler -koordinater.

Når det gjelder historien, ble slike koordinater introdusert like etter ankomsten av spesiell relativitet, da de ble studert (helt eller delvis) sammen med begrepet hyperbolsk bevegelse: I forhold til flat Minkowski romtid av Albert Einstein (1907, 1912), Max Born ( 1909), Arnold Sommerfeld (1910), Max von Laue (1911), Hendrik Lorentz (1913), Friedrich Kottler (1914), Wolfgang Pauli (1921), Karl Bollert (1922), Stjepan Mohorovičić (1922), Georges Lemaître (1924) ), Einstein & Nathan Rosen (1935), Christian Møller (1943, 1952), Fritz Rohrlich (1963), Harry Lass (1963), og i forhold til både flat og buet romtid av generell relativitet av Wolfgang Rindler (1960, 1966) . For detaljer og kilder, se § Historie .

Kjennetegn ved Rindler -rammen

Rindler -diagram, for i ligning ( 1a ), plottet på et Minkowski -diagram. De stiplede linjene er Rindler -horisontene${\ displaystyle \ alpha = 0.5}$

Den World av et legeme i hyperbolsk bevegelse med konstant akselerasjon riktig i -retningen som en funksjon av riktig tid og hurtighet kan gis av ${\ displaystyle \ alpha}$${\ displaystyle X}$ ${\ displaystyle \ tau}$ ${\ displaystyle \ alpha \ tau}$

${\ displaystyle T = x \ sinh (\ alpha \ tau), \ quad X = x \ cosh (\ alpha \ tau)}$

hvor er konstant og er variabel, med verdenslinjen som ligner hyperbola . Sommerfeld viste at ligningene kan tolkes på nytt ved å definere dem som variable og som konstante, slik at den representerer den samtidige "hvileformen" til et legeme i hyperbolsk bevegelse målt av en seende observatør. Ved å bruke observatørens riktige tid som tiden for hele den hyperbolsk akselererte rammen ved innstilling , blir transformasjonsformlene mellom treghetskoordinatene og de hyperboliske koordinatene følgelig: ${\ displaystyle x = 1/\ alpha}$${\ displaystyle \ alpha \ tau}$${\ displaystyle X^{2} -T^{2} = x^{2}}$${\ displaystyle x}$${\ displaystyle \ alpha \ tau}$${\ displaystyle \ tau = t}$

${\ displaystyle T = x \ sinh (\ alpha t), \ quad X = x \ cosh (\ alpha t), \ quad Y = y, \ quad Z = z}$

( 1a )

med det inverse

${\ displaystyle t = {\ frac {1} {\ alpha}} \ operatorname {artanh} \ left ({\ frac {T} {X}} \ right), \ quad x = {\ sqrt {X^{2 } -T^{2}}}, \ quad y = Y, \ quad z = Z}$

Differensiert og satt inn i Minkowski -metrikken , følger beregningen i den hyperbolsk akselererte rammen ${\ displaystyle ds^{2} =-dT^{2}+dX^{2}+dY^{2}+dZ^{2}}$

${\ displaystyle ds^{2} =-(\ alpha x)^{2} dt^{2}+dx^{2}+dy^{2}+dz^{2}}$

( 1b )

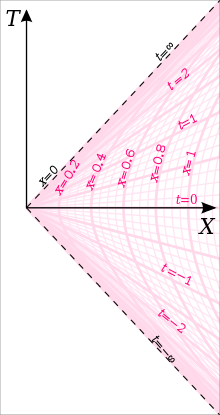
Disse transformasjonene definerer Rindler -observatøren som en observatør som er "i ro" i Rindler -koordinater, dvs. opprettholder konstant x , y , z og bare varierende t etter hvert som tiden går. Koordinatene er gyldige i regionen , som ofte kalles Rindler -kilen , hvis den representerer riktig akselerasjon (langs hyperbola ) til Rindler -observatøren hvis rette tid er definert til å være lik Rindler -koordinattid. For å opprettholde denne verdenslinjen må observatøren akselerere med en konstant riktig akselerasjon, med Rindler -observatører nærmere ( Rindler -horisonten ) som har større riktig akselerasjon. Alle Rindler -observatørene hviler øyeblikkelig i treghetsrammen, og på dette tidspunktet vil en Rindler -observatør med riktig akselerasjon være i posisjon (egentlig , men vi antar enheter hvor ), som også er observatørens konstante avstand fra Rindler -horisonten i Rindler -koordinater. Hvis alle Rindler -observatører setter sine klokker til null på , så når vi definerer et Rindler -koordinatsystem, har vi et valg om hvilken Rindler -observatørs riktige tid vil være lik koordinattiden i Rindler -koordinater, og denne observatørens riktige akselerasjon definerer verdien av ovennevnte ( for andre Rindler -observatører på forskjellige avstander fra Rindler -horisonten, vil koordinattiden være lik et konstant multiplum av sin egen riktige tid). Det er en vanlig konvensjon å definere Rindler -koordinatsystemet slik at Rindler -observatøren hvis rette tid matcher koordinattid er den som har riktig akselerasjon , slik at den kan elimineres fra ligningene. ${\ displaystyle 0 <X <\ infty, \;-X <T <X}$${\ displaystyle \ alpha}$${\ displaystyle x = 1/\ alpha}$${\ displaystyle x = 0}$${\ displaystyle T = 0}$${\ displaystyle \ alpha _ {i}}$${\ displaystyle X = 1/\ alpha _ {i}}$${\ displaystyle X = c^{2}/\ alpha _ {i}}$${\ displaystyle c = 1}$${\ displaystyle T = 0}$${\ displaystyle t}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha = 1}$${\ displaystyle \ alpha}$

Ovenstående ligning er forenklet for . Den uforenklede ligningen er mer praktisk for å finne Rindler Horizon -avstanden, gitt en akselerasjon . ${\ displaystyle c = 1}$${\ displaystyle \ alpha}$

${\ displaystyle {\ begin {align} t & = {\ frac {c} {\ alpha}} \ operatorname {artanh} \ left ({\ frac {cT} {X}} \ right) \; {\ oversett {X \, \ gg \, cT} {\ approx}} \; {\ frac {c^{2} T} {\ alpha X}} \\ X & \ approx {\ frac {c^{2} T} {\ alfa t}} \; {\ oversett {T \, \ approx \, t} {\ approx}} \; {\ frac {c^{2}} {\ alpha}} \ end {align}}}$

Resten av artikkelen vil følge konvensjonen om å sette både og , så enheter for og vil være 1 enhet . Vær oppmerksom på at innstilling av lys-sekund/sekund ² er veldig forskjellig fra å sette lysår/år ² . Selv om vi velger enheter hvor , vil størrelsen på riktig akselerasjon avhenge av vårt valg av enheter: for eksempel hvis vi bruker enheter av lysår for avstand, ( eller ) og år for tid, ( eller ), ville dette bety lysår/år ² , lik 9,5 meter/sekund ² , mens hvis vi bruker lyssekunder for avstand, ( eller ), og sekunder for tid, ( eller ), ville dette bety lys-sekund/sekund ² , eller 299 792 458 meter/sekund ² ). ${\ displaystyle \ alpha = 1}$${\ displaystyle c = 1}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle = c^{2}/\ alpha = 1}$${\ displaystyle \ alpha = 1}$${\ displaystyle \ alpha = 1}$${\ displaystyle c = 1}$${\ displaystyle \ alpha}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle T}$${\ displaystyle t}$${\ displaystyle \ alpha = 1}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle T}$${\ displaystyle t}$${\ displaystyle \ alpha = 1}$

Varianter av transformasjonsformler

En mer generell avledning av transformasjonsformlene gis når den tilsvarende Fermi - Walker tetrad er formulert som Fermi -koordinatene eller riktige koordinatene kan utledes fra. Avhengig av valg av opprinnelse for disse koordinatene, kan man utlede metrikk, tidsutvidelse mellom tiden ved opprinnelsen og på punktet og koordinaten for lyshastigheten (denne variable lyshastigheten motsier ikke spesiell relativitet, fordi den bare er en artefakt av de akselererte koordinatene som brukes, mens den i treghetskoordinater forblir konstant). I stedet for Fermi -koordinater kan også radarkoordinater brukes, som oppnås ved å bestemme avstanden ved hjelp av lyssignaler (se avsnitt Forestillinger om avstand ), der metrikk, tidsutvidelse og lyshastighet ikke lenger er avhengig av koordinatene - spesielt , lysets koordinathastighet forblir identisk med lysets hastighet i treghetsrammer: ${\ displaystyle dt_ {0}}$${\ displaystyle dt}$${\ displaystyle x}$${\ displaystyle | dx |/| dt |}$${\ displaystyle (c = 1)}$

${\ displaystyle X}$ på ${\ displaystyle T = 0}$	Transformasjon, metrisk, tidsutvidelse og koordinat av lysets hastighet
${\ displaystyle X = 0}$	Kottler-Møller koordinerer
	${\ displaystyle {\ begin {array} {c | c} {\ begin {align} T & = \ left (x+{\ frac {1} {\ alpha}} \ right) \ sinh (\ alpha t) \\ X & = \ venstre (x+{\ frac {1} {\ alpha}} \ right) \ cosh (\ alpha t)-{\ frac {1} {\ alpha}} \\ Y & = y \\ Z & = z \ end {align}} og {\ begin {align} t & = {\ frac {1} {\ alpha}} \ operatorname {artanh} \ left ({\ frac {T} {X+{\ frac {1} {\ alpha} }}} \ høyre) \\ x & = {\ sqrt {\ venstre (X+{\ frac {1} {\ alpha}} \ høyre)^{2} -T^{2}}}-{\ frac {1 } {\ alpha}} \\ y & = Y \\ z & = Z \ end {align}} \ end {array}}}$ ( 2a ) ${\ displaystyle ds^{2} =-(1+ \ alpha x) {}^{2} dt^{2}+dx^{2}+dy^{2}+dz^{2}}$ ( 2b ) ${\ displaystyle dt = (1+ \ alpha x) dt_ {0}, \ qquad {\ frac {| dx |} {| dt |}} = 1+ \ alpha x}$ ( 2c )
	Rindler koordinater
${\ displaystyle X = {\ frac {1} {\ alpha}}}$	${\ displaystyle {\ begin {array} {c | c} {\ begin {align} T & = x \ sinh (\ alpha t) \\ X & = x \ cosh (\ alpha t) \\ Y & = y \\ Z & = z \ end {align}} & {\ begin {align} t & = {\ frac {1} {\ alpha}} \ operatorname {artanh} {\ frac {T} {X}} \\ x & = {\ sqrt {X^{2} -T^{2}}} \\ y & = Y \\ z & = Z \ end {align}} \ end {array}}}$ ( 2d ) ${\ displaystyle ds^{2} =-(\ alpha x)^{2} dt^{2}+dx^{2}+dy^{2}+dz^{2}}$ ( 2e ) ${\ displaystyle dt = \ alpha x \ dt_ {0}, \ qquad {\ frac {| dx |} {| dt |}} = \ alpha x}$ ( 2f )
	Radarkoordinater (Lass -koordinater)
${\ displaystyle X = {\ frac {1} {\ alpha}}}$	${\ displaystyle {\ begin {array} {c | c} {\ begin {align} T & = {\ frac {1} {\ alpha}} e^{\ alpha x} \ sinh (\ alpha t) \\ X & = {\ frac {1} {\ alpha}} e^{\ alpha x} \ cosh (\ alpha t) \\ Y & = y \\ Z & = z \ end {align}} & {\ begin {align} t & = {\ frac {1} {\ alpha}} \ operatorname {artanh} {\ frac {T} {X}} \\ x & = {\ frac {1} {2 \ alpha}} \ ln \ venstre [\ alpha {}^{2} \ venstre (X^{2} -T^{2} \ høyre) \ høyre] \\ y & = Y \\ z & = Z \ end {align}} \ end {array}}}$ ( 2g )
	${\ displaystyle ds^{2} = e^{2 \ alpha x} \ left (-dt^{2}+dx^{2} \ right)+dy^{2}+dz^{2}}$ ( 2t ) ${\ displaystyle dt = e^{\ alpha x} dt_ {0}, \ qquad {\ frac {| dx |} {| dt |}} = 1}$ ( 2i )

Rindler -observatørene

I det nye diagrammet ( 1a ) med og er det naturlig å ta coframe -feltet ${\ displaystyle c = 1}$${\ displaystyle \ alpha = 1}$

${\ displaystyle d \ sigma ^{0} = x \, dt, \; \; d \ sigma ^{1} = dx, \; \; d \ sigma ^{2} = dy, \; \; d \ sigma ^{3} = dz}$

som har den doble rammefeltet

${\ displaystyle {\ vec {e}} _ {0} = {\ frac {1} {x}} \ partiell _ {t}, \; \; {\ vec {e}} _ {1} = \ partiell _ {x}, \; \; {\ vec {e}} _ {2} = \ partiell _ {y}, \; \; {\ vec {e}} _ {3} = \ delvis _ {z} }$

Dette definerer en lokal Lorentz -ramme i tangensrommet ved hver hendelse (i regionen som dekkes av vårt Rindler -diagram, nemlig Rindler -kilen). De integrerte kurvene til det tidslignende enhetsvektorfeltet gir en tidaktig kongruens , som består av verdenslinjene til en observatørfamilie kalt Rindler -observatører . I Rindler -diagrammet vises disse verdenslinjene som de vertikale koordinatlinjene . Ved å bruke koordinattransformasjonen ovenfor finner vi at disse tilsvarer hyperboliske buer i det originale kartesiske diagrammet. ${\ displaystyle {\ vec {e}} _ {0}}$${\ displaystyle x = x_ {0}, \; y = y_ {0}, \; z = z_ {0}}$

Noen representative Rindler -observatører (marineblå hyperbolske buer) avbildet ved bruk av det kartesiske diagrammet. De røde linjene 45 grader fra vertikalen representerer Rindler -horisonten; Rindler -koordinatsystemet er bare definert til høyre for denne grensen.

Som med enhver tidlignende kongruens i enhver Lorentzian -manifold, har denne kongruensen en kinematisk dekomponering (se Raychaudhuri -ligningen ). I dette tilfellet forsvinner ekspansjonen og vortisiteten til kongruensen til Rindler -observatører . Forsvinningen av ekspansjonstensoren innebærer at hver av våre observatører holder konstant avstand til sine naboer . Forsvinningen av vortex -tensoren innebærer at observatørens verdenslinjer ikke vrir seg om hverandre; dette er et slags lokalt fravær av "virvling".

Den akselerasjonsvektor for hver observatør er gitt ved den kovariante derivatet

${\ displaystyle \ nabla _ {{\ vec {e}} _ {0}} {\ vec {e}} _ {0} = {\ frac {1} {x}} {\ vec {e}} _ { 1}}$

Det vil si at hver Rindler -observatør akselererer i retningen. Individuelt sett akselererer hver observatør faktisk med konstant størrelse i denne retningen, så deres verdenslinjer er de Lorentziske sirkelanalogene, som er kurvene for konstant kurvatur i den euklidiske geometrien. ${\ displaystyle \ partial _ {x}}$

Fordi Rindler-observatørene er virvelfrie , er de også ortogonale på overflaten . De ortogonale romlige hyperslices er ; disse vises som horisontale halvplan i Rindler-diagrammet og som halvplaner gjennom i det kartesiske diagrammet (se figuren ovenfor). Innstilling i linjen element, ser vi at disse har det vanlige Euklidsk geometri, . Dermed har de romlige koordinatene i Rindler -diagrammet en veldig enkel tolkning som er i samsvar med påstanden om at Rindler -observatørene er gjensidig stasjonære. Vi kommer tilbake til denne stivhetsegenskapen til Rindler -observatørene litt senere i denne artikkelen. ${\ displaystyle t = t_ {0}}$${\ displaystyle T = X = 0}$${\ displaystyle dt = 0}$${\ displaystyle d \ sigma^{2} = dx^{2}+dy^{2}+dz^{2}, \; \ forall x> 0, \ forall y, z}$

En "paradoksal" eiendom

Legg merke til at Rindler -observatører med mindre konstant x -koordinat akselererer vanskeligere for å følge med. Dette kan virke overraskende fordi i Newtonsk fysikk må observatører som holder konstant relativ avstand dele den samme akselerasjonen. Men i relativistisk fysikk ser vi at det sluttende endepunktet til en stang som akselereres av en ekstern kraft (parallelt med symmetriaksen) må akselerere litt hardere enn det ledende endepunktet, ellers må den til slutt bryte. Dette er en manifestasjon av Lorentz sammentrekning . Når stangen akselererer, øker hastigheten og lengden minker. Siden det blir kortere, må bakenden akselerere hardere enn fronten. En annen måte å se på det er: bakenden må oppnå den samme endringen i hastighet på kortere tid. Dette fører til en differensialligning som viser at akselerasjonen til den bakre enden på en eller annen avstand divergerer, noe som resulterer i Rindler -horisonten .

Dette fenomenet er grunnlaget for et velkjent "paradoks", Bells romskipsparadoks . Imidlertid er det en enkel konsekvens av relativistisk kinematikk. En måte å se dette på er å observere at størrelsen på akselerasjonsvektoren bare er kurven på banen til den tilsvarende verdenslinjen. Men verdenslinjene til våre Rindler -observatører er analogene til en familie av konsentriske sirkler i det euklidiske planet, så vi har ganske enkelt å gjøre med den Lorentzian -analogen til et faktum som er kjent for hurtigløpere: i en familie av konsentriske sirkler må indre sirkler bøye seg raskere (per buelengde) enn de ytre .

Minkowski -observatører

En representant Minkowski -observatør (marineblå hyperbolsk sekantkurve) avbildet ved bruk av Rindler -diagrammet. Rindler -horisonten er vist med rødt.

Det er verdt å også introdusere en alternativ ramme, gitt i Minkowski -diagrammet av det naturlige valget

${\ displaystyle {\ vec {f}} _ {0} = \ partiell _ {T}, \; {\ vec {f}} _ {1} = \ delvis _ {X}, \; {\ vec {f }} _ {2} = \ delvis _ {Y}, \; {\ vec {f}} _ {3} = \ delvis _ {Z}}$

Ved å transformere disse vektorfeltene ved hjelp av koordinattransformasjonen gitt ovenfor, finner vi at i Rindler -diagrammet (i Rinder -kilen) blir denne rammen

${\ displaystyle {\ begynne {justert} {\ vec {f}} _ {0} & = {\ frac {1} {x}} \ cosh (t) \, \ partiell _ {t}-\ sinh (t ) \, \ delvis _ {x} \\ {\ vec {f}} _ {1} & =-{\ frac {1} {x}} \ sinh (t) \, \ delvis _ {t}+\ cosh (t) \, \ partiell _ {x} \\ {\ vec {f}} _ {2} & = \ delvis _ {y}, \; {\ vec {f}} _ {3} = \ delvis _ {z} \ end {align}}}$

Beregning av den kinematiske nedbryting av timelike kongruens definert av timelike enhetsvektor-feltet , finner vi at ekspansjonen og virvlingen igjen forsvinner, og i tillegg akselerasjonsvektoren forsvinner, . Med andre ord er dette en geodesisk kongruens ; de tilsvarende observatørene er i en tilstand av treghet . I det originale kartesiske diagrammet hviler disse observatørene, som vi vil kalle Minkowski -observatører . ${\ displaystyle {\ vec {f}} _ {0}}$${\ displaystyle \ nabla _ {{\ vec {f}} _ {0}} {\ vec {f}} _ {0} = 0}$

I Rindler -diagrammet fremstår verdenslinjene til Minkowski -observatørene som hyperbolske sekantkurver asymptotiske for koordinatplanet . Nærmere bestemt, i Rindler koordinater, verdens linjen i Minkowski observatør som passerer gjennom arrangementet er ${\ displaystyle x = 0}$${\ displaystyle t = t_ {0}, \; x = x_ {0}, \; y = y_ {0}, \; z = z_ {0}}$

${\ displaystyle {\ begin {align} t & = \ operatorname {artanh} \ left ({\ frac {s} {x_ {0}}} \ right), \;-x_ {0} <s <x_ {0} \\ x & = {\ sqrt {x_ {0}^{2} -s^{2}}}, \;-x_ {0} <s <x_ {0} \\ y & = y_ {0} \\ z & = z_ {0} \ end {align}}}$

hvor er den riktige tiden for denne Minkowski -observatøren. Vær oppmerksom på at bare en liten del av hans historie er dekket av Rindler -diagrammet. Dette viser eksplisitt hvorfor Rindler -diagrammet ikke er geodesisk komplett ; tidlignende geodesikk løper utenfor regionen som dekkes av diagrammet i endelig god tid. Selvfølgelig visste vi allerede at Rindler -diagrammet ikke kan være geodesisk komplett, fordi det bare dekker en del av det originale kartesiske diagrammet, som er et geodesisk komplett diagram. ${\ displaystyle s}$

I tilfellet avbildet i figuren, og vi har tegnet (riktig skalert og forsterket) lyskeglene på . ${\ displaystyle x_ {0} = 1}$${\ displaystyle s \ in \ left \ {-{\ frac {1} {2}}, \; 0, \; {\ frac {1} {2}} \ right \}}$

Rindler -horisonten

Rindler -koordinatdiagrammet har en koordinatsingularitet ved x  = 0, hvor den metriske tensoren (uttrykt i Rindler -koordinatene) har forsvinnende determinant . Dette skjer fordi x x  0 akselerasjonen til Rindler -observatørene avviker. Som vi kan se fra figuren som illustrerer Rindler-kilen, tilsvarer locus x  = 0 i Rindler-diagrammet locus T ²  =  X ² ,  X  > 0 i det kartesiske diagrammet, som består av to null halvplaner, hver styrt ved en null geodetisk kongruens.

For øyeblikket anser vi ganske enkelt Rindler -horisonten som grensen for Rindler -koordinatene. Hvis vi ser på settet med akselererende observatører som har en konstant posisjon i Rindler -koordinater, kan ingen av dem noen gang motta lyssignaler fra hendelser med T  ≥  X (på diagrammet vil dette være hendelser på eller til venstre for linjen T = X som den øvre røde horisonten ligger langs; disse observatørene kunne imidlertid motta signaler fra hendelser med T  ≥  X hvis de stoppet akselerasjonen og krysset denne linjen selv) eller kunne noen gang ha sendt signaler til hendelser med T  ≤ - X (hendelser på eller til venstre for linjen T = - X som den nedre røde horisonten ligger langs, disse hendelsene ligger utenfor alle fremtidige lyskjegler på deres tidligere verdenslinje). Hvis vi også betrakter medlemmer av dette settet med akselererende observatører nærmere og nærmere horisonten, i grensen når avstanden til horisonten nærmer seg null, vil den konstante akselerasjonen som en observatør opplever på denne avstanden (som også ville være G- kraft som en slik observatør opplever) ville nærme seg uendelig. Begge disse fakta ville også være sanne hvis vi vurderte et sett med observatører som svever utenfor hendelseshorisonten til et svart hull , hver observatør svever i en konstant radius i Schwarzschild -koordinatene . Faktisk, i det nære nabolaget til et svart hull, kan geometrien nær hendelseshorisonten beskrives i Rindler -koordinater. Hawking -stråling i tilfelle en akselererende ramme kalles Unruh -stråling . Tilkoblingen er ekvivalensen mellom akselerasjon og gravitasjon.

Geodesikk

De geodesiske ligningene i Rindler -diagrammet er lett å få fra den geodesiske Lagrangian ; de er

${\ displaystyle {\ ddot {t}}+{\ frac {2} {x}} \, {\ dot {x}} \, {\ dot {t}} = 0, \; {\ ddot {x} }+x \, {\ dot {t}}^{2} = 0, \; {\ ddot {y}} = 0, \; {\ ddot {z}} = 0}$

Selvfølgelig, i det originale kartesiske diagrammet, vises geodesikkene som rette linjer, så vi kan enkelt få dem i Rindler -diagrammet ved å bruke vår koordinattransformasjon. Det er imidlertid lærerikt å skaffe og studere dem uavhengig av det opprinnelige diagrammet, og vi skal gjøre det i denne delen.

Noen representative nullgeodesikk (svarte hyperbolske halvcirkelbuer) projisert inn i den romlige hyperslice t  = 0 til Rindler -observatørene. Rindler -horisonten vises som et magentaplan.

Fra den første, tredje og fjerde får vi umiddelbart de første integralene

${\ displaystyle {\ dot {t}} = {\ frac {E} {x^{2}}}, \; \; {\ dot {y}} = P, \; \; {\ dot {z} } = Q}$

Men fra linjeelementet har vi hvor for henholdsvis tidlignende, null og romlignende geodesikk. Dette gir den fjerde første integralen, nemlig ${\ displaystyle \ varepsilon = -x^{2} \, {\ dot {t}}^{2}+{\ dot {x}}^{2}+{\ dot {y}}^{2}+ {\ dot {z}}^{2}}$${\ displaystyle \ varepsilon \ in \ left \ {-1, \, 0, \, 1 \ right \}}$

${\ displaystyle {\ dot {x}}^{2} = \ left (\ varepsilon +{\ frac {E^{2}} {x^{2}}} \ right) -P^{2} -Q ^{2}}$.

Dette er nok til å gi den komplette løsningen av de geodesiske ligningene.

Når det gjelder null geodesikk , fra med null , ser vi at x -koordinaten varierer over intervallet . ${\ displaystyle {\ frac {E^{2}} {x^{2}}} \,-\, P^{2} \,-\, Q^{2}}$${\ displaystyle E}$${\ displaystyle 0 \, <\, x \, <\, {\ frac {E} {\ sqrt {P^{2} \,+\, Q^{2}}}}}}$

Den komplette syv parameterfamilien som gir enhver null geodesikk gjennom enhver hendelse i Rindler -kilen, er

${\ displaystyle {\ begin {align} t-t_ {0} & = \ operatorname {artanh} \ left ({\ frac {1} {E}} \ left [s \ left (P^{2}+Q^ {2} \ høyre)-{\ sqrt {E^{2}-\ venstre (P^{2}+Q^{2} \ høyre) x_ {0}^{2}}} \ høyre] \ høyre) +\\ & \ qquad \ operatorname {artanh} \ left ({\ frac {1} {E}} {\ sqrt {E^{2}-(P^{2}+Q^{2}) x_ {0 }^{2}}} \ høyre) \\ x & = {\ sqrt {x_ {0}^{2}+2s {\ sqrt {E^{2}-(P^{2}+Q^{2} ) x_ {0}^{2}}}-s^{2} (P^{2}+Q^{2})}} \\ y-y_ {0} & = Ps; \; \; z- z_ {0} = Spørsmål \ slutt {justert}}}$

Ved å plotte sporene til noen representative null -geodesikk gjennom en gitt hendelse (det vil si projisere til hyperslisen ), får vi et bilde som mistenkelig ligner familien til alle halvsirkler gjennom et punkt og ortogonal til Rindler -horisonten (se figuren). ${\ displaystyle t = 0}$

Fermat -metrikk

Det faktum at i Rindler -diagrammet, projeksjonene av null geodesikk til enhver romlig hyperslice for Rindler -observatørene ganske enkelt er halvsirkelbuer, kan verifiseres direkte fra den generelle løsningen som nettopp er gitt, men det er en veldig enkel måte å se dette på. En statisk romtid er en tid der det finnes et virvelfritt tidlignende Killing-vektorfelt . I dette tilfellet har vi en unik definert familie av (identiske) romlige hyperslices ortogonale med de tilsvarende statiske observatørene (som ikke trenger å være treghetsobservatører). Dette tillater oss å definere en ny beregning på noen av disse hypersliceene som er i samsvar med den opprinnelige metrikken som ble arvet fra romtiden, men med egenskapen som geodesikk i den nye metriken (merk at dette er en Riemannian-beregning på en Riemannian tre-manifold) er nettopp anslagene til null -geodetikken i romtiden. Denne nye metrikken kalles Fermat -metriken , og i en statisk romtid utstyrt med et koordinatdiagram der linjeelementet har formen

${\ displaystyle ds^{2} = g_ {00} \, dt^{2}+g_ {jk} \, dx^{j} \, dx^{k}, \; \; j, \; k \ i \ {1,2,3 \}}$

Fermat -metrikken på er ganske enkelt ${\ displaystyle t = 0}$

${\ displaystyle d \ rho^{2} = {\ frac {1} {-g_ {00}}} \ venstre (g_ {jk} \, dx^{j} \, dx^{k} \ høyre)}$

(der de metriske koeffientene skal vurderes til ). ${\ displaystyle t = 0}$

I Rindler -diagrammet er den tidlignende oversettelsen et slikt drapvektorfelt, så dette er en statisk romtid (ikke overraskende, siden Minkowski romtid selvfølgelig er trivielt en statisk vakuumløsning av Einstein -feltligningen ). Derfor kan vi umiddelbart skrive ned Fermat -metrikken for Rindler -observatørene: ${\ displaystyle \ delvis _ {t}}$

${\ displaystyle d \ rho^{2} = {\ frac {1} {x^{2}}} \ venstre (dx^{2}+dy^{2}+dz^{2} \ høyre), \ ; \; \ forall x> 0, \; \; \ forall y, z}$

Men dette er det velkjente linjeelementet i hyperbolsk H- ^trerom i det øvre halve romdiagrammet . Dette er nært analogt med det velkjente diagrammet for det øvre halvplanet for det hyperboliske planet H ² , som er kjent for generasjoner av komplekse analysestudenter i forbindelse med konformale kartleggingsproblemer (og mye mer), og mange matematisk tenkte lesere vet allerede at geodesikken av H- ² i den øvre halvdel planet modell er bare halvsirkler (ortogonale til sirkelen i uendelig representert ved den reelle aksen).

Symmetrier

Siden Rindler -diagrammet er et koordinatdiagram for Minkowski romtid, forventer vi å finne ti lineært uavhengige Killing -vektorfelt. Faktisk, i kartesiske diagrammet kan vi lett finne ti lineært uavhengige Killing vektorfelt, genererer henholdsvis ett parameter undergrupper av tid oversettelses , tre spatials, tre rotasjoner og tre øker. Sammen genererer disse (riktig isokron) Poincaré -gruppen, symmetri -gruppen til Minkowski -romtiden.

Imidlertid er det lærerikt å skrive ned og løse Killing -vektorligningene direkte. Vi får fire kjente utseende Killing -vektorfelt

${\ displaystyle \ partiell _ {t}, \; \; \ delvis _ {y}, \; \; \ delvis _ {z}, \; \;-z \, \ delvis _ {y}+y \, \ delvis _ {z}}$

(tidsoversettelse, romlige oversettelser ortogonale i akselerasjonsretningen og romlig rotasjon ortogonal i akselerasjonsretningen) pluss seks til:

${\ displaystyle {\ begynne {justert} og \ exp (\ pm t) \, \ venstre ({\ frac {y} {x}} \, \ delvis _ {t} \ pm \ venstre [y \, \ delvis _ {x} -x \, \ delvis _ {y} \ høyre] \ høyre) \\ & \ exp (\ pm t) \, \ venstre ({\ frac {z} {x}} \, \ delvis _ {t} \ pm \ venstre [z \, \ delvis _ {x} -x \, \ delvis _ {z} \ høyre] \ høyre) \\ & \ exp (\ pm t) \, \ venstre ({\ frac {1} {x}} \, \ delvis _ {t} \ pm \ delvis _ {x} \ høyre) \ ende {justert}}}$

(der tegnene er valgt konsekvent + eller -). Vi lar det være en øvelse å finne ut hvordan disse er relatert til standardgeneratorene; her ønsker vi å påpeke at vi må være i stand til å skaffe generatorer tilsvarende i det kartesiske diagrammet, men Rindler -kilen er åpenbart ikke invariant under denne oversettelsen. Hvordan kan dette være? Svaret er at i likhet med alt som er definert av et system med partielle differensialligninger på en jevn manifold, vil Killing -ligningen generelt ha lokalt definerte løsninger, men disse eksisterer kanskje ikke globalt. Det vil si at med passende begrensninger på gruppeparameteren kan en Killing-strøm alltid defineres i et egnet lokalt nabolag , men strømmen er kanskje ikke veldefinert globalt . Dette har ingenting å gjøre med Lorentzian -manifolder i seg selv, siden det samme problemet oppstår i studiet av generelle glatte manifolds . ${\ displaystyle \ partial _ {T}}$

Forestillinger om avstand

En av de mange verdifulle lærdommene som kan læres av en studie av Rindler -diagrammet, er at det faktisk er flere distinkte (men rimelige) forestillinger om avstand som kan brukes av Rindler -observatørene.

Operasjonell betydning av radaravstanden mellom to Rindler -observatører (marineblå vertikale linjer). Rindler -horisonten er vist til venstre (rød vertikal linje). Verdenslinjen til radarpulsen er også avbildet, sammen med (riktig skalert) lyskjegler ved hendelser A, B, C.

Den første er den vi stiltiende har brukt ovenfor: den induserte Riemannian -metriken på de romlige hyperslice . Vi vil kalle dette linjalavstanden siden den tilsvarer denne induserte Riemannian -metrikken, men dens operasjonelle betydning er kanskje ikke umiddelbart åpenbar. ${\ displaystyle t = t_ {0}}$

Sett fra fysisk måling er radaravstanden en mer naturlig forestilling om avstand mellom to verdenslinjer . Dette beregnes ved å sende en null geodetikk fra verdenslinjen til vår observatør (hendelse A) til verdenslinjen til et lite objekt, hvorpå den reflekteres (hendelse B) og går tilbake til observatøren (hendelse C). Radaravstanden oppnås deretter ved å dele reisetiden for tur / retur, målt med en ideell klokke båret av observatøren vår.

(I Minkowski romtid, heldigvis, kan vi ignorere muligheten for flere null geodesiske stier mellom to verdenslinjer, men i kosmologiske modeller og andre applikasjoner er ting ikke så enkelt. Vi bør også advare mot å anta at denne forestillingen om avstand mellom to observatører gir en forestilling som er symmetrisk under utveksling av observatørene.)

Spesielt vurdere et par Rindler observatører med koordinater og hhv. (Vær oppmerksom på at den første av disse, den etterfølgende observatøren, akselererer litt hardere for å holde tritt med den ledende observatøren). Når vi setter inn Rindler -linjeelementet, får vi lett likningen av null geodesikk som beveger seg i akselerasjonsretningen: ${\ displaystyle x = x_ {0}, \; y = 0, \; z = 0}$${\ displaystyle x = x_ {0}+h, \; y = 0, \; z = 0}$${\ displaystyle dy = dz = 0}$

${\ displaystyle t-t_ {0} = \ log \ left ({\ frac {x} {x_ {0}}} \ right)}$

Derfor er radaravstanden mellom disse to observatørene gitt av

${\ displaystyle x_ {0} \, \ log \ left (1+{\ frac {h} {x_ {0}}} \ right) = h-{\ frac {h^{2}} {2 \, x_ {0}}}+O \ venstre (h^{3} \ høyre)}$

Dette er litt mindre enn linjalavstanden, men for observatører i nærheten er avviket ubetydelig.

En tredje mulig forestilling om avstand er denne: observatøren vår måler vinkelen som en enhetskive har plassert på et objekt (ikke et punktobjekt), slik den ser ut fra plasseringen hans. Vi kaller dette avstanden for optisk diameter . På grunn av den enkle karakteren av null geodesikk i Minkowski romtid, kan vi lett bestemme den optiske avstanden mellom våre par Rindler -observatører (justert med akselerasjonsretningen). Fra en skisse bør det være sannsynlig at den optiske diameteren avstand skalerer liker . Derfor, i tilfelle av en etterfølgende observatør som estimerer avstand til en ledende observatør (saken ), er den optiske avstanden litt større enn linjalavstanden, som er litt større enn radaravstanden. Leseren bør nå ta et øyeblikk til å vurdere saken om en ledende observatør som estimerer avstand til en etterfølgende observatør. ${\ textstyle h+{\ frac {1} {x_ {0}}}+O \ venstre (h^{3} \ høyre)}$${\ displaystyle h> 0}$

Det er andre forestillinger om avstand, men hovedpoenget er klart: Selv om verdiene til disse forskjellige forestillingene generelt vil være uenige for et gitt par Rindler -observatører, er de alle enige om at hvert par Rindler -observatører holder konstant avstand . Det faktum at svært nærliggende Rindler -observatører er gjensidig stasjonære følger av det faktum som er nevnt ovenfor, at ekspansjonstensoren til Rindler -kongruensen forsvinner identisk. Imidlertid har vi vist her at på forskjellige måter holder denne stivhetsegenskapen på større skalaer. Dette er virkelig en bemerkelsesverdig stivhetsegenskap, gitt det velkjente faktum at i relativistisk fysikk kan ingen stang akselereres stivt (og ingen disk kan spinnes stivt ) -i hvert fall ikke uten å opprettholde inhomogene påkjenninger. Den enkleste måten å se dette på er å observere at i Newtonsk fysikk, hvis vi "sparker" en stiv kropp, vil alle materieelementer i kroppen umiddelbart endre bevegelsestilstanden. Dette er selvfølgelig uforenlig med det relativistiske prinsippet om at ingen informasjon som har noen fysisk effekt kan overføres raskere enn lysets hastighet.

Det følger at hvis en stang akselereres av en ekstern kraft som påføres hvor som helst langs lengden, kan ikke elementene av materie på forskjellige forskjellige steder i stangen alle kjenne den samme størrelsen på akselerasjonen hvis stangen ikke skal strekke seg uten bånd og til slutt bryte. Med andre ord må en akselerert stang som ikke går i stykker, opprettholde påkjenninger som varierer langs dens lengde. Videre i ethvert tankeeksperiment med tidsvarierende krefter, enten vi "sparker" et objekt eller prøver å akselerere det gradvis, kan vi ikke unngå problemet med å unngå mekaniske modeller som er inkonsekvente med relativistisk kinematikk (fordi fjerne deler av kroppen reagerer for raskt til en påført kraft).

Når vi går tilbake til spørsmålet om linjeavstandens operasjonelle betydning, ser vi at dette bør være avstanden våre observatører vil oppnå hvis de veldig sakte går fra hånd til hånd en liten linjal som gjentatte ganger settes ende til ende. Men å begrunne denne tolkningen i detalj ville kreve en slags materiell modell.

Generalisering til buede mellomrom

Rindlerkoordinater som beskrevet ovenfor kan generaliseres til buet romtid, som Fermis normale koordinater . Generaliseringen avgjørende innebærer å konstruere en passende ortonormal tetrad og deretter transportere den langs den gitte banen ved hjelp av Fermi - Walker transportregel . For detaljer, se papiret av Ni og Zimmermann i referansene nedenfor. En slik generalisering gjør det faktisk mulig å studere treghet og gravitasjonseffekter i et jordbasert laboratorium, så vel som de mer interessante koblede treghet-gravitasjonseffektene.

Historie

Oversikt

Kottler – Møller og Rindler koordinater

Albert Einstein (1907) studerte effektene innenfor en jevnt akselerert ramme, og skaffet ligninger for koordinatavhengig tidsutvidelse og lyshastighet tilsvarende ( 2c ), og for å gjøre formlene uavhengige av observatørens opprinnelse, oppnådde han tidsutvidelse ( 2i ) i formell avtale med radarkoordinater. Mens han introduserte begrepet Born rigidity , bemerket Max Born (1909) at formlene for hyperbolsk bevegelse kan brukes som transformasjoner til et "hyperbolisk akselerert referansesystem" ( tysk : hyperbolisch beschleunigtes Bezugsystem ) tilsvarende ( 2d ). Born arbeid ble videre utdypet av Arnold Sommerfeld (1910) og Max von Laue (1911) som begge oppnådde ( 2d ) ved hjelp av imaginære tall, som ble oppsummert av Wolfgang Pauli (1921) som foruten koordinater ( 2d ) også oppnådde metriske ( 2e ) ved hjelp av imaginære tall. Einstein (1912) studerte et statisk gravitasjonsfelt og oppnådde Kottler-Møller-metrikk ( 2b ) samt tilnærminger til formler ( 2a ) ved bruk av en koordinatavhengig lyshastighet. Hendrik Lorentz (1913) oppnådde koordinater som ligner på ( 2d , 2e , 2f ) mens han studerte Einsteins ekvivalensprinsipp og det ensartede gravitasjonsfeltet.

En detaljert beskrivelse ble gitt av Friedrich Kottler (1914), som formulerte den tilsvarende ortonormale tetrad , transformasjonsformler og metriske ( 2a , 2b ). Også Karl Bollert (1922) oppnådde metrikken ( 2b ) i studiet av jevn akselerasjon og jevne gravitasjonsfelt. I en artikkel om Born rigidity oppnådde Georges Lemaître (1924) koordinater og metriske ( 2a , 2b ). Albert Einstein og Nathan Rosen (1935) beskrev ( 2d , 2e ) som de "velkjente" uttrykkene for et homogent gravitasjonsfelt. Etter at Christian Møller (1943) oppnådde ( 2a , 2b ) i som studie relatert til homogene gravitasjonsfelt, brukte han (1952) så vel som Misner & Thorne & Wheeler (1973) Fermi – Walker transport for å få de samme ligningene.

Mens disse undersøkelsene gjaldt flat romtid, analyserte Wolfgang Rindler (1960) hyperbolsk bevegelse i buet romtid, og viste (1966) analogien mellom de hyperboliske koordinatene ( 2d , 2e ) i flat romtid med Kruskal -koordinater i Schwarzschild -rommet . Dette påvirket påfølgende forfattere i deres formulering av Unruh -stråling målt av en observatør i hyperbolsk bevegelse, som ligner beskrivelsen av Hawking -stråling av sorte hull .

Horisont

Born (1909) viste at de indre punktene til en Born stiv kropp i hyperbolsk bevegelse bare kan være i regionen . Sommerfeld (1910) definerte at koordinatene som er tillatt for transformasjonen mellom treghet og hyperboliske koordinater må tilfredsstille . Kottler (1914) definerte denne regionen som og påpekte eksistensen av et "grensefly" ( tysk : Grenzebene ) , utover hvilket intet signal kan nå observatøren i hyperbolsk bevegelse. Dette ble kalt "observatørens horisont" ( tysk : Horizont des Beobachters ) av Bollert (1922). Rindler (1966) demonstrerte forholdet mellom en slik horisont og horisonten i Kruskal -koordinater. ${\ displaystyle X/\ left (X^{2} -T^{2} \ right)> 0}$${\ displaystyle T <X}$${\ displaystyle X^{2} -T^{2}> 0}$${\ displaystyle c^{2}/\ alfa +x}$

Radarkoordinater

Ved å bruke Bollerts formalisme, tok Stjepan Mohorovičić (1922) et annet valg for en parameter og oppnådde metrisk ( 2t ) med en trykkfeil, som ble korrigert av Bollert (1922b) med en annen utskriftsfeil, til en versjon uten utskriftsfeil ble gitt av Mohorovičić (1923). I tillegg hevdet Mohorovičić feilaktig at metrisk ( 2b , nå kalt Kottler-Møller metric) er feil, noe som ble tilbakevist av Bollert (1922). Metrisk ( 2t ) ble gjenoppdaget av Harry Lass (1963), som også ga de tilsvarende koordinatene ( 2g ) som noen ganger kalles "Lass -koordinater". Metrisk ( 2t ), så vel som ( 2a , 2b ), ble også avledet av Fritz Rohrlich (1963). Etter hvert ble Lass -koordinatene ( 2g , 2h ) identifisert med radarkoordinater av Desloge & Philpott (1987).

Tabell med historiske formler

Einstein (1907) ${\ displaystyle {\ scriptstyle {\ begin {matrix} \ sigma = \ tau \ left (1+{\ frac {\ gamma \ xi} {c^{2}}} \ right) \\\ sigma = \ tau e ^{\ gamma \ xi /c^{2}} \\ c \ left (1+{\ frac {\ gamma \ xi} {c^{2}}} \ right) \ end {matrise}}}}}$ Født (1909) ${\ displaystyle {\ scriptstyle {\ begin {matrise} x = -q \ xi, \ y = \ eta, \ z = \ zeta, \ t = {\ frac {p} {c^{2}}} \ xi \\\ venstre (p = x _ {\ tau}, \ q = -t _ {\ tau} = {\ sqrt {1+p^{2}/c^{2}}} \ høyre) \\ {\ boldsymbol {\ downarrow}} \\ x^{2} -c^{2} t^{2} = \ xi^{2} \ end {matrise}}}}$ Herglotz (1909) ${\ displaystyle {\ scriptstyle {\ begin {matrise} {\ begin {align} x & = x '\\ y & = y' \\ tz & = (t'-z ') e^{\ vartheta} \\ t+z & = (t '+z') e^{-\ vartheta} \ end {align}} \\ {\ boldsymbol {\ downarrow}} \\ x = x_ {0}, \ quad y = y_ {0}, \ quad z = {\ sqrt {z_ {0}^{2}+t^{2}}} \ end {matrise}}}}$ Sommerfeld (1910) ${\ displaystyle \ scriptstyle {\ begin {align} x & = r \ cos \ varphi \\ y & = y '\\ z & = z' \\ l & = r \ sin \ varphi \\\ varphi & = i \ psi, \ l = ict \ end {align}}}$ von Laue (1911) ${\ displaystyle \ scriptstyle {\ begin {align} X & = R \ cos \ varphi \\ L & = R \ sin \ varphi \\ R^{2} & = X^{2}+L^{2} \\\ tan \ varphi & = {\ frac {L} {X}} \ end {align}}}$ Einstein (1912) ${\ displaystyle {\ scriptstyle {\ begin {matrix} d \ xi^{2} -d \ tau^{2} = dx^{2} -c^{2} dt^{2} \\ {\ boldsymbol { \ downarrow}} \\ c = c_ {0}+ax \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {align} \ xi & = x+{\ frac {ac} {2}} t^{ 2} \\\ eta & = y \\\ zeta & = z \\\ tau & = ct \ end {align}} \ end {matrix}}}}}$ Kottler (1912) ${\ displaystyle {\ scriptstyle {\ begin {align} x^{(1)} & = x_ {0}^{(1)} \\ x^{(2)} & = x_ {0}^{(2 )} \\ x^{(3)} & = b \ cos i \ varphi \\ x^{(4)} & = b \ sin i \ varphi \ end {justert}}}}}$ Lorentz (1913) ${\ displaystyle {\ scriptstyle {\ begin {matrix} dc = {\ frac {g} {c}} dz \\\ hline {\ begin {align} z & = a \ left (z'-z_ {0}^{ \ prime} \ right) \\ ct & = b \ left (z'-z_ {0}^{\ prime} \ right) \\ a & = {\ frac {1} {2}} \ left (e^{kt '}+e^{-kt} \ right) \\ b & = {\ frac {1} {2}} \ left (e^{kt'}-e^{-kt} \ right) \ end {align} } \\ {\ boldsymbol {\ downarrow}} \\ c '= k \ venstre (z'-z_ {0}^{\ prime} \ høyre), \ z'-z_ {0}^{\ prime} = {\ frac {c^{2}} {g}} \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {align} & dx^{2}+dy^{2}+dz^{2}- c^{2} dt \\ & = dx^{\ prime 2}+dy^{\ prime 2}+dz^{\ prime 2} -c^{\ prime 2} dt^{\ prime 2} \ end {align}} \ end {matrise}}}}$

Kottler (1914a) ${\ displaystyle {\ scriptstyle {\ begin {matrise} {\ begin {justert} x^{(1)} & = x_ {0}^{(1)} \\ x^{(2)} & = x_ { 0}^{(2)} \\ x^{(3)} & = b \ cos iu \\ x^{(4)} & = b \ sin iu \ end {align}} \\ {\ boldsymbol { \ downarrow}} \\ ds^{2} =-c^{2} d \ tau^{2} = b^{2} (du)^{2} \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {matrise} c_ {1}^{(1)} = 0, && c_ {1}^{(2)} = 0, && c_ {1}^{(3)} =-\ sin iu, && c_ { 1}^{(4)} = \ cos iu, \\ c_ {2}^{(1)} = 0, && c_ {2}^{(2)} = 0, && c_ {2}^{(3) } =-\ cos iu, && c_ {2}^{(4)} =-\ sin iu, \ end {matrise}} \\ {\ boldsymbol {\ downarrow}} \\ dS^{2} = (dX ' )^{2}+(dY ')^{2}+(dZ')^{2}-\ venstre (c+{\ frac {Z'c} {b}} \ høyre)^{2} dT '\ \ {\ boldsymbol {\ downarrow}} \\ c '= c+{\ frac {Z'c^{2}} {b}} \ cdot {\ frac {1} {c}} \ end {matrise}}} }$ Kottler (1914b) ${\ displaystyle \ scriptstyle {\ begin {matrix} {\ begin {matrix} c_ {1}^{(1)} = 0, && c_ {1}^{(2)} = 0, && c_ {1}^{( 3)} = {\ frac {1} {i}} \ sinh u, && c_ {1}^{(4)} = \ cosh u, \\ c_ {2}^{(1)} = 0, && c_ { 2}^{(2)} = 0, && c_ {2}^{(3)} = {\ frac {1} {i}} \ cosh u, && c_ {2}^{(4)} =-\ sinh u, \\ c_ {3}^{(1)} = 1, && c_ {3}^{(2)} = 0, && c_ {3}^{(3)} = 0, && c_ {3}^{( 4)} = 0, \\ c_ {4}^{(1)} = 0, && c_ {4}^{(2)} = 1, && c_ {4}^{(3)} = 0, && c_ {4 } ^{(4)} = 0, \ end {matrise}} \\ {\ boldsymbol {\ downarrow}} \\ X = x+\ Delta ^{(2)} c_ {2}+\ Delta ^{(3 )} c_ {3}+\ Delta ^{(4)} c_ {4} \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {align} X & = x_ {0}+{\ mathfrak {X} } '\\ Y & = y_ {0}+{\ mathfrak {Y}}' \\ Z & = \ left (b+{\ mathfrak {Z}} '\ right) \ cosh {\ mathfrak {u}} \\ cT & = \ venstre (b+{\ mathfrak {Z}} '\ høyre) \ sinh {\ mathfrak {u}} \ end {justert}} \\\ venstre (\ Delta ^{(2)} = {\ mathfrak {X }} ', \ \ Delta ^{(3)} = {\ mathfrak {Y}}', \ \ Delta ^{(4)} = {\ mathfrak {Z}} '\ right) \\ {\ boldsymbol { \ downarrow}} \\ {\ begin {align} {\ mathfrak {X}} '& = X_ {0} -x_ {0}+q_ {x} T \\ {\ mathfrak {Y}}' & = Y_ {0} -y_ {0}+q_ {y} T \\ b+{\ mathfrak {Z}} '& = {\ sqrt {\ venstre (Z_ {0}+q_ {x} T \ høyre)^{2 } -c^{2} T^{2}} } \\ c {\ mathfrak {T}} '& = b \ operatorname {artanh} {\ frac {cT} {Z_ {0}+q_ {x} T}} \ end {align}} \\\ venstre ( X = X_ {0}+q_ {x} T, \ Y = Y_ {0}+q_ {y} T, \ Z = Z_ {0}+q_ {x} T \ høyre) \\ {\ boldsymbol {\ nedoverpil}} \\ dS^{2} = (d {\ mathfrak {X}} ')^{2}+(d {\ mathfrak {Y}}')^{2}+(d {\ mathfrak {Z }} ')^{2} -c^{2} \ venstre ({\ frac {b+{\ mathfrak {Z}}'} {b^{2}}} \ høyre)^{2} (d {\ mathfrak {T}} ')^{2} \ end {matrise}}}$ Kottler (1916, 1918) ${\ displaystyle \ scriptstyle {\ begin {matrix} {\ begin {align} x & = x '\\ y & = y' \\ {\ frac {c^{2}} {\ gamma}}+z & = \ left ( {\ frac {c^{2}} {\ gamma}}+z '\ right) \ cosh {\ frac {\ gamma t'} {c}} \\ ct & = \ left ({\ frac {c^{ 2}} {\ gamma}}+z '\ right) \ sinh {\ frac {\ gamma t'} {c}} \ end {align}} \\ {\ boldsymbol {\ downarrow}} \\ ds^{ 2} = dx^{\ prime 2}+dy^{\ prime 2}+dz^{\ prime 2}-\ venstre (c+{\ frac {\ gamma} {c}} z '\ right) {}^ {2} dt^{\ prime 2} \ end {matrise}}}$

Pauli (1921) ${\ displaystyle \ scriptstyle {\ begin {matrise} {\ begin {justert} x^{1} & = \ varrho \ cos \ varphi \\ x^{4} & = \ varrho \ sin \ varphi \ end {justert} } \\ {\ boldsymbol {\ downarrow}} \\ ds ^{2} = \ left (d \ xi ^{1} \ right) ^{2}+\ left (d \ xi ^{2} \ right) ^{2}+\ venstre (d \ xi ^{3} \ høyre) ^{2}+\ venstre (\ xi ^{1} \ høyre) ^{2} \ venstre (d \ xi ^{4} \ høyre) ^{2} \\\ venstre (\ xi ^{(1)} = \ varrho, \ \ xi ^{(2)} = x ^{(2)}, \ \ xi ^{(3)} = x ^{(3)}, \ \ xi ^{(4)} = \ varphi \ right) \ end {matrise}}}$ Bollert (1922) ${\ displaystyle {\ scriptstyle {\ begin {matrix} ds^{2} = c^{2} \ venstre (1+{\ frac {\ gamma _ {0} x} {c^{2}}} \ høyre ) d \ tau^{2} -dx^{2} -dy^{2} -dz^{2} \\\ hline ds^{2} = g_ {44} dx_ {4}^{2}+g_ {11} dx_ {1}^{2}+g_ {22} \ venstre (dx_ {2}^{2}+dx_ {3}^{2} \ høyre) \\ {\ boldsymbol {\ nedoverpil}} \ \ V ''-{\ frac {g_ {11}} {2g_ {11}}} V '= 0 \\\ venstre (g_ {22} =-1, \ g_ {11} =-1, \ V' '= 0, \ V = ax+b \ right) \\ {\ boldsymbol {\ downarrow}} \\ ds^{2} = dx_ {4}^{2} (ax+b)^{2} -dx ^{2} -dy^{2} -dz^{2} \ end {matrise}}}}$ Mohorovičić (1922, 1923); Bollert (1922b) ${\ displaystyle {\ scriptstyle {\ begin {matrix} {\ text {Mohorovičić (1922):}} \\ g_ {11} = g_ {44} = V^{2}, \ VV ''-V '^{ 2} = 0, \ V \ venstre (x_ {1} \ høyre) = e^{ax_ {1}} \\ {\ boldsymbol {\ downarrow}} \\ ds^{2} = e^{2a} \ venstre (-dx_ {4}^{2}+dx_ {1}^{2} \ høyre)+dx_ {2}^{2}+dx_ {3}^{2} \\\\ {\ text {korrigert av Bollert (1922b):}} \\ ds^{2} = e^{2ax} \ left (-dx_ {4}^{2}+dx_ {1}^{2} \ right)+dx_ {2} ^{2}+dx_ {3}^{2} \\\\ {\ text {siste korreksjon av Mohorovičić (1923):}} \\ ds^{2} = e^{2ax_ {1}} \ venstre ( -dx_ {4}^{2}+dx_ {1}^{2} \ right)+dx_ {2}^{2}+dx_ {3}^{2} \ end {matrise}}}}}$ Lemaître (1924) ${\ displaystyle {\ scriptstyle {\ begin {matrise} {\ begin {justert} 1+g \ xi = & (1+gx) \ cosh gt \\ g \ tau = & (1+gx) \ sinh gt \ end {align}} \\ {\ boldsymbol {\ downarrow}} \\ ds^{2} =-dx^{2} -dy^{2} -dz^{2}+(1+gx)^{2} dt^{2} \ end {matrise}}}}$ Einstein & Rosen (1935) ${\ displaystyle \ scriptstyle {\ begin {matrise} {\ begin {align} \ xi _ {1} & = x_ {1} \ cosh \ alpha x_ {4} \\\ xi _ {2} & = x_ {2 } \\\ xi _ {3} & = x_ {3} \\\ xi _ {4} & = x_ {1} \ sinh \ alpha x_ {4} \ end {align}} \\ {\ boldsymbol {\ nedover}} \\ ds^{2} =-dx_ {1}^{2} -dx_ {2}^{2} -dx_ {3}^{2}+\ alfa {}^{2} x_ {1 }^{2} dx_ {4}^{2} \ end {matrise}}}$ Møller (1952) ${\ displaystyle \ scriptstyle {\ begin {matrix} \ alpha _ {ik} = \ left ({\ begin {matrix} U_ {4}/ic & 0 & 0 & iU_ {1}/c \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ U_ {1} /ic & 0 & 0 & U_ {4}/ic \ end {matrise}} \ høyre) \\ U_ {i} = \ venstre (c \ sinh {\ frac {g \ tau} {c}}, \ 0,0, \ ig \ cosh {\ frac {g \ tau} {c}} \ right) \\ {\ boldsymbol {\ downarrow}} \\ X_ {i} = \ mathbf {f} _ {i} (t)+x^{\ prime \ kappa} \ alpha _ {\ kappa i} (\ tau) \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {align} X & = {\ frac {c^{2}} {g}} \ venstre (\ cosh {\ frac {gt} {c}}-1 \ høyre)+x \ cosh {\ frac {gt} {c}} \\ Y & = y \\ Z & = z \\ T & = {\ frac {c} {g}} \ sinh {\ frac {gt} {c}}+x {\ frac {\ sinh {\ frac {gt} {c}}} {c}} \ end {align}} \ \ {\ boldsymbol {\ downarrow}} \\ ds^{2} = dx^{2}+dy^{2}+dz^{2} -c^{2} dt^{2} \ venstre (1+ gx/c^{2} \ right)^{2} \\\\\ end {matrise}}}$

Se også

• Bells romskipsparadoks , for et til tider kontroversielt emne som ofte studeres ved bruk av Rindler -koordinater.
• Fødte koordinater , for et annet viktig koordinatsystem tilpasset bevegelsen til visse akselererte observatører i Minkowski -romtiden .
• Kongruens (generell relativitet)
• Ehrenfest paradoks , for et til tider kontroversielt emne som ofte studeres ved hjelp av Born -koordinater.
• Rammefelt i generell relativitet
• Generelle relativitetsressurser
• Milne modell
• Raychaudhuri ligning
• Uhøflig effekt

Referanser