Curl (matematikk) - Curl (mathematics)

I vektorkalkyl er krøllen en vektoroperator som beskriver den uendelige sirkulasjonen av et vektorfelt i det tredimensjonale euklidiske rommet . Krøllen på et punkt i feltet er representert av en vektor hvis lengde og retning angir størrelsen og aksen til maksimal sirkulasjon. Krøllen til et felt er formelt definert som sirkulasjonstettheten ved hvert punkt i feltet.

Et vektorfelt hvis krøll er null kalles irrotasjonell . Krøllen er en form for differensiering for vektorfelt. Den tilsvarende formen for beregningens grunnleggende teorem er Stokes 'teorem , som knytter overflateintegralet av krøllen til et vektorfelt til linjeintegralet i vektorfeltet rundt grensekurven.

Den alternative terminologi rotasjon eller dreie og alternative notasjoner råte F eller kryssproduktet med den del (nabla) operatør ∇ x F blir noen ganger brukt for curl F . Den ISO / IEC 80000-2 standard anbefaler bruk av den råte -notasjon i uthevet skrift i motsetning til den bøyning notasjon.

I motsetning til gradienten og divergensen generaliserer ikke krøll som formulert i vektorkalkulaturen bare til andre dimensjoner; noen generaliseringer er mulige, men bare i tre dimensjoner er den geometrisk definerte krøllen til et vektorfelt igjen et vektorfelt. Denne mangelen er en direkte konsekvens av begrensningene i vektorkalkulus; når den uttrykkes via kileoperatøren for geometrisk beregning, generaliserer krøllen seg til alle dimensjoner. Den uheldige omstendigheten ligner den som deltar på det tredimensjonale kryssproduktet , og forbindelsen gjenspeiles i notasjonen ∇ × for krøllen.

Navnet "curl" ble først foreslått av James Clerk Maxwell i 1871, men konseptet ble tilsynelatende først brukt i konstruksjonen av en optisk feltteori av James MacCullagh i 1839.

Definisjon

Krøllen til et vektorfelt F , angitt med krøll F , eller ∇ × F , eller råte F , på et punkt er definert når det gjelder projeksjon på forskjellige linjer gjennom punktet. Dersom er en hvilken som helst enhetsvektor, projeksjonen av krøll på F på er definert til å være den begrensende verdi av en lukket linje integrert i et plan vinkelrett til dividert med det innelukkede området, som banen av integrasjonen er sammentrukket rundt punktet. ${\ displaystyle \ mathbf {\ hat {n}}}$${\ displaystyle \ mathbf {\ hat {n}}}$${\ displaystyle \ mathbf {\ hat {n}}}$

Krølloperatoren tilordner kontinuerlig differensierbare funksjoner f  : R ³ → R ³ til kontinuerlige funksjoner g  : R ³ → R ³ , og spesielt kartlegger den C ^k -funksjoner i R ³ til C ^{k −1} funksjoner i R ³ .

Implisitt er krøll definert på et punkt p som

${\ displaystyle (\ nabla \ times \ mathbf {F}) (p) \ cdot \ mathbf {\ hat {n}} \ {\ oversett {\ undersett {\ mathrm {def}} {}} {{} = { }}} \ lim _ {A \ til 0} {\ frac {1} {| A |}} \ oint _ {C} \ mathbf {F} \ cdot \ mathrm {d} \ mathbf {r}}$

der linjeintegralet beregnes langs grensen C til området A i spørsmålet, | A | størrelsen på området. Denne ligningen definerer projeksjonen av krøllen til F på . De uendelige overflatene som er begrenset av C har som sin normale . C er orientert via regelen til høyre . ${\ displaystyle \ mathbf {\ hat {n}}}$${\ displaystyle \ mathbf {\ hat {n}}}$

Formelen ovenfor betyr at krøllen til et vektorfelt er definert som den uendelige minimale arealtettheten til sirkulasjonen av feltet. Til denne definisjonen passer naturlig

• i Kelvin-Stokes teorem , som en global formel tilsvarer den definisjon, og
• følgende "lett å huske" definisjon av krøllen i krumme lineære ortogonale koordinater , f.eks. i kartesiske koordinater , sfæriske , sylindriske eller til og med elliptiske eller parabolske koordinater :

  ${\ displaystyle {\ begin {align} & (\ operatorname {curl} \ mathbf {F}) _ {1} = {\ frac {1} {h_ {2} h_ {3}}} \ left ({\ frac {\ partiell (h_ {3} F_ {3})} {\ delvis u_ {2}}}-{\ frac {\ delvis (h_ {2} F_ {2})} {\ delvis u_ {3}}} \ høyre), \\ [5pt] & (\ operatorname {curl} \ mathbf {F}) _ {2} = {\ frac {1} {h_ {3} h_ {1}}} \ venstre ({\ frac {\ partiell (h_ {1} F_ {1})} {\ delvis u_ {3}}}-{\ frac {\ delvis (h_ {3} F_ {3})} {\ delvis u_ {1}}} \ høyre), \\ [5pt] & (\ operatorname {curl} \ mathbf {F}) _ {3} = {\ frac {1} {h_ {1} h_ {2}}} \ venstre ({\ frac {\ partiell (h_ {2} F_ {2})} {\ delvis u_ {1}}}-{\ frac {\ delvis (h_ {1} F_ {1})} {\ delvis u_ {2}}} \ høyre). \ ende {justert}}}$

Ligningen for hver komponent (krøll F ) _k kan oppnås ved å utveksle hver forekomst av et abonnement 1, 2, 3 i syklisk permutasjon: 1 → 2, 2 → 3 og 3 → 1 (der abonnementene representerer de relevante indeksene) .

Hvis ( x ₁ , x ₂ , x ₃ ) er de kartesiske koordinatene og ( u ₁ , u ₂ , u ₃ ) er de ortogonale koordinatene, så

${\ displaystyle h_ {i} = {\ sqrt {\ venstre ({\ frac {\ partiell x_ {1}} {\ delvis u_ {i}}} \ høyre)^{2}+\ venstre ({\ frac { \ delvis x_ {2}} {\ delvis u_ {i}}} \ høyre)^{2}+\ venstre ({\ frac {\ delvis x_ {3}} {\ delvis u_ {i}}} \ høyre) ^{2}}}}$

er lengden på koordinatvektoren som tilsvarer u _i . De resterende to komponentene i krølling skyldes syklisk permutasjon av indekser : 3,1,2 → 1,2,3 → 2,3,1.

Intuitiv tolkning

Anta at vektorfeltet beskriver hastighetsfeltet til en væskestrøm (for eksempel en stor tank med væske eller gass ) og at en liten kule er plassert inne i væsken eller gassen (midten av ballen blir fikset på et bestemt punkt). Hvis ballen har en grov overflate, vil væsken som flyter forbi den få den til å rotere. Rotasjonsaksen (orientert i henhold til høyre håndregel) peker i retning av feltets krølling i midten av ballen, og rotasjonsvinkelhastigheten er halve størrelsen på krøllen på dette punktet.

Krøllen til vektoren til enhver tid er gitt ved rotasjon av et uendelig område i xy -planet (for z -aksekomponent i krøllen), zx -plan (for y -aksekomponent i krøllen) og yz -plan (for x -aksekomponent i krøllvektoren). Dette kan tydelig sees i eksemplene nedenfor.

Bruk

I praksis er definisjonen ovenfor sjelden brukt, fordi i så godt som alle tilfeller krøllen operatøren kan påføres ved hjelp av noen sett med krumme koordinater , hvor det enklere representasjoner har blitt avledet.

Notasjonen ∇ x F har sin opprinnelse i de likheter til det 3-dimensjonale vektorproduktet , og det er nyttig som et mnemonisk i kartesiske koordinater hvis ∇ er tatt som en vektor differensialoperator del . Slik notasjon som involverer operatører er vanlig i fysikk og algebra .

Utvidet med tredimensjonale kartesiske koordinater (se Del i sylindriske og sfæriske koordinater for sfæriske og sylindriske koordinatrepresentasjoner), ∇ × F er, for F sammensatt av [ F _x , F _y , F _z ] (der abonnementene angir komponentene til vektoren, ikke partielle derivater):

${\ displaystyle \ nabla \ times \ mathbf {F} = {\ begin {vmatrix} {\ boldsymbol {\ hat {\ imath}}} & {\ boldsymbol {\ hat {\ jmath}}} & {\ boldsymbol {\ hatt {k}}} \\ [5pt] {\ dfrac {\ partiell} {\ delvis x}} og {\ dfrac {\ delvis} {\ delvis y}} og {\ dfrac {\ delvis} {\ delvis z }} \\ [10pt] F_ {x} & F_ {y} & F_ {z} \ end {vmatrix}}}$

hvor i , j og k er enhetsvektorer for x -, y - og z -axes, henholdsvis. Dette utvides som følger:

${\ displaystyle \ nabla \ times \ mathbf {F} = \ left ({\ frac {\ partiell F_ {z}} {\ delvis y}}-{\ frac {\ delvis F_ {y}} {\ delvis z} } \ høyre) {\ boldsymbol {\ hat {\ imath}}}+\ venstre ({\ frac {\ delvis F_ {x}} {\ delvis z}}-{\ frac {\ delvis F_ {z}} { \ delvis x}} \ høyre) {\ boldsymbol {\ hat {\ jmath}}}+\ venstre ({\ frac {\ delvis F_ {y}} {\ delvis x}}-{\ frac {\ delvis F_ { x}} {\ delvis y}} \ høyre) {\ boldsymbol {\ hat {k}}} = {\ begynne {bmatrix} {\ frac {\ delvis F_ {z}} {\ delvis y}}-{\ frac {\ delvis F_ {y}} {\ delvis z}} \\ {\ frac {\ delvis F_ {x}} {\ delvis z}}-{\ frac {\ delvis F_ {z}} {\ delvis x }} \\ {\ frac {\ delvis F_ {y}} {\ delvis x}}-{\ frac {\ delvis F_ {x}} {\ delvis y}} \ ende {bmatrix}}}$

Selv om det er uttrykt i form av koordinater, er resultatet invariant under riktige rotasjoner av koordinataksene, men resultatet inverterer under refleksjon.

I et generelt koordinatsystem er krøllen gitt av

${\ displaystyle (\ nabla \ times \ mathbf {F}) ^{k} = {\ frac {1} {\ sqrt {g}}} \ varepsilon ^{k \ ell m} \ nabla _ {\ ell} F_ {m}}$

hvor ε betegner Levi-Civita tensoren , ∇ den kovariante derivat , er Jacobian og Einstein summerings konvensjon innebærer at gjentatte indekser blir summert over. På grunn av symmetrien til Christoffel -symbolene som deltar i kovariantderivatet, reduseres dette uttrykket til det partielle derivatet: ${\ displaystyle {\ sqrt {g}}}$

${\ displaystyle (\ nabla \ times \ mathbf {F}) = {\ frac {1} {\ sqrt {g}}} \ mathbf {R} _ {k} \ varepsilon ^{k \ ell m} \ partiell _ {l} F_ {m}}$

hvor R _k er de lokale basisvektorene. Tilsvarende, ved bruk av det utvendige derivatet , kan krøllen uttrykkes som:

${\ displaystyle \ nabla \ times \ mathbf {F} = \ left (\ star {\ big (} {\ mathrm {d}} \ mathbf {F} ^{\ flat} {\ big)} \ right) ^{ \ sharp}}$

Her ♭ og ♯ er de musikalske isomorfismene , og ★ er Hodge -stjerneoperatøren . Denne formelen viser hvordan du beregner krøllen til F i et hvilket som helst koordinatsystem, og hvordan du kan utvide krøllen til en hvilken som helst orientert tredimensjonal Riemannian manifold. Siden dette avhenger av et valg av retning, er curl en kiral operasjon. Med andre ord, hvis retningen er omvendt, blir krøllens retning også reversert.

Eksempler

Eksempel 1

Den vektorfeltet

${\ displaystyle \ mathbf {F} (x, y, z) = y {\ boldsymbol {\ hat {\ imath}}}-x {\ boldsymbol {\ hat {\ jmath}}}}}$

kan brytes ned som

${\ displaystyle \ mathbf {F} _ {x} = y, \ mathbf {F} _ {y} =-x, \ mathbf {F} _ {z} = 0.}$

Ved visuell inspeksjon kan feltet beskrives som "roterende". Hvis vektorene i feltet skulle representere en lineær kraft som virker på objekter som er tilstede på det tidspunktet, og et objekt skulle plasseres inne i feltet, ville objektet begynne å rotere med klokken rundt seg selv. Dette gjelder uansett hvor objektet er plassert.

Beregning av krøllen:

${\ displaystyle \ nabla \ times \ mathbf {F} = 0 {\ boldsymbol {\ hat {\ imath}}}+0 {\ boldsymbol {\ hat {\ jmath}}}+\ left ({\ frac {\ partial } {\ delvis x}} (-x)-{\ frac {\ delvis} {\ delvis y}} y \ høyre) {\ boldsymbol {\ hat {k}}} =-2 {\ boldsymbol {\ hat { k}}}}$

Det resulterende vektorfeltet som beskriver krøllen vil på alle punkter peke i den negative z -retningen. Resultatene av denne ligningen stemmer overens med det som kunne vært forutsagt ved hjelp av høyre håndsregel ved bruk av et høyrehendt koordinatsystem . Siden det er et jevnt vektorfelt, ville objektet beskrevet tidligere ha samme rotasjonsintensitet uavhengig av hvor det ble plassert.

Eksempel 2

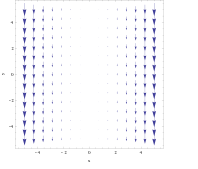
For vektorfeltet

${\ displaystyle \ mathbf {F} (x, y, z) =-x^{2} {\ boldsymbol {\ hat {\ jmath}}}}}$

krøllen er ikke like tydelig fra grafen. Imidlertid, hvis du tar objektet i forrige eksempel og plasserer det hvor som helst på linjen x = 3 , vil kraften som utøves på høyre side være litt større enn kraften som utøves til venstre, noe som får den til å rotere med klokken. Ved å bruke høyre regel kan det forutsies at den resulterende krøllen vil være rett i den negative z- retningen. Omvendt, hvis den plasseres på x = −3 , ville objektet rotere mot klokken og høyre regel ville resultere i en positiv z- retning.

Beregning av krøllen:

${\ displaystyle {\ nabla} \ times \ mathbf {F} = 0 {\ boldsymbol {\ hat {\ imath}}}+0 {\ boldsymbol {\ hat {\ jmath}}}+{\ frac {\ partial} {\ delvis x}} \ venstre (-x^{2} \ høyre) {\ boldsymbol {\ hat {k}}} =-2x {\ boldsymbol {\ hat {k}}}.}$

Krøllen peker i den negative z -retningen når x er positiv og omvendt. I dette feltet vil rotasjonsintensiteten være større ettersom objektet beveger seg bort fra planet x = 0 .

Beskrivende eksempler

• I et vektorfelt som beskriver de lineære hastighetene til hver del av en roterende skive, har krøllen den samme verdien på alle punkter.
• Av de fire Maxwells ligninger kan to - Faradays lov og Ampères lov - uttrykkes kompakt ved hjelp av krøll. Faradays lov sier at krøllen til et elektrisk felt er lik det motsatte av tidsfrekvensen for endring av magnetfeltet, mens Ampères lov relaterer magnetfeltets krølle til strømmen og endringshastigheten til det elektriske feltet.

Identiteter

Generelt krøllete koordinater (ikke bare i kartesiske koordinater) kan krøllen til et kryssprodukt av vektorfeltene v og F vise seg å være

${\ displaystyle \ nabla \ times \ left (\ mathbf {v \ times F} \ right) = {\ Big (} \ left (\ mathbf {\ nabla \ cdot F} \ right)+\ mathbf {F \ cdot \ nabla} {\ Big)} \ mathbf {v} -{\ Big (} \ left (\ mathbf {\ nabla \ cdot v} \ right)+\ mathbf {v \ cdot \ nabla} {\ Big)} \ mathbf {F} \.}$

Ved å bytte ut vektorfeltet v og ∇ -operatoren, kommer vi til tverrproduktet av et vektorfelt med krølling av et vektorfelt:

${\ displaystyle \ mathbf {v \ \ times} \ left (\ mathbf {\ nabla \ times F} \ right) = \ nabla _ {\ mathbf {F}} \ left (\ mathbf {v \ cdot F} \ right )-\ venstre (\ mathbf {v \ cdot \ nabla} \ høyre) \ mathbf {F} \,}$

der ∇ _F er Feynman -abonnementsnotasjonen, som bare vurderer variasjonen på grunn av vektorfeltet F (dvs. i dette tilfellet blir v behandlet som konstant i rommet).

Et annet eksempel er krøllen til en krøll i et vektorfelt. Det kan vises at generelt koordinater

${\ displaystyle \ nabla \ times \ left (\ mathbf {\ nabla \ times F} \ right) = \ mathbf {\ nabla} (\ mathbf {\ nabla \ cdot F})-\ nabla ^{2} \ mathbf { F} \,}$

og denne identiteten definerer vektoren Laplace-operatoren av F , symbolisert som ∇ ² F .

Curl av gradienten av en hvilken som helst skalarfelt φ er alltid null vektorfeltet

${\ displaystyle \ nabla \ times (\ nabla \ varphi) = {\ boldsymbol {0}}}$

som følger av antisymmetrien i definisjonen av krøllen, og symmetrien til andre derivater .

Hvis φ er en skalert verdifunksjon og F er et vektorfelt, så

${\ displaystyle \ nabla \ times (\ varphi \ mathbf {F}) = \ nabla \ varphi \ times \ mathbf {F} +\ varphi \ nabla \ times \ mathbf {F}}$

Generaliseringer

Vektorberegningsoperasjonene grad , curl og div blir lettest generalisert i sammenheng med differensialformer, som innebærer en rekke trinn. Kort sagt, de tilsvarer derivatene av henholdsvis 0-former, 1-former og 2-former. Den geometriske tolkningen av krøll som rotasjon tilsvarer identifisering av bivektorer (2-vektorer) i 3 dimensjoner med den spesielle ortogonale Lie-algebraen (3) av uendelige rotasjoner (i koordinater, skjevsymmetriske 3 × 3-matriser), mens representasjon av rotasjoner av vektorer tilsvarer for å identifisere 1-vektorer (ekvivalent, 2-vektorer) og (3) , alle er tredimensjonale mellomrom. ${\ displaystyle {\ mathfrak {so}}}$${\ displaystyle {\ mathfrak {so}}}$

Differensielle former

I 3 dimensjoner er en differensial 0-form ganske enkelt en funksjon f ( x , y , z ) ; en differensial 1-form er følgende uttrykk, der koeffisientene er funksjoner:

${\ displaystyle a_ {1} \, dx+a_ {2} \, dy+a_ {3} \, dz;}$

en differensial 2-form er den formelle summen, igjen med funksjonskoeffisienter:

${\ displaystyle a_ {12} \, dx \ wedge dy+a_ {13} \, dx \ wedge dz+a_ {23} \, dy \ wedge dz;}$

og en differensial 3-form er definert av et enkelt begrep med en funksjon som koeffisient:

${\ displaystyle a_ {123} \, dx \ wedge dy \ wedge dz.}$

(Her er a -koeffisientene virkelige funksjoner til tre variabler; "kileproduktene", f.eks. Dx ∧ dy , kan tolkes som en slags orienterte områdeelementer, dx ∧ dy = -dy ∧ dx , etc.)

Det utvendige derivatet av en k -form i R ³ er definert som ( k + 1) -formen ovenfra -og i R ⁿ hvis f.eks.

${\ displaystyle \ omega ^{(k)} = \ sum _ {\ scriptstyle {i_ {1} <i_ {2} <\ cdots <i_ {k}} \ atop \ forall \ scriptstyle {i _ {\ nu} \ i 1, \ ldots, n}} a_ {i_ {1}, \ ldots, i_ {k}} \, dx_ {i_ {1}} \ wedge \ cdots \ wedge dx_ {i_ {k}},}$

da fører det utvendige derivatet d til

${\ displaystyle d \ omega ^{(k)} = \ sum _ {\ scriptstyle {j = 1} \ atop \ scriptstyle {i_ {1} <\ cdots <i_ {k}}} ^{n} {\ frac {\ partiell a_ {i_ {1}, \ ldots, i_ {k}}} {\ delvis x_ {j}}} \, dx_ {j} \ kile dx_ {i_ {1}} \ kile \ cdots \ kile dx_ {i_ {k}}.}$

Det utvendige derivatet av en 1-form er derfor en 2-form, og den av en 2-form er en 3-form. På den annen side, på grunn av utbyttbarheten til blandede derivater, f.eks. På grunn av

${\ displaystyle {\ frac {\ partiell ^{2}} {\ delvis x \, \ delvis y}} = {\ frac {\ delvis ^{2}} {\ delvis y \, \ delvis x}},}$

den todelte anvendelsen av det utvendige derivatet fører til 0.

Således, ved å angi rommet til k -former med Ω ^k ( R ³ ) og det utvendige derivatet med d får en en sekvens:

${\ displaystyle 0 \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^{0} \ left (\ mathbb {R} ^{3} \ right) \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^{1} \ left (\ mathbb {R} ^{3} \ right) \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^{2} \ left ( \ mathbb {R} ^{3} \ right) \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^{3} \ left (\ mathbb {R} ^{3} \ right) \, {\ oversett {d} {\ longrightarrow}} \, 0.}$

Her er Ω ^k ( R ⁿ ) rommet til seksjoner av den ytre algebraen Λ ^k ( R ⁿ ) vektorgruppen over R ⁿ , hvis dimensjon er binomialkoeffisienten (ⁿ
_k) ; Vær oppmerksom på atΩ ^k ( R ³ ) = 0for k > 3eller k <0. Når man bare skriver dimensjoner, får man en rad avPascals trekant:

0 → 1 → 3 → 3 → 1 → 0;

de 1-dimensjonale fibrene tilsvarer skalarfelt, og de 3-dimensjonale fibrene til vektorfelt, som beskrevet nedenfor. Modulo passende identifikasjoner, de tre ikke -kommersielle forekomster av det utvendige derivatet tilsvarer grad, curl og div.

Differensialformer og differensial kan defineres på ethvert euklidisk rom, eller faktisk et mangfold, uten en forestilling om en Riemannian -metrikk. På en Riemannian manifold , eller mer generelt pseudo -Riemannian manifold , kan k -former identifiseres med k -vektorfelt ( k -former er k -covector -felt, og en pseudo -Riemannian -metrikk gir en isomorfisme mellom vektorer og covektorer), og på en orientert vektorrommet med en ikke-degenerert skjema (en isomorfi mellom vektorer og covectors), er det en isomorfi mellom k -vectors og ( n - k ) -vectors; spesielt på (tangensrommet til) en orientert pseudo-Riemannian manifold. Således på en orientert pseudo-Riemannisk manifold, kan man utveksling k formene, k -vector felt, ( n - k ) formene, og ( n - k ) -vector felt; dette er kjent som Hodge dualitet . Konkret, på R ^{3 er} dette gitt av:

• 1-former og 1-vektorfelt: 1-formen a _x dx + a _y dy + a _z dz tilsvarer vektorfeltet ( a _x , a _y , a _z ) .
• 1-former og 2-former: man erstatter dx med dobbeltmengden dy ∧ dz (dvs. utelat dx ), og på samme måte, ta vare på orientering: dy tilsvarer dz ∧ dx = -dx ∧ dz , og dz tilsvarer dx ∧ dy . Dermed tilsvarer formen a _x dx + a _y dy + a _z dz den "dobbelte formen" a _z dx ∧ dy + a _y dz ∧ dx + a _x dy ∧ dz .

Således identifiserer 0-former og 3-former med skalarfelt, og 1-former og 2-former med vektorfelt:

• grad tar et skalarfelt (0-form) til et vektorfelt (1-form);
• krøll tar et vektorfelt (1-form) til et pseudovektorfelt (2-form);
• div tar et pseudovektorfelt (2-form) til et pseudoskalært felt (3-form)

På den annen side tilsvarer det faktum at d ² = 0 identitetene

${\ displaystyle \ nabla \ times (\ nabla f) = 0}$

for ethvert skalarfelt f , og

${\ displaystyle \ nabla \ cdot (\ nabla \ times \ mathbf {v}) = 0}$

for et hvilket som helst vektorfelt v .

Grad og div generaliserer til alle orienterte pseudo-Riemanniske manifolder, med samme geometriske tolkning, fordi mellomrommene i 0-former og n- former på hvert punkt alltid er 1-dimensjonale og kan identifiseres med skalarfelt, mens mellomrommene på 1 -former og ( n -1 ) -former er alltid fibervise n -dimensjonale og kan identifiseres med vektorfelt.

Curl generaliserer ikke på denne måten til 4 eller flere dimensjoner (eller ned til 2 eller færre dimensjoner); i 4 dimensjoner er dimensjonene

0 → 1 → 4 → 6 → 4 → 1 → 0;

så krøllen til et 1-vektorfelt (fibermessig 4-dimensjonalt) er et 2-vektorfelt , som på hvert punkt tilhører det 6-dimensjonale vektorrommet, og så har man

${\ displaystyle \ omega ^{(2)} = \ sum _ {i <k = 1,2,3,4} a_ {i, k} \, dx_ {i} \ wedge dx_ {k},}$

som gir en sum av seks uavhengige termer, og som ikke kan identifiseres med et 1-vektorfelt. Man kan heller ikke meningsfullt gå fra et 1-vektorfelt til et 2-vektorfelt til et 3-vektorfelt (4 → 6 → 4), ettersom differensialet to ganger gir null ( d ² = 0 ). Dermed er det ingen curl -funksjon fra vektorfelt til vektorfelt i andre dimensjoner som oppstår på denne måten.

Imidlertid kan man definere en krøll av et vektorfelt som et 2-vektorfelt generelt, som beskrevet nedenfor.

Krøll geometrisk

2-vektorer tilsvarer utvendig effekt Λ ² V ; i nærvær av et indre produkt, i koordinater er dette de skjevsymmetriske matrisene, som er geometrisk betraktet som den spesielle ortogonale Lie-algebraen ( V ) for uendelige rotasjoner. Dette har (${\ displaystyle {\ mathfrak {so}}}$ⁿ
₂) = 1/2n ( n -1) dimensjoner, og lar en tolke differensialen til et 1-vektorfelt som dets uendelige rotasjoner. Bare i 3 dimensjoner (eller trivielt i 0 dimensjoner) betyr n =1/2n ( n - 1) , som er den mest elegante og vanlige saken. I 2 dimensjoner er krøllen til et vektorfelt ikke et vektorfelt, men en funksjon, ettersom todimensjonale rotasjoner er gitt av en vinkel (en skalar-en orientering er nødvendig for å velge om man teller rotasjoner med eller mot klokken som positive); dette er ikke div, men er ganske vinkelrett på det. I 3 dimensjoner er krøllen til et vektorfelt et vektorfelt som det er kjent (i 1 og 0 dimensjoner er krøllen til et vektorfelt 0, fordi det ikke er noen ikke-trivielle 2-vektorer), mens det i 4 dimensjoner er krøllen til et vektorfelt et vektorfelt er, geometrisk, på hvert punkt et element i den 6-dimensjonale Lie-algebraen. ${\ displaystyle {\ mathfrak {so}} (4)}$

Krøllen til et tredimensjonalt vektorfelt som bare er avhengig av 2 koordinater (si x og y ) er ganske enkelt et vertikalt vektorfelt (i z- retningen) hvis størrelse er krøllen til det todimensjonale vektorfeltet, som i eksemplene på denne siden.

Å betrakte krøll som et 2-vektorfelt (en antisymmetrisk 2-tensor) har blitt brukt til å generalisere vektorkalkulus og tilhørende fysikk til høyere dimensjoner.

Omvendt

I tilfellet der divergensen av et vektorfelt V er null, eksisterer et vektorfelt W slik at V = curl ( W ) . Dette er grunnen til at magnetfeltet , preget av null divergens, kan uttrykkes som krøllen til et magnetisk vektorpotensial .

Hvis W er et vektorfelt med curl ( W ) = V , vil det å legge til et gradientvektorfelt grad (  f  ) til W resultere i et annet vektorfelt W + grad (  f  ) slik at curl ( W + grad (  f  )) = V også. Dette kan oppsummeres ved å si at den inverse krøllen til et tredimensjonalt vektorfelt kan oppnås opp til et ukjent irrotasjonsfelt med Biot-Savart-loven .

Se også

Del av en artikkelserie om
Beregning
Grunnleggende teorem Leibniz integrert regel Grenser for funksjoner Kontinuitet Middelverdisetning Rolle -setningen
Differensial Definisjoner Derivat  ( generaliseringer ) Differensial uendelig av en funksjon Total Begreper Differensiering notasjon Andre derivat Implisitt differensiering Logaritmisk differensiering Relaterte priser Taylors teorem Regler og identiteter Sum Produkt Kjede Makt Kvotient L'Hôpital sin regel Omvendt General Leibniz Faà di Brunos formel Reynolds
Integrert Lister over integraler Integrert transformasjon Definisjoner Antiderivativ Integrert  ( feil ) Riemann integrert Lebesgue -integrasjon Konturintegrasjon Integrert omvendte funksjoner Integrasjon av Deler Plater Sylindriske skall Erstatning  ( trigonometrisk , Weierstrass , Euler ) Eulers formel Delfraksjoner Endrer rekkefølge Reduksjonsformler Differensiering under det integrerte tegnet Risch algoritme
Serie Geometrisk  ( aritmetisk-geometrisk ) Harmonisk Alternerende Makt Binomial skredder Konvergens tester Summand limit (term test) Forhold Rot Integrert Direkte sammenligning Begrens sammenligning Vekslende serie Cauchy kondens Dirichlet Abel
Vector Gradient Divergens Krøll Laplacian Retningsderivat Identiteter Satser Gradient Green's Stokes ' Divergens generaliserte Stokes
Multivariabel Formalisme Matrise Tensor Ytre Geometrisk Definisjoner Delvis derivat Flere integrerte Linje integrert Overflate integrert Volum integrert Jacobian Hessian
Spesialisert Brøkdel Malliavin Stokastisk Variasjoner
Diverse Precalculus Historie Ordliste Liste over emner Integrasjonsbi Analyse
v t e

• Helmholtz dekomponering
• Del inn sylindriske og sfæriske koordinater
• Vorticitet

Referanser

Videre lesning

• Korn, Granino Arthur og Theresa M. Korn (januar 2000). Matematisk håndbok for forskere og ingeniører: definisjoner, teoremer og formler for referanse og gjennomgang . New York: Dover Publications. s. 157–160. ISBN 0-486-41147-8.
• Schey, HM (1997). Div, Grad, Curl og alt det: En uformell tekst på vektorkalkulus . New York: Norton. ISBN 0-393-96997-5.

Eksterne linker

• "Curl" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• "Vector Calculus: Understanding Circulation and Curl - BetterExplained" . betterexplained.com . Hentet 2020-11-09 .
• "Divergens og krøll: Språket i Maxwells ligninger, Fluid Flow og mer" . 21. juni 2018 - via YouTube .