Avledninger av Lorentz -transformasjonene - Derivations of the Lorentz transformations

Del av en serie om
Romtid
Spesiell relativitet Generell relativitet
Romtidskonsepter
Generell relativitet
Klassisk tyngdekraft
Relevant matematikk
v t e

Det er mange måter å utlede Lorentz -transformasjonene ved å bruke en rekke fysiske prinsipper, alt fra Maxwells ligninger til Einsteins postulater om spesiell relativitet og matematiske verktøy, som strekker seg fra elementær algebra og hyperboliske funksjoner , til lineær algebra og gruppeteori .

Denne artikkelen gir noen av de enklere å følge i sammenheng med spesiell relativitet , for det enkleste tilfellet av et Lorentz -løft i standardkonfigurasjon, dvs. to treghetsrammer som beveger seg i forhold til hverandre med konstant (jevn) relativ hastighet mindre enn hastigheten av lys , og ved bruk av kartesiske koordinater slik at x- og x ′ -aksene er kollinære .

Lorentz transformasjon

I de grunnleggende grenene av moderne fysikk , nemlig generell relativitet og dens allment gjeldende delmengde spesialrelativitet , så vel som relativistisk kvantemekanikk og relativistisk kvantefeltteori , er Lorentz-transformasjonen transformasjonsregelen der alle fire-vektorer og tensorer som inneholder fysiske størrelser transformeres. fra en referanseramme til en annen.

De viktigste eksemplene på slike fire vektorer er de fire posisjonene og fire momentumene til en partikkel , og for felt den elektromagnetiske tensoren og stressenergietensoren . Det faktum at disse objektene transformerer i henhold til Lorentz -transformasjonen, er det som matematisk definerer dem som vektorer og tensorer; se tensor for en definisjon.

Gitt komponentene i de fire vektorene eller tensorene i en eller annen ramme, lar "transformasjonsregelen" en bestemme de endrede komponentene til de samme fire vektorene eller tensorene i en annen ramme, som kan forsterkes eller akselereres i forhold til den opprinnelige rammen. Et "løft" bør ikke være i konflikt med romlig oversettelse , det er snarere preget av den relative hastigheten mellom rammene. Selve transformasjonsregelen avhenger av den relative bevegelsen til rammene. I det enkleste tilfellet av to treghetsrammer går den relative hastigheten mellom inn i transformasjonsregelen. For roterende referanserammer eller generelle ikke-treghetsreferanserammer , trengs flere parametere, inkludert relativ hastighet (størrelse og retning), rotasjonsaksen og vinkelen som er snudd.

Historisk bakgrunn

Den vanlige behandlingen (f.eks. Albert Einsteins originale verk) er basert på variasjonen i lysets hastighet. Dette er imidlertid ikke nødvendigvis utgangspunktet: faktisk (som det avsløres, for eksempel i andre bind av The Course of Theoretical Physics av Landau og Lifshitz ), er det som virkelig står på spill lokaliteten av interaksjoner: man antar at påvirke at en partikkel, si, utøver på en annen, ikke kan overføres øyeblikkelig. Derfor eksisterer det en teoretisk maksimal hastighet for informasjonsoverføring som må være variabel, og det viser seg at denne hastigheten sammenfaller med lysets hastighet i vakuum. Newton hadde selv kalt ideen om handling på avstand filosofisk sett "absurd", og mente at tyngdekraften måtte overføres av en agent i henhold til visse lover.

Michelson og Morley i 1887 designet et eksperiment med et interferometer og et halvsølvet speil, som var nøyaktig nok til å oppdage eterstrøm. Speilsystemet reflekterte lyset tilbake til interferometeret. Hvis det var en eterdrift, ville det gi et faseskift og en endring i interferensen som ville bli oppdaget. Imidlertid ble det aldri funnet noen faseforskyvning. Det negative resultatet av Michelson - Morley -eksperimentet lot konseptet om eter (eller dets drift) undergraves. Det var følgelig forvirring om hvorfor lys åpenbart oppfører seg som en bølge, uten noe påvisbart medium som bølgeaktivitet kan spre seg gjennom.

I et papir fra 1964 viste Erik Christopher Zeeman at årsakssammenhengens bevaring av eiendom, en tilstand som er svakere i matematisk forstand enn invariansen i lysets hastighet, er nok til å sikre at koordinatforvandlingene er Lorentz -transformasjonene. Norman Goldsteins papir viser et lignende resultat ved å bruke treghet (bevaring av tidslignende linjer) i stedet for årsakssammenheng .

Fysiske prinsipper

Einstein baserte sin teori om spesiell relativitet på to grunnleggende postulater . For det første er alle fysiske lover de samme for alle treghetsrammer, uavhengig av deres relative bevegelsestilstand; og for det andre er lysets hastighet i ledig plass den samme i alle treghetsrammer, igjen, uavhengig av den relative hastigheten til hver referanseramme. Lorentz -transformasjonen er i utgangspunktet en direkte konsekvens av dette andre postulatet.

Det andre postulatet

Anta det andre postulatet om spesiell relativitet som angir lysets hastighet, uavhengig av referanserammen, og vurder en samling referansesystemer som beveger seg i forhold til hverandre med konstant hastighet, dvs. treghetssystemer , hver utstyrt med sitt eget sett med kartesisk koordinerer merking av punktene, dvs. hendelser i romtiden. For å uttrykke ujevnheten til lysets hastighet i matematisk form, fikser du to hendelser i romtiden, som skal registreres i hver referanseramme. La den første hendelsen være utslipp av et lyssignal, og den andre hendelsen være den blir absorbert.

Velg en referanseramme i samlingen. I sine koordinater vil den første hendelsen bli tildelt koordinater , og den andre . Den romlige avstanden mellom utslipp og absorpsjon er , men dette er også distansen som signalet reiser. Man kan derfor sette opp ligningen ${\ displaystyle x_ {1}, y_ {1}, z_ {1}, ct_ {1}}$${\ displaystyle x_ {2}, y_ {2}, z_ {2}, ct_ {2}}$${\ textstyle {\ sqrt {(x_ {2} -x_ {1})^{2}+(y_ {2} -y_ {1})^{2}+(z_ {2} -z_ {1}) ^{2}}}}$${\ displaystyle c (t_ {2} -t_ {1})}$

${\ displaystyle c^{2} (t_ {2} -t_ {1})^{2}-(x_ {2} -x_ {1})^{2}-(y_ {2} -y_ {1} )^{2}-(z_ {2} -z_ {1})^{2} = 0.}$

Hvert annet koordinatsystem vil registrere den samme ligningen i sine egne koordinater. Dette er den umiddelbare matematiske konsekvensen av invariansen av lysets hastighet. Mengden til venstre kalles romtiden . Intervallet er, for hendelser atskilt med lyssignaler, det samme (null) i alle referanserammer, og kalles derfor invariant .

Variasjon av intervall

For Lorentz-transformasjonen for å ha den fysiske betydning realisert av natur, er det avgjørende at intervallet er en invariant mål for eventuelle to hendelser, ikke bare for de som er adskilt av lyssignaler. For å fastslå dette, vurderer man et uendelig intervall,

${\ displaystyle ds^{2} = c^{2} dt^{2} -dx^{2} -dy^{2} -dz^{2},}$

som registrert i et system . La oss være et annet system som tildeler intervallet til de samme to uendelig adskilte hendelsene. Siden hvis , så vil intervallet også være null i ethvert annet system (andre postulat), og siden og er uendelige tall av samme rekkefølge, må de være proporsjonale med hverandre, ${\ displaystyle K}$${\ displaystyle K '}$${\ displaystyle ds '^{2}}$${\ displaystyle ds^{2} = 0}$${\ displaystyle ds^{2}}$${\ displaystyle ds '^{2}}$

${\ displaystyle ds^{2} = ads '^{2}.}$

Hva kan avhenge av? Det er kanskje ikke avhengig av posisjonene til de to hendelsene i romtiden, fordi det ville krenke den postulerte homogeniteten i romtiden . Det kan avhenge av den relative hastigheten mellom og , men bare av hastigheten, ikke av retningen, fordi sistnevnte ville krenke isotropien i rommet . ${\ displaystyle a}$${\ displaystyle V '}$${\ displaystyle K}$${\ displaystyle K '}$

Nå bringe i systemer og , ${\ displaystyle K_ {1}}$${\ displaystyle K_ {2}}$

${\ displaystyle ds^{2} = a (V_ {1}) ds_ {1}^{2}, \ quad ds^{2} = a (V_ {2}) ds_ {2}^{2}, \ quad ds_ {1}^{2} = a (V_ {12}) ds_ {2}^{2}.}$

Av disse følger det,

${\ displaystyle {\ frac {a (V_ {2})} {a (V_ {1})}} = a (V_ {12}).}$

Nå observerer man det på høyre side som er avhengig av både og ; samt på vinkelen mellom vektorene og . Imidlertid observerer man også at venstre side ikke er avhengig av denne vinkelen. Dermed er den eneste måten for ligningen å holde sant, hvis funksjonen er en konstant. Videre er denne konstanten enhet i samme ligning. Og dermed, ${\ displaystyle V_ {12}}$${\ displaystyle V_ {1}}$${\ displaystyle V_ {2}}$ ${\ displaystyle {\ textbf {V}} _ {1}}$${\ displaystyle {\ textbf {V}} _ {2}}$${\ displaystyle a (V)}$

${\ displaystyle ds^{2} = ds '^{2}}$

for alle systemer . Siden dette gjelder for alle uendelige intervaller, gjelder det for alle intervaller. ${\ displaystyle K '}$

De fleste, om ikke alle, avledningene av Lorentz -transformasjonene tar dette for gitt [Det er uklart hva dette er. Er `dette 'at rom-tidsintervallene er like? Eller er det dette som gjelder for alle uendelige intervaller også for alle intervaller? ]. I disse avledningene bruker de kun lysets hastighet (variasjon av lyslignende atskilte hendelser). Dette resultatet sikrer at Lorentz -transformasjonen er den riktige transformasjonen [Igjen er det uklart hva 'Dette' refererer til].

Rigorøs erklæring og bevis på proporsjonalitet mellom ds ² og ds ′ ²

Teorem: La være heltall, og en vektor plass i løpet av dimensjon . La det være et ubestemt indre produkt på med signaturtype . Anta er en symmetrisk Bilineær skjemaet slik at null sett den tilhørende kvadratisk form av finnes i det av (dvs. anta at for hver , hvis da ). Deretter eksisterer det en konstant slik . Videre, hvis vi antar at og som også har signaturtype , så har vi det . ${\ displaystyle n, p \ geq 1}$${\ displaystyle d: = n+p}$${\ displaystyle V}$${\ displaystyle {\ mathbb {R}}}$ ${\ displaystyle d}$${\ displaystyle h}$${\ displaystyle V}$${\ displaystyle (n, p)}$${\ displaystyle g}$${\ displaystyle V}$${\ displaystyle h}$${\ displaystyle g}$${\ displaystyle v \ in V}$${\ displaystyle h (v, v) = 0}$${\ displaystyle g (v, v) = 0}$${\ displaystyle C \ i {\ mathbb {R}}}$${\ displaystyle g = Ch}$${\ displaystyle n \ neq p}$${\ displaystyle g}$${\ displaystyle (n, p)}$${\ displaystyle C> 0}$

Merknader.

• I avsnittet ovenfor refererer begrepet "uendelig" i forhold til faktisk (punktvis) til en kvadratisk form over et fire-dimensjonalt reelt vektorrom (nemlig tangensrommet på et punkt i romtiden-manifolden). Argumentet ovenfor er kopiert nesten ordrett fra Landau og Lifshitz, hvor proporsjonaliteten til og bare er uttalt som et "åpenbart" faktum, selv om utsagnet ikke er formulert på en matematisk presis måte eller er bevist. Dette er et ikke-åpenbart matematisk faktum som må begrunnes; heldigvis er beviset relativt enkelt, og det utgjør grunnleggende algebraiske observasjoner og manipulasjoner.${\ displaystyle ds^{2}}$${\ displaystyle ds^{2}}$${\ displaystyle ds '^{2}}$

• De ovennevnte forutsetninger om innebærer følgende: er en bilineær skjema som er symmetriske og ikke-degenererte , slik at det eksisterer en ordnet basis av for hvilke${\ displaystyle h}$${\ displaystyle h: V \ ganger V \ til {\ mathbb {R}}}$ ${\ displaystyle \ {v_ {1}, \ dots, v_ {n}, v_ {n+1}, \ dots, v_ {d} \}}$${\ displaystyle V}$
  $${\ displaystyle h (v_ {a}, v_ {b}) = {\ start {cases} -1 & {\ text {if}} a = b \ in \ {1, \ dots, n \} \\ 1 & { \ tekst {if}} a = b \ i \ {n+1, \ prikker, d \} \\ 0 og {\ tekst {ellers}} \ slutt {tilfeller}}}$$

  
  En tilsvarende måte å si dette på er den som har matrisepresentasjonen i forhold til det bestilte grunnlaget .${\ displaystyle h}$${\ displaystyle {\ begin {pmatrix} -I_ {n} & 0 \\ 0 & I_ {p} \ end {pmatrix}}}$${\ displaystyle \ {v_ {1}, \ dots, v_ {d} \}}$

• Hvis vi vurderer det spesielle tilfellet der vi har å gjøre med situasjonen med Lorentzian signatur i 4-dimensjoner, som er relativitetens grunnlag påvirke sannheten i teoremet). I dette tilfellet, hvis vi antar og begge har kvadratiske former med samme nullsett (i fysikkterminologi, sier vi det og gir opphav til den samme lyskjeglen), forteller teoremet oss at det er en konstant slik at . Modulo noen forskjeller i notasjon, dette er nettopp det som ble brukt i delen ovenfor .${\ displaystyle n = 1, p = 3}$${\ displaystyle g}$${\ displaystyle h}$${\ displaystyle g}$${\ displaystyle h}$${\ displaystyle C> 0}$${\ displaystyle g = Ch}$

Bevis for teorem.

For enkelhets skyld, la oss si oss enige i dette beviset på at greske indekser liker å strekke seg over mens latinske indekser liker å strekke seg over . Vi skal også bruke Einstein -summasjonskonvensjonen gjennomgående. ${\ displaystyle \ alpha, \ beta}$${\ displaystyle \ {1, \ dots, n \}}$${\ displaystyle i, j}$${\ displaystyle \ {n+1, \ prikker, p \}}$

Fastsette et grunnlag for relativ som har matrisepresentasjonen . Også, for hver og med enhet Euklidisk norm vurdere vektoren . Så, ved bilinearitet vi har , derfor har vi også antatt det . Ved bruk av bilinearitet og symmetri av tilsvarer dette ${\ displaystyle \ {v_ {1}, \ dots, v_ {d} \}}$${\ displaystyle V}$${\ displaystyle h}$${\ displaystyle [h] = {\ begin {pmatrix} -I_ {n} & 0 \\ 0 & I_ {p} \ end {pmatrix}}}$${\ displaystyle x = (x^{1}, \ dots, x^{n}) \ i {\ mathbb {R}}^{n}}$${\ displaystyle y = (y^{n+1} \ dots, y^{n+p}) \ in {\ mathbb {R}}^{p}}$${\ displaystyle w = x^{\ alpha} v _ {\ alpha}+y^{i} v_ {i} \ i V}$${\ displaystyle h (w, w) =-\ lVert x \ rVert ^{2}+\ lVert y \ rVert ^{2} =-1+1 = 0}$${\ displaystyle g (w, w) = 0}$${\ displaystyle g}$

${\ displaystyle g _ {\ alpha \ beta} x^{\ alpha} x^{\ beta}+2g _ {\ alpha i} x^{\ alpha} y^{i}+g_ {ij} y^{i} y^{j} = 0.}$

Siden dette er sant for alle enhetsnormer, kan vi erstatte med å få ${\ displaystyle x, y}$${\ displaystyle y}$${\ displaystyle -y}$

${\ displaystyle g _ {\ alpha \ beta} x^{\ alpha} x^{\ beta} -2g _ {\ alpha i} x^{\ alpha} y^{i}+g_ {ij} y^{i} y^{j} = 0.}$

Nå trekker vi disse to ligningene og deler med 4 for å oppnå det for hele enhetsnormen, ${\ displaystyle x, y}$

${\ displaystyle g _ {\ alpha i} x^{\ alpha} y^{i} = 0.}$

Så, ved å velge og (dvs. med 1 i den angitte indeksen og 0 andre steder), ser vi at Som et resultat av dette er vår første ligning forenklet til ${\ displaystyle x = e _ {\ alpha} \ in {\ mathbb {R}}^{n}}$${\ displaystyle y = e_ {i} \ in {\ mathbb {R}}^{p}}$${\ displaystyle g _ {\ alpha i} = 0}$

${\ displaystyle g _ {\ alpha \ beta} x^{\ alpha} x^{\ beta} =-g_ {ij} y^{i} y^{j}.}$

Dette gjelder nok en gang for alle og for enhetsnormen. Som et resultat forsvinner alle de off-diagonale begrepene; mer detaljert, anta at det er forskjellige indekser. Vurder . Siden høyre side av ligningen ikke er avhengig av , ser vi det og dermed . Ved et nesten identisk argument utledes vi at hvis er forskjellige indekser da . ${\ displaystyle x \ i {\ mathbb {R}}^{n}}$${\ displaystyle y \ in {\ mathbb {R}}^{p}}$${\ displaystyle \ alpha, \ beta \ in \ {1, \ dots, n \}}$${\ textstyle x _ {\ pm} = {\ frac {1} {\ sqrt {2}}} (e _ {\ alpha} \ pm e _ {\ beta})}$${\ displaystyle x}$${\ displaystyle g _ {\ alpha \ beta} =-g _ {\ alpha \ beta}}$${\ displaystyle g _ {\ alpha \ beta} = 0}$${\ displaystyle i, j \ in \ {n+1, \ dots, n+p \}}$${\ displaystyle g_ {ij} = 0}$

Til slutt, ved å suksessivt la rekkevidde over og deretter la rekkevidde over , ser vi det ${\ displaystyle x}$${\ displaystyle e_ {1}, \ dots, e_ {n} \ in {\ mathbb {R}}^{n}}$${\ displaystyle y}$${\ displaystyle e_ {1}, \ dots, e_ {p} \ in {\ mathbb {R}}^{p}}$

${\ displaystyle -g_ {11} = \ dots = -g_ {nn} = g_ {n+1, n+1} = \ dots = g_ {n+p, n+p}}$,

eller med andre ord, har matrisepresentasjonen , som tilsvarer å si . Så proporsjonalitetskonstanten som hevdes i teoremet er . Til slutt, hvis vi antar at begge har signaturtyper og deretter (vi kan ikke ha fordi det ville bety , noe som er umulig siden å ha signaturtype betyr at det er en ikke-null bilinær form. Også, hvis det betyr at det har positiv diagonal oppføringer og negative diagonale oppføringer, dvs. det er signatur , siden vi antok , så dette er heller ikke mulig. Dette etterlater oss som det eneste alternativet). Dette fullfører beviset på teoremet. ${\ displaystyle g}$${\ displaystyle [g] =-g_ {11} \ cdot {\ begin {pmatrix} -I_ {n} & 0 \\ 0 & I_ {p} \ end {pmatrix}}}$${\ displaystyle g = -g_ {11} \ cdot h}$${\ displaystyle C = -g_ {11}}$${\ displaystyle g, h}$${\ displaystyle (n, p)}$${\ displaystyle n \ neq p}$${\ displaystyle C: =-g_ {11}> 0}$${\ displaystyle C = 0}$${\ displaystyle g = 0}$${\ displaystyle (n, p)}$${\ displaystyle C <0}$${\ displaystyle g}$${\ displaystyle n}$${\ displaystyle p}$${\ displaystyle (p, n) \ neq (n, p)}$${\ displaystyle n \ neq p}$${\ displaystyle C> 0}$

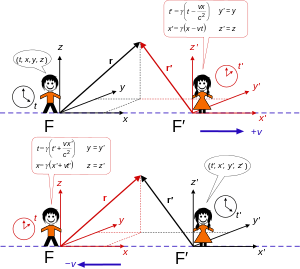
Standard konfigurasjon

Det invariante intervallet kan sees på som en ikke-positiv bestemt avstandsfunksjon i romtiden. Settet med transformasjoner som søkes må forlate denne avstanden uforanderlig. På grunn av referanserammens koordinatsystems kartesiske natur, konkluderer man med at, som i det euklidiske tilfellet, består de mulige transformasjonene av oversettelser og rotasjoner, der en litt bredere mening bør tillates for begrepet rotasjon.

Intervallet er ganske trivielt uforanderlig under oversettelse. For rotasjoner er det fire koordinater. Derfor er det seks rotasjonsplan. Tre av disse er rotasjoner i romlige plan. Intervallet er også variabelt under vanlige rotasjoner.

Det gjenstår å finne en "rotasjon" i de tre gjenværende koordinatplanene som forlater intervallet invariant. Tilsvarende for å finne en måte å tildele koordinater slik at de sammenfaller med koordinatene som tilsvarer en bevegelig ramme.

Det generelle problemet er å finne en slik transformasjon

${\ displaystyle {\ begynne {justert} & \, \, \, \, \, \, \, \, c^{2} (t_ {2} -t_ {1})^{2}-(x_ { 2} -x_ {1})^{2}-(y_ {2} -y_ {1})^{2}-(z_ {2} -z_ {1})^{2} \\ & = c^ {2} (t_ {2} '-t_ {1}')^{2}-(x_ {2} '-x_ {1}')^{2}-(y_ {2} '-y_ {1} ')^{2}-(z_ {2}'-z_ {1} ')^{2}. \ Ende {justert}}}$

For å løse det generelle problemet kan man bruke kunnskapen om invarians av intervallet for oversettelser og vanlige rotasjoner for å anta, uten tap av generalitet, at rammene F og F ′ er justert på en slik måte at deres koordinatakser alle møtes ved t = t ′ = 0 og at x og x ′ aksene er permanent justert og system F ′ har hastighet V langs den positive x -aksen . Kall dette standardkonfigurasjonen . Det reduserer det generelle problemet til å finne en transformasjon slik

${\ displaystyle c^{2} (t_ {2} -t_ {1})^{2}-(x_ {2} -x_ {1})^{2} = c^{2} (t_ {2} '-t_ {1}')^{2}-(x_ {2} '-x_ {1}')^{2}.}$

Standardkonfigurasjonen brukes i de fleste eksempler nedenfor. En lineær løsning på det enklere problemet

${\ displaystyle c^{2} t^{2} -x^{2} = c^{2} t '^{2} -x'^{2}}$

løser den mer generelle problemet siden koordinere forskjeller deretter forvandle på samme måte. Linearitet antas eller argumenteres ofte på en eller annen måte i litteraturen når dette enklere problemet vurderes. Hvis løsningen på det enklere problemet ikke er lineær, løser det ikke det opprinnelige problemet på grunn av kryssordene som vises når du utvider rutene.

Løsningene

Som nevnt er det generelle problemet løst med oversettelser i romtiden. Disse fremstår ikke som en løsning på det enklere problemet, mens boostene gjør det (og noen ganger rotasjoner avhengig av angrepsvinkel). Enda flere løsninger eksisterer hvis man bare insisterer på at intervallet ikke skal variere for lyslignende atskilte hendelser. Dette er ikke -lineære konforme ("vinkelbevarende") transformasjoner. En har

Lorentz -transformasjoner ⊂ Poincaré -transformasjoner ⊂ konforme gruppetransformasjoner .

Noen fysiske ligninger er konforme invariante, f.eks. Maxwells ligninger i kildefritt rom, men ikke alle. Relevansen av de konforme transformasjonene i romtiden er foreløpig ikke kjent, men konformgruppen i to dimensjoner er svært relevant innen konform feltteori og statistisk mekanikk . Det er dermed Poincaré -gruppen som trekkes frem av postulatene om spesiell relativitet. Det er tilstedeværelsen av Lorentz -booster (for hvilke hastighetstilsetning er forskjellig fra bare vektortilsetning som ville tillate hastigheter større enn lysets hastighet) i motsetning til vanlige boosts som skiller den fra den galileiske gruppen av galileisk relativitet . Romlige rotasjoner, romlige og tidsmessige inversjoner og oversettelser er tilstede i begge grupper og har de samme konsekvensene i begge teoriene (bevaringslover for momentum, energi og vinkelmoment). Ikke alle aksepterte teorier respekterer symmetri under inversjonene.

Bruker geometrien i romtiden

Landau & Lifshitz løsning

Problemet i standardkonfigurasjonen for et løft i x -retningen , der de primede koordinatene refererer til det bevegelige systemet, løses ved å finne en lineær løsning på det enklere problemet

${\ displaystyle c^{2} t^{2} -x^{2} = c^{2} t '^{2} -x'^{2}.}$

Den mest generelle løsningen er, som kan verifiseres ved direkte substitusjon med (H1),

For å finne rollen som Ψ i de fysiske omgivelsene, registrer progresjonen til opprinnelsen til F ′ , dvs. x ′ = 0, x = vt . Likningene blir (ved å bruke første x ′ = 0 ),

${\ displaystyle x = ct '\ sinh \ Psi, \ quad ct = ct' \ cosh \ Psi.}$

Del nå:

${\ displaystyle {\ frac {x} {ct}} = \ tanh \ Psi = {\ frac {v} {c}} \ Rightarrow \ quad \ sinh \ Psi = {\ frac {\ frac {v} {c} } {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}}, \ quad \ cosh \ Psi = {\ frac {1} {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}}}$

hvor x = vt ble brukt i det første trinnet, (H2) og (H3) i det andre, som, når det kobles til ( 1 ), gir

${\ displaystyle x = {\ frac {x '+vt'} {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}}, \ quad t = {\ frac {t '+{\ frac {v} {c^{2}}} x'} {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}},}$

eller, med de vanlige forkortelsene,

Denne beregningen gjentas med flere detaljer i seksjonen hyperbolsk rotasjon .

Hyperbolisk rotasjon

Lorentz -transformasjonene kan også utledes ved enkel anvendelse av de spesielle relativitetspostulatene og bruk av hyperboliske identiteter .

Relativitet postulerer

Start fra ligningene for den sfæriske bølgen foran en lyspuls, sentrert ved opprinnelsen:

${\ displaystyle (ct)^{2}-(x^{2}+y^{2}+z^{2}) = (ct ')^{2}-(x'^{2}+y ' ^{2}+z '^{2}) = 0}$

som har samme form i begge rammer på grunn av de spesielle relativitetspostulatene. Vurder deretter relativ bevegelse langs x -aksene til hver ramme, i standardkonfigurasjon ovenfor, slik at y = y ′, z = z ′, noe som forenkler

${\ displaystyle (ct)^{2} -x^{2} = (ct ')^{2} -x'^{2}}$

Linjæritet

Anta nå at transformasjonene har den lineære formen:

${\ displaystyle {\ begin {align} x '& = Ax+Bct \\ ct' & = Cx+Dct \ end {align}}}$

hvor A , B , C , D er å finne. Hvis de var ikke-lineære, ville de ikke ha samme form for alle observatører, siden fiktive krefter (derav akselerasjoner) ville forekomme i en ramme, selv om hastigheten var konstant i en annen, noe som er uforenlig med treghetsrammetransformasjoner.

Erstatter det forrige resultatet:

${\ displaystyle (ct)^{2} -x^{2} = [(Cx)^{2}+(Dct)^{2}+2CDcxt]-[(Ax)^{2}+(Bct)^ {2}+2ABcxt]}$

og sammenligning av koeffisienter på x ² , t ² , xt :

${\ displaystyle {\ begin {align} -1 = C^{2} -A^{2} & \ Rightarrow & A^{2} -C^{2} = 1 \\ c^{2} = (Dc) ^{2}-(Bc)^{2} & \ Rightarrow & D^{2} -B^{2} = 1 \\ 2CDc-2ABc = 0 & \ Rightarrow & AB = CD \ end {align}}}$

Hyperbolisk rotasjon

Ligningene antyder den hyperboliske identiteten ${\ displaystyle \ cosh ^{2} \ phi -\ sinh ^{2} \ phi = 1.}$

Vi presenterer hurtighet parameter φ som et hyperbolsk vinkel tillater de konsistente identifikasjoner

${\ displaystyle A = D = \ cosh \ phi \ ,, \ quad C = B =-\ sinh \ phi}$

der tegnene etter kvadratrøttene velges slik at x og t øker. De hyperboliske transformasjonene er løst for:

${\ displaystyle {\ begynne {justert} x '& = x \ cosh \ phi -ct \ sinh \ phi \\ ct' & = -x \ sinh \ phi +ct \ cosh \ phi \ end {align}}}$

Hvis skiltene ble valgt annerledes, må posisjon og tidskoordinater byttes ut med - x og/eller - t slik at x og t økning ikke reduseres.

For å finne ut hvordan ϕ forholder seg til den relative hastigheten, måles opprinnelsen til den primede rammen x ′ = 0 i den uprimmede rammen fra standardkonfigurasjonen til x = vt (eller tilsvarende og motsatt vei; opprinnelsen til den ikke -primede rammen er x = 0 og i den primede rammen er den på x ′ = - vt ):

${\ displaystyle 0 = vt \ cosh \ phi -ct \ sinh \ phi \, \ Rightarrow \, \ tanh \ phi = {\ frac {v} {c}} = \ beta}$

og manipulering av hyperboliske identiteter fører til forholdet mellom β , γ og ϕ ,

${\ displaystyle \ cosh \ phi = \ gamma, \, \ quad \ sinh \ phi = \ beta \ gamma \ ,.}$

Fra fysiske prinsipper

Problemet er vanligvis begrenset til to dimensjoner ved å bruke en hastighet langs x -aksen slik at y- og z -koordinatene ikke griper inn, som beskrevet i standardkonfigurasjonen ovenfor.

Tidsutvidelse og lengdekontraksjon

Transformasjonsligningene kan stammer fra tidsutvidelse og lengdesammentrekning , som igjen kan avledes fra første prinsipper. Med O og O ′ som representerer den romlige opprinnelsen til rammene F og F ′ , og en hendelse M , er forholdet mellom posisjonsvektorene (som her reduserer til orienterte segmenter OM , OO ′ og O′M ) gitt i begge rammene :

OM = OO ′ + OMS .

Ved å bruke koordinatene ( x , t ) i F og ( x ′, t ′) i F ′ for hendelse M, i rammen F er segmentene OM = x , OO ′ = vt og O′M = x ′ / γ (siden x ′ Er O′M målt i F ′ ):

${\ displaystyle x = vt+x '/\ gamma.}$

På samme måte, i rammen F ′ , er segmentene OM = x / γ (siden x er OM målt i F ), OO ′ = vt ′ og O′M = x ′ :

${\ displaystyle x/\ gamma = vt '+x'.}$

Ved å omorganisere den første ligningen får vi

${\ displaystyle x '= \ gamma (x-vt),}$

som er romdelen av Lorentz -transformasjonen. Det andre forholdet gir

${\ displaystyle x = \ gamma (x '+vt'),}$

som er den inverse av romdelen. Eliminering av x ′ mellom de to romdelligningene gir

${\ displaystyle t '= \ gamma (t-vx/c^{2}),}$

som er tidsdelen av transformasjonen, hvis inverse blir funnet ved en lignende eliminering av x :

${\ displaystyle t = \ gamma (t '+vx'/c^{2}).}$

Sfæriske bølgefronter av lys

Følgende ligner på Einstein. Som i den galileiske transformasjonen , er Lorentz -transformasjonen lineær siden referanse -rammers relative hastighet er konstant som en vektor; ellers ville treghetskrefter dukke opp. De kalles treghet eller galileiske referanserammer. I henhold til relativitet er ingen galilisk referanseramme privilegert. En annen betingelse er at lysets hastighet må være uavhengig av referanserammen, i praksis av lyskildens hastighet.

Tenk på to treghetsrammer med referanse O og O ′, forutsatt at O er i ro mens O ′ beveger seg med en hastighet v i forhold til O i den positive x -retningen. Opprinnelsen til O og O ′ faller opprinnelig sammen med hverandre. Et lyssignal sendes ut fra den vanlige opprinnelsen og beveger seg som en sfærisk bølgefront. Tenk på et punkt P på en sfærisk bølgefront i en avstand r og r 'fra opprinnelsen til henholdsvis O og O '. I følge det andre postulatet i den spesielle relativitetsteorien er lysets hastighet den samme i begge rammer, så for punktet P :

${\ displaystyle {\ begin {align} r & = ct \\ r '& = ct'. \ end {align}}}$

Ligningen for en kule i ramme O er gitt av

${\ displaystyle x^{2}+y^{2}+z^{2} = r^{2}.}$

For den sfæriske bølgefronten som blir

${\ displaystyle x^{2}+y^{2}+z^{2} = c^{2} t^{2}.}$

På samme måte er ligningen av en kule i rammen O ′ gitt av

${\ displaystyle x '^{2}+y'^{2}+z '^{2} = r'^{2},}$

så den sfæriske bølgefronten tilfredsstiller

${\ displaystyle x '^{2}+y'^{2}+z '^{2} = c^{2} t'^{2}.}$

Opprinnelsen O ′ beveger seg langs x -aksen. Derfor,

${\ displaystyle {\ begin {align} y '& = y \\ z' & = z. \ end {align}}}$

x ′ må variere lineært med x og t . Derfor har transformasjonen formen

${\ displaystyle x '= \ gamma x+\ sigma t.}$

For opprinnelsen til O ′ x ' og x er gitt av

${\ displaystyle {\ begin {align} x '& = 0 \\ x & = vt, \ end {align}}}$

så, for alle t ,

${\ displaystyle 0 = \ gamma vt+\ sigma t}$

og dermed

${\ displaystyle \ sigma =-\ gamma v.}$

Dette forenkler transformasjonen til

${\ displaystyle x '= \ gamma \ venstre (x-vt \ høyre)}$

hvor γ skal bestemmes. På dette punktet er γ ikke nødvendigvis en konstant, men er nødvendig for å redusere til 1 for v ≪ c .

Den omvendte transformasjonen er den samme bortsett fra at tegnet på v er reversert:

${\ displaystyle x = \ gamma \ left (x '+vt' \ right).}$

De to ligningene ovenfor gir forholdet mellom t og t ′ som:

${\ displaystyle x = \ gamma \ left [\ gamma \ left (x-vt \ right)+vt '\ right]}$

eller

${\ displaystyle t '= \ gamma t+{\ frac {\ left (1-{\ gamma ^{2}} \ right) x} {\ gamma v}}.}$

Erstatte x ′, y ′, z ′ og t ′ i den sfæriske bølgefrontligningen i O ′ rammen,

${\ displaystyle x '^{2}+y'^{2}+z '^{2} = c^{2} t'^{2},}$

med sine uttrykk i form av x , y , z og t produserer:

${\ displaystyle {\ gamma^{2}} \ venstre (x-vt \ høyre)^{2}+y^{2}+z^{2} = c^{2} \ venstre [\ gamma t+{\ frac {\ venstre (1-{\ gamma ^{2}} \ høyre) x} {\ gamma v}} \ høyre] ^{2}}$

og derfor,

${\ displaystyle \ gamma^{2} x^{2}+\ gamma^{2} v^{2} t^{2} -2 \ gamma^{2} vtx+y^{2}+z^{ 2} = c^{2} {\ gamma^{2}} t^{2}+{\ frac {\ venstre (1-{\ gamma^{2}} \ høyre)^{2} c^{2 } x^{2}} {{\ gamma^{2}} v^{2}}}+2 {\ frac {\ venstre (1-{\ gamma^{2}} \ høyre) txc^{2} } {v}}}$

som innebærer,

${\ displaystyle \ left [{\ gamma ^{2}}-{\ frac {\ left (1-{\ gamma ^{2}} \ right) ^{2} c ^{2}} {{\ gamma ^ {2}} v^{2}}} \ høyre] x^{2} -2 {\ gamma^{2}} vtx+y^{2}+z^{2} = \ venstre (c^{2 } {\ gamma ^{2}}-v ^{2} {\ gamma ^{2}} \ høyre) t ^{2} +2 {\ frac {\ venstre [1-{\ gamma ^{2}} \ høyre] txc^{2}} {v}}}$

eller

${\ displaystyle \ left [{\ gamma ^{2}}-{\ frac {\ left (1-{\ gamma ^{2}} \ right) ^{2} c ^{2}} {{\ gamma ^ {2}} v ^{2}}} \ høyre] x ^{2}-\ venstre [2 {\ gamma ^{2}} v+2 {\ frac {\ venstre (1-{\ gamma ^{2 }} \ høyre) c^{2}} {v}} \ høyre] tx+y^{2}+z^{2} = \ venstre [c^{2} {\ gamma^{2}}-v ^{2} {\ gamma ^{2}} \ høyre] t ^{2}}$

Ved å sammenligne koeffisienten t ² i ligningen ovenfor med koeffisienten t ² i den sfæriske bølgefrontligningen for ramme O gir:

${\ displaystyle c^{2} {\ gamma^{2}}-v^{2} {\ gamma^{2}} = c^{2}}$

Tilsvarende uttrykk for γ kan oppnås ved å matche x ² -koeffisientene eller sette tx -koeffisienten til null. Omorganisering:

${\ displaystyle {\ gamma^{2}} = {\ frac {1} {1-{\ frac {v^{2}} {c^{2}}}}}}}$

eller ved å velge den positive roten for å sikre at x- og x -aksene og tidsaksene peker i samme retning,

${\ displaystyle {\ gamma} = {\ frac {1} {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}}}}}$

som kalles Lorentz -faktoren . Dette produserer Lorentz -transformasjonen fra uttrykket ovenfor. Det er gitt av

${\ displaystyle {\ begin {align} x '& = \ gamma \ left (x-vt \ right) \\ t' & = \ gamma \ left (t-{\ frac {vx} {c^{2}} } \ høyre) \\ y '& = y \\ z' & = z \ end {align}}}$

Lorentz -transformasjonen er ikke den eneste transformasjonen som etterlater invariant formen til sfæriske bølger, ettersom det er et bredere sett med sfæriske bølgetransformasjoner i kontekst av konform geometri , og etterlater invariant uttrykket . Imidlertid kan ikke konforme transformasjoner i skalaendring brukes til å symmetrisk beskrive alle naturlover inkludert mekanikk , mens Lorentz -transformasjonene (den eneste som antyder ) representerer en symmetri av alle naturlover og reduseres til galileiske transformasjoner kl . ${\ displaystyle \ lambda \ left (\ delta x^{2}+\ delta y^{2}+\ delta z^{2} -c^{2} \ delta t^{2} \ right)}$${\ displaystyle \ lambda = 1}$${\ displaystyle v \ ll c}$

Galileisk og Einsteins relativitet

Galileiske referanserammer

I klassisk kinematikk er den totale forskyvningen x i R -rammen summen av den relative forskyvningen x 'i rammen R' og av avstanden mellom de to opprinnelsene x - x '. Hvis v er den relative hastigheten til R ′ i forhold til R, er transformasjonen: x  =  x ′ +  vt , eller x ′ =  x  -  vt . Dette forholdet er lineært for en konstant v , det vil si når R og R ′ er galileiske referanserammer.

I Einsteins relativitet er hovedforskjellen fra den galileiske relativiteten at rom- og tidskoordinater er sammenflettet og i forskjellige treghetsrammer t  ≠  t ′.

Siden rommet antas å være homogent, må transformasjonen være lineær. Det mest generelle lineære forholdet oppnås med fire konstante koeffisienter, A , B , γ og b :

${\ displaystyle x '= \ gamma x+bt \,}$

${\ displaystyle t '= Ax+Bt. \,}$

Den lineære transformasjonen blir den galileiske transformasjonen når γ = B = 1, b = - v og A = 0.

Et objekt i ro i R ′ rammen ved posisjon x ′ = 0 beveger seg med konstant hastighet v i R rammen. Derfor må transformasjonen gi x ′ = 0 hvis x = vt . Derfor er b = - γv og den første ligningen skrevet som

${\ displaystyle x '= \ gamma (x-vt) \ ,.}$

Bruker relativitetens prinsipp

I henhold til relativitetsprinsippet er det ingen privilegert galilisk referanseramme: derfor bør den inverse transformasjonen for posisjonen fra rammen R ′ til rammen R ha samme form som originalen, men med hastigheten i motsatt retning, iow erstatter v med -v :

${\ displaystyle x = \ gamma \ left (x '-(-v) t' \ right),}$

og dermed

${\ displaystyle x = \ gamma \ left (x '+vt' \ right).}$

Bestemmelse av konstantene i den første ligningen

Siden lysets hastighet er den samme i alle referanserammer, for et lyssignal, må transformasjonen garantere at t  =  x / c når t ′ =  x ′ / c .

Å erstatte t og t ′ i de foregående ligningene gir:

${\ displaystyle x '= \ gamma \ venstre (1-v/c \ høyre) x,}$

${\ displaystyle x = \ gamma \ venstre (1+v/c \ høyre) x '.}$

Å multiplisere disse to ligningene gir,

${\ displaystyle xx '= \ gamma^{2} \ left (1-v^{2}/c^{2} \ right) xx'.}$

Når som helst etter t = t ′ = 0, er xx ′ ikke null, så å dele begge sider av ligningen med xx ′ resulterer i

${\ displaystyle \ gamma = {\ frac {1} {\ sqrt {1-{\ frac {v^{2}} {c^{2}}}}}}}}$

som kalles "Lorentz -faktoren".

Når transformasjonsligningene kreves for å tilfredsstille lyssignalligningene i formen x  =  ct og x ′ =  ct ′, ved å erstatte x- og x'-verdiene, produserer den samme teknikken det samme uttrykket for Lorentz-faktoren.

Bestemmelse av konstantene i den andre ligningen

Transformasjonsligningen for tid kan lett oppnås ved å vurdere det spesielle tilfellet av et lyssignal, som igjen tilfredsstiller x  =  ct og x ′ =  ct ′, ved å erstatte term for term i den tidligere oppnådde ligningen for den romlige koordinaten

${\ displaystyle x '= \ gamma (x-vt), \,}$

å gi

${\ displaystyle ct '= \ gamma \ left (ct-{\ frac {v} {c}} x \ right),}$

så det

${\ displaystyle t '= \ gamma \ left (t-{\ frac {v} {c^{2}}} x \ right),}$

som, når identifisert med

${\ displaystyle t '= Ax+Bt, \,}$

bestemmer transformasjonskoeffisientene A og B som

${\ displaystyle A =-\ gamma v/c^{2}, \,}$

${\ displaystyle B = \ gamma. \,}$

Så A og B er de unike konstante koeffisientene som er nødvendige for å bevare lysets hastighet i det primede koordinatsystemet.

Einsteins populære avledning

I sin populære bok Einstein avledet Lorentz-transformasjonen ved å hevde at det må være to ikke-null koblingskonstant X og μ slik at

${\ displaystyle {\ begin {cases} x'-ct '= \ lambda \ left (x-ct \ right) \\ x'+ct '= \ mu \ left (x+ct \ right) \, \ end { saker}}}$

som tilsvarer lys som beveger seg langs henholdsvis den positive og negative x-aksen. For lys x = ct hvis og bare hvis x ′ = ct ′ . Legge til og trekke fra de to ligningene og definere

${\ displaystyle {\ begin {cases} \ gamma = \ left (\ lambda +\ mu \ right)/2 \\ b = \ left (\ lambda -\ mu \ right)/2, \, \ end {cases} }}$

gir

${\ displaystyle {\ begin {cases} x '= \ gamma x-bct \\ ct' = \ gamma ct-bx. \, \ end {cases}}}$

Ved å erstatte x ′ = 0 som tilsvarer x = vt og merke at den relative hastigheten er v = bc / γ , gir dette

${\ displaystyle {\ begin {cases} x '= \ gamma \ left (x-vt \ right) \\ t' = \ gamma \ left (t-{\ frac {v} {c^{2}}} x \ right) \, \ end {cases}}}$

Konstanten γ kan evalueres ved å kreve c ² t ² - x ² = c ² t ′ ² - x ′ ² i henhold til standardkonfigurasjon .

Bruke gruppeteori

Fra gruppepostulater

Følgende er en klassisk avledning (se f.eks. [1] og referanser der) basert på gruppepostulater og isotropi av rommet.

Koordinere transformasjoner som en gruppe

Koordinattransformasjonene mellom treghetsrammer danner en gruppe (kalt den riktige Lorentz -gruppen ), der gruppeoperasjonen er sammensetningen av transformasjoner (utfører den ene transformasjonen etter den andre). Faktisk er de fire gruppeaksionene tilfredse:

1. Nedleggelse : sammensetningen av to transformasjoner er en transformasjon: vurdere en sammensetning av transformasjoner fra treghetsrammen K til treghetsramme K ′, (betegnet K → K ′), og deretter fra K ′ til treghetsramme K ′ ′, [ K ′ → K ′ ′], eksisterer det en transformasjon, [ K → K ′] [ K ′ → K ′ ′], direkte fra en treghetsramme K til treghetsramme K ′ ′.
2. Associativitet : transformasjonene ([ K → K ′] [ K ′ → K ′ ′]) [ K ′ → K ′ ′ ′] og [ K → K ′] ([ K ′ → K ′ ′] [ K ′ ′ → K ′ ′ ′]) er identiske.
3. Identitet element : det er en identitet element, en transformasjon K → K .
4. Invers element : for enhver transformasjon K → K 'det foreligger en invers transformasjon K ' → K .

Transformasjonsmatriser i samsvar med gruppeaksiomer

Tenk på to treghetsrammer, K og K ′, sistnevnte beveger seg med hastigheten v i forhold til førstnevnte. Ved rotasjoner og skift kan vi velge x- og x ′ -aksene langs den relative hastighetsvektoren og også at hendelsene ( t , x ) = (0,0) og ( t ′, x ′) = (0,0) sammenfaller. Siden hastighetsøkningen er langs x (og x ′ ) aksene skjer det ingenting med de vinkelrette koordinatene, og vi kan bare utelate dem for å være korte. Siden transformasjonen vi ser etter forbinder to treghetsrammer, må den transformere en lineær bevegelse i ( t , x ) til en lineær bevegelse i ( t ′, x ′) koordinater. Derfor må det være en lineær transformasjon. Den generelle formen for en lineær transformasjon er

${\ displaystyle {\ begin {bmatrix} t '\\ x' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & \ delta \\\ beta & \ alpha \ end {bmatrix}} {\ begin { bmatrix} t \\ x \ end {bmatrix}},}$

hvor α , β , γ og δ er noen ennå ukjente funksjoner for den relative hastigheten v .

La oss nå vurdere bevegelsen til opprinnelsen til rammen K ′. I K ′ rammen har den koordinater ( t ′, x ′ = 0) , mens den i K -rammen har koordinater ( t , x = vt ) . Disse to punktene er forbundet med transformasjonen

${\ displaystyle {\ begin {bmatrix} t '\\ 0 \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & \ delta \\\ beta & \ alpha \ end {bmatrix}} {\ begin {bmatrix } t \\ vt \ end {bmatrix}},}$

som vi får fra

${\ displaystyle \ beta = -v \ alpha \,}$.

Analogt sett, med tanke på bevegelsen av opprinnelsen til rammen K , får vi

${\ displaystyle {\ begin {bmatrix} t '\\-vt' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & \ delta \\\ beta & \ alpha \ end {bmatrix}} {\ begin {bmatrix} t \\ 0 \ end {bmatrix}},}$

som vi får fra

${\ displaystyle \ beta = -v \ gamma \,}$.

Ved å kombinere disse to gir α = γ og transformasjonsmatrisen har forenklet,

${\ displaystyle {\ begin {bmatrix} t '\\ x' \ end {bmatrix}} = {\ begin {bmatrix} \ gamma & \ delta \\-v \ gamma & \ gamma \ end {bmatrix}} {\ begynn {bmatrix} t \\ x \ end {bmatrix}}.}$

Tenk nå på det omvendte elementet i gruppepostulatet . Det er to måter vi kan gå fra K ′ koordinatsystemet til K koordinatsystemet. Den første er å bruke det inverse av transformasjonsmatrisen på K ′ -koordinatene:

${\ displaystyle {\ begin {bmatrix} t \\ x \ end {bmatrix}} = {\ frac {1} {\ gamma ^{2}+v \ delta \ gamma}} {\ begin {bmatrix} \ gamma & -\ delta \\ v \ gamma & \ gamma \ end {bmatrix}} {\ begin {bmatrix} t '\\ x' \ end {bmatrix}}.}$

Det andre er, med tanke på at K ′ -koordinatsystemet beveger seg med en hastighet v i forhold til K -koordinatsystemet, må K -koordinatsystemet bevege seg med en hastighet - v i forhold til K ′ -koordinatsystemet. Å erstatte v med - v i transformasjonsmatrisen gir:

${\ displaystyle {\ begin {bmatrix} t \\ x \ end {bmatrix}} = {\ begin {bmatrix} \ gamma (-v) & \ delta (-v) \\ v \ gamma (-v) & \ gamma (-v) \ end {bmatrix}} {\ begin {bmatrix} t '\\ x' \ end {bmatrix}},}$

Nå kan funksjonen γ ikke avhenge av retningen til v fordi det tilsynelatende er faktoren som definerer den relativistiske sammentrekningen og tidsutvidelsen. Disse to (i en isotrop verden av oss) kan ikke stole på retningen til v . Dermed får γ ( - v ) = γ ( v ) og sammenligning av de to matrisene

${\ displaystyle \ gamma ^{2}+v \ delta \ gamma = 1.}$

I henhold til nedleggelsesgruppepostulatet er en sammensetning av to koordinattransformasjoner også en koordinattransformasjon, og derfor bør produktet av to av våre matriser også være en matrise av samme form. Transformering K til K ′ og fra K ′ til K ′ ′ gir følgende transformasjonsmatrise for å gå fra K til K ′ ′:

${\ displaystyle {\ begin {align} {\ begin {bmatrix} t '' \\ x '' \ end {bmatrix}} & = {\ begin {bmatrix} \ gamma (v ') & \ delta (v') \\-v '\ gamma (v') & \ gamma (v ') \ end {bmatrix}} {\ begin {bmatrix} \ gamma (v) & \ delta (v) \\-v \ gamma (v) & \ gamma (v) \ end {bmatrix}} {\ begin {bmatrix} t \\ x \ end {bmatrix}} \\ & = {\ begin {bmatrix} \ gamma (v ') \ gamma (v)- v \ delta (v ') \ gamma (v) & \ gamma (v') \ delta (v)+\ delta (v ') \ gamma (v) \\-(v'+v) \ gamma (v ' ) \ gamma (v) &-v '\ gamma (v') \ delta (v)+\ gamma (v ') \ gamma (v) \ end {bmatrix}} {\ begin {bmatrix} t \\ x \ ende {bmatrix}}. \ end {align}}}$

I den opprinnelige transformasjonsmatrisen er de viktigste diagonale elementene begge lik γ , derfor må den kombinerte transformasjonsmatrisen ovenfor ha samme form som den opprinnelige transformasjonsmatrisen, de viktigste diagonale elementene må også være like. Likestilling av disse elementene og omorganisering gir:

${\ displaystyle \ gamma (v ') \ gamma (v) -v \ delta (v') \ gamma (v) =-v '\ gamma (v') \ delta (v)+\ gamma (v ') \ gamma (v) \,}$

${\ displaystyle v \ delta (v ') \ gamma (v) = v' \ gamma (v ') \ delta (v) \,}$

${\ displaystyle {\ frac {\ delta (v)} {v \ gamma (v)}} = {\ frac {\ delta (v ')} {v' \ gamma (v ')}}. \,}$

Nevneren vil være forskjellig fra null for ikke-null v , fordi γ ( v ) er alltid forskjellig fra null;

${\ displaystyle \ gamma ^{2}+v \ delta \ gamma = 1}$.

Hvis v = 0 har vi identitetsmatrisen som sammenfaller med å sette v = 0 i matrisen vi får på slutten av denne avledningen for de andre verdiene av v , noe som gjør den endelige matrisen gyldig for alle ikke -negative v .

For ikke -null v må denne kombinasjonen av funksjoner være en universell konstant, en og den samme for alle treghetsrammer. Definere denne konstant som δ ( v ) / v γ ( v ) = κ , hvor κ har den dimensjon av 1 / v ² . Løsning

${\ displaystyle 1 = \ gamma ^{2}+v \ delta \ gamma = \ gamma ^{2} (1+ \ kappa v ^{2}) \,}$

får vi endelig

${\ displaystyle \ gamma = 1/{\ sqrt {1+ \ kappa v^{2}}}}$

og dermed er transformasjonsmatrisen, i samsvar med gruppeaksionene, gitt av

${\ displaystyle {\ begin {bmatrix} t '\\ x' \ end {bmatrix}} = {\ frac {1} {\ sqrt {1+ \ kappa v^{2}}}} {\ begin {bmatrix} 1 & \ kappa v \\-v & 1 \ end {bmatrix}} {\ begin {bmatrix} t \\ x \ end {bmatrix}}.}$

Hvis κ > 0 , så ville det være transformasjoner (med κv ² ≫ 1 ) som forvandler tid til en romlig koordinat og omvendt. Vi utelukker dette på fysisk grunn, fordi tiden bare kan løpe i positiv retning. Således er to typer transformasjonsmatriser i samsvar med gruppepostulater:

Galileiske transformasjoner

Hvis κ = 0 får vi den galileiske-newtoniske kinematikken med den galileiske transformasjonen,

${\ displaystyle {\ begin {bmatrix} t '\\ x' \ end {bmatrix}} = {\ begin {bmatrix} 1 & 0 \\-v & 1 \ end {bmatrix}} {\ begin {bmatrix} t \\ x \ ende {bmatrix}} \ ;,}$

hvor tiden er absolutt, t ′ = t , og den relative hastigheten v av to treghetsrammer er ikke begrenset.

Lorentz -transformasjoner

Hvis κ <0 , så setter vi den som blir den uforanderlige hastigheten , lysets hastighet i vakuum. Dette gir κ = −1/ c ² og dermed får vi spesiell relativitet med Lorentz -transformasjon ${\ displaystyle c = 1/{\ sqrt {-\ kappa}}}$

${\ displaystyle {\ begin {bmatrix} t '\\ x' \ end {bmatrix}} = {\ frac {1} {\ sqrt {1- {v^{2} \ over c^{2}}}} } {\ begin {bmatrix} 1 & {-v \ over c^{2}} \\-v & 1 \ end {bmatrix}} {\ begin {bmatrix} t \\ x \ end {bmatrix}} \ ;,}$

der lysets hastighet er en endelig universell konstant som bestemmer høyest mulig relativ hastighet mellom treghetsrammer.

Hvis v ≪ c er den galileiske transformasjonen en god tilnærming til Lorentz -transformasjonen.

Bare eksperiment kan svare på spørsmålet hvilken av de to mulighetene, κ = 0 eller κ <0 , som er realisert i vår verden. Eksperimentene som måler lysets hastighet, først utført av en dansk fysiker Ole Rømer , viser at det er begrenset, og Michelson – Morley -eksperimentet viste at det er en absolutt hastighet, og dermed at κ <0 .

Boost fra generatorer

Ved å bruke hurtighet ϕ til å parametrisere Lorentz -transformasjonen, er boostet i x -retningen

${\ displaystyle {\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ cosh \ phi &-\ sinh \ phi & 0 & 0 \\- \ sinh \ phi & \ cosh \ phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}}, }$

på samme måte for et løft i y -retningen

${\ displaystyle {\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ cosh \ phi & 0 &-\ sinh \ phi & 0 \\ 0 & 1 & 0 & 0 \\-\ sinh \ phi & 0 & \ cosh \ phi & 0 \\ 0 & 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}}, }$

og z -retningen

${\ displaystyle {\ begin {bmatrix} ct '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ cosh \ phi & 0 & 0 &-\ sinh \ phi \\ 0 & 1 & 0 & 0 \ \ 0 & 0 & 1 & 0 \\-\ sinh \ phi & 0 & 0 & \ cosh \ phi \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}} \ ,. }$

hvor e _x , e _y , e _z er de kartesiske basisvektorene, et sett med gjensidig vinkelrette enhetsvektorer langs deres angitte retninger. Hvis en ramme økes med hastigheten v i forhold til en annen, er det praktisk å introdusere en enhetsvektor n = v / v = β / β i relativ bevegelsesretning. Det generelle løftet er

${\ displaystyle {\ begin {bmatrix} c \, t '\\ x' \\ y '\\ z' \ end {bmatrix}} = {\ begin {bmatrix} \ cosh \ phi & -n_ {x} \ sinh \ phi & -n_ {y} \ sinh \ phi & -n_ {z} \ sinh \ phi \\-n_ {x} \ sinh \ phi & 1+(\ cosh \ phi -1) n_ {x}^{2 } & (\ cosh \ phi -1) n_ {x} n_ {y} & (\ cosh \ phi -1) n_ {x} n_ {z} \\ -n_ {y} \ sinh \ phi & (\ cosh \ phi -1) n_ {y} n_ {x} & 1+(\ cosh \ phi -1) n_ {y}^{2} & (\ cosh \ phi -1) n_ {y} n_ {z} \\ - n_ {z} \ sinh \ phi & (\ cosh \ phi -1) n_ {z} n_ {x} & (\ cosh \ phi -1) n_ {z} n_ {y} & 1+(\ cosh \ phi -1 ) n_ {z}^{2} \\\ end {bmatrix}} {\ begin {bmatrix} c \, t \\ x \\ y \\ z \ end {bmatrix}} \ ,.}$

Legg merke til at matrisen avhenger av retningen til den relative bevegelsen så vel som hurtigheten, i alle tre tallene (to for retning, en for hurtighet).

Vi kan kaste hver av boostmatrisene i en annen form som følger. Vurder først boostet i x -retningen. Den Taylor ekspansjon av boost matrisen om φ = 0 er

${\ displaystyle B (\ mathbf {e} _ {x}, \ phi) = \ sum _ {n = 0} ^{\ infty} {\ frac {\ phi ^{n}} {n!}} \ venstre . {\ frac {\ partiell ^{n} B (\ mathbf {e} _ {x}, \ phi)} {\ delvis \ phi ^{n}}} \ høyre | _ {\ phi = 0}}$

der derivatene av matrisen med hensyn til ϕ er gitt ved å differensiere hver oppføring i matrisen separat, og notasjonen | _{ϕ = 0} indikerer at ϕ er satt til null etter at derivatene er evaluert. Å ekspandere til første ordre gir den uendelige transformasjonen

${\ displaystyle B (\ mathbf {e} _ {x}, \ phi) = I+\ phi \ left. {\ frac {\ partiell B} {\ partiell \ phi}} \ høyre | _ {\ phi = 0} = {\ start {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 \ 1 \ end {bmatrix}}-\ phi {\ start {bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0$

som er gyldig hvis ϕ er liten (derav ϕ ² og høyere krefter er ubetydelig), og kan tolkes som ingen boost (det første uttrykket I er 4 × 4 identitetsmatrisen), etterfulgt av et lite løft. Matrisen

${\ displaystyle K_ {x} = {\ begin {bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \ end {bmatrix}}}$

er generatoren for boostet i x -retningen, så det uendelige boostet er

${\ displaystyle B (\ mathbf {e} _ {x}, \ phi) = I- \ phi K_ {x}}$

Nå er ϕ liten, så dividering med et positivt heltall N gir et enda mindre trinn av hastighet ϕ / N , og N av disse uendelige økte vil gi det opprinnelige uendelige øket med hurtighet ϕ ,

${\ displaystyle B (\ mathbf {e} _ {x}, \ phi) = \ left (I-{\ frac {\ phi K_ {x}} {N}} \ right)^{N}}$

I grensen til et uendelig antall uendelig små trinn, får vi den endelige boost -transformasjonen

${\ displaystyle B (\ mathbf {e} _ {x}, \ phi) = \ lim _ {N \ rightarrow \ infty} \ left (I-{\ frac {\ phi K_ {x}} {N}} \ høyre)^{N} = e^{-\ phi K_ {x}}}$

som er grense definisjonen av eksponentiell på grunn av Leonhard Euler , og er nå sant for enhver ϕ .

Gjentagelse av prosessen for boostene i y- og z -retningene får de andre generatorene

${\ displaystyle K_ {y} = {\ begin {bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \ end {bmatrix}} \ ,, \ quad K_ {z} = {\ begin {bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \ end {bmatrix}}}$

og boostene er

${\ displaystyle B (\ mathbf {e} _ {y}, \ phi) = e^{-\ phi K_ {y}} \ ,, \ quad B (\ mathbf {e} _ {z}, \ phi) = e^{-\ phi K_ {z}} \ ,.}$

For alle retninger er den uendelige transformasjonen (liten ϕ og ekspansjon til første orden)

${\ displaystyle B (\ mathbf {n}, \ phi) = I+\ phi \ venstre. {\ frac {\ partiell B} {\ delvis \ phi}} \ høyre | _ {\ phi = 0} = {\ start {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ ende {bmatrix}}-\ phi {\ start {bmatrix} 0 & n_ {x} & n_ {y} & n_ {z} \\ n_ {x} & 0 & 0 \\ n_ {y} & 0 & 0 & 0 \\ n_ {z} & 0 & 0 & 0 \ end {bmatrix}}}$

hvor

${\ displaystyle {\ begin {bmatrix} 0 & n_ {x} & n_ {y} & n_ {z} \\ n_ {x} & 0 & 0 & 0 \\ n_ {y} & 0 & 0 & 0 \\ n_ {z} & 0 & 0 & 0 \ end {bmatrix}} = n_ {x} K_ {x}+n_ {y} K_ {y}+n_ {z} K_ {z} = \ mathbf {n} \ cdot \ mathbf {K}}$

er generatoren for boost i retning n . Det er full boost -generatoren, en vektor av matriser K = ( K _x , K _y , K _z ) , projisert i retningen til boost n . Det uendelige boostet er

${\ displaystyle B (\ mathbf {n}, \ phi) = I- \ phi (\ mathbf {n} \ cdot \ mathbf {K})}$

Så i grensen til et uendelig antall uendelig små trinn, får vi den endelige boost -transformasjonen

${\ displaystyle B (\ mathbf {n}, \ phi) = \ lim _ {N \ rightarrow \ infty} \ left (I-{\ frac {\ phi (\ mathbf {n} \ cdot \ mathbf {K}) } {N}} \ right)^{N} = e^{-\ phi (\ mathbf {n} \ cdot \ mathbf {K})}}$

som nå er sant for enhver ϕ . Utvider matrisens eksponensial av - ϕ ( n ⋅ K ) i sin kraftserie

${\ displaystyle e^{-\ phi \ mathbf {n} \ cdot \ mathbf {K}} = \ sum _ {n = 0}^{\ infty} {\ frac {1} {n!}} (-\ phi \ mathbf {n} \ cdot \ mathbf {K})^{n}}$

vi trenger nå generatorens krefter. Torget er

${\ displaystyle (\ mathbf {n} \ cdot \ mathbf {K})^{2} = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & n_ {x}^{2} & n_ {x} n_ {y} & n_ {x } n_ {z} \\ 0 og n_ {y} n_ {x} & n_ {y}^{2} & n_ {y} n_ {z} \\ 0 & n_ {z} n_ {x} & n_ {z} n_ {y} & n_ {z}^{2} \ end {bmatrix}}}$

men kuben ( n ⋅ K ) ³ returnerer til ( n ⋅ K ) , og som alltid den nulte kraft er 4 x 4 identitet, ( n ⋅ K ) ⁰ = I . Generelt er de odde krefter n = 1, 3, 5, ... er

${\ displaystyle (\ mathbf {n} \ cdot \ mathbf {K})^{n} = (\ mathbf {n} \ cdot \ mathbf {K})}$

mens de jevne kreftene n = 2, 4, 6, ... er

${\ displaystyle (\ mathbf {n} \ cdot \ mathbf {K})^{n} = (\ mathbf {n} \ cdot \ mathbf {K})^{2}}$

derfor avhenger den eksplisitte formen av boostmatrisen bare generatoren og kvadratet. Ved å dele kraftseriene i en merkelig kraftserie og en jevn kraftserie ved hjelp av generatorens oddetall og partall og Taylor -serien sinh ϕ og cosh ϕ om ϕ = 0 får en mer kompakt, men detaljert form for boostmatrisen

${\ displaystyle {\ begynne {justert} e^{-\ phi \ mathbf {n} \ cdot \ mathbf {K}} & =-\ sum _ {n = 1,3,5 \ ldots}^{\ infty} {\ frac {1} {n!}} \ phi ^{n} (\ mathbf {n} \ cdot \ mathbf {K}) ^{n}+\ sum _ {n = 0,2,4 \ ldots} ^{\ infty} {\ frac {1} {n!}} \ phi ^{n} (\ mathbf {n} \ cdot \ mathbf {K}) ^{n} \\ & =-\ venstre [\ phi +{\ frac {\ phi ^{3}} {3!}}+{\ frac {\ phi ^{5}} {5!}}+\ cdots \ right] (\ mathbf {n} \ cdot \ mathbf {K})+I+\ venstre [-1+1+{\ frac {1} {2!}} \ Phi ^{2}+{\ frac {1} {4!}} \ Phi ^{4}+ {\ frac {1} {6!}} \ phi ^{6}+\ cdots \ right] (\ mathbf {n} \ cdot \ mathbf {K}) ^{2} \\ & =-\ sinh \ phi (\ mathbf {n} \ cdot \ mathbf {K})+I+(-1+ \ cosh \ phi) (\ mathbf {n} \ cdot \ mathbf {K})^{2} \ end {justert}}}$

der 0 = −1 + 1 introduseres for den jevne kraftserien for å fullføre Taylor -serien for kosh ϕ . Økningen ligner Rodrigues rotasjonsformel ,

${\ displaystyle B (\ mathbf {n}, \ phi) = e^{-\ phi \ mathbf {n} \ cdot \ mathbf {K}} = I- \ sinh \ phi (\ mathbf {n} \ cdot \ mathbf {K})+(\ cosh \ phi -1) (\ mathbf {n} \ cdot \ mathbf {K})^{2} \ ,.}$

Negere hastigheten i eksponentiell gir matrisen for invers transformasjon,

${\ displaystyle B (\ mathbf {n},-\ phi) = e^{\ phi \ mathbf {n} \ cdot \ mathbf {K}} = I+\ sinh \ phi (\ mathbf {n} \ cdot \ mathbf {K})+(\ cosh \ phi -1) (\ mathbf {n} \ cdot \ mathbf {K})^{2} \ ,.}$

I kvantemekanikk , relativistisk kvantemekanikk og kvantefeltteori brukes en annen konvensjon for boostgeneratorene; alle boost -generatorene multipliseres med en faktor i den imaginære enheten i = √ −1 .

Fra eksperimenter

Howard Percy Robertson og andre viste at Lorentz -transformasjonen også kan avledes empirisk. For å oppnå dette er det nødvendig å skrive ned koordinat transformasjoner som inkluderer eksperimentelt testbare parametere. La oss for eksempel gi en enkelt "foretrukket" treghetsramme der lysets hastighet er konstant, isotrop og uavhengig av kildehastigheten. Det antas også at Einstein -synkronisering og synkronisering med langsom klokketransport er likeverdige i denne rammen. Anta deretter en annen ramme i relativ bevegelse, der klokker og stenger har samme indre utforming som i den foretrukne rammen. Følgende forhold er imidlertid ikke definert: ${\ displaystyle X, Y, Z, T}$${\ displaystyle x, y, z, t}$

• ${\ displaystyle a (v)}$ forskjeller i tidsmålinger,
• ${\ displaystyle b (v)}$ forskjeller i målte lengdes lengder,
• ${\ displaystyle d (v)}$ forskjeller i målte tverrgående lengder,
• ${\ displaystyle \ varepsilon (v)}$ avhenger av klokkesynkroniseringsprosedyren i den bevegelige rammen,

deretter er transformasjonsformlene (antatt å være lineære) mellom disse rammene gitt av:

${\ displaystyle {\ begynne {justert} t & = a (v) T+\ varepsilon (v) x \\ x & = b (v) (X-vT) \\ y & = d (v) Y \\ z & = d ( v) Z \ end {align}}}$

${\ displaystyle \ varepsilon (v)}$avhenger av synkroniseringskonvensjonen og er ikke bestemt eksperimentelt, den oppnår verdien ved å bruke Einstein -synkronisering i begge rammer. Forholdet mellom og bestemmes av Michelson - Morley -eksperimentet , forholdet mellom og bestemmes av Kennedy - Thorndike -eksperimentet , og alene bestemmes av Ives - Stilwell -eksperimentet . På denne måten har de blitt bestemt med stor presisjon til og som konverterer transformasjonen ovenfor til Lorentz -transformasjonen. ${\ displaystyle -v/c^{2}}$${\ displaystyle b (v)}$${\ displaystyle d (v)}$${\ displaystyle a (v)}$${\ displaystyle b (v)}$${\ displaystyle a (v)}$${\ displaystyle 1/a (v) = b (v) = \ gamma}$${\ displaystyle d (v) = 1}$

Se også

• Lorentz -gruppen
• Noeters teorem
• Poincaré -gruppe
• Riktig tid
• Relativistisk metrisk
• Spinor

Merknader

Referanser

• Greiner, W .; Bromley, DA (2000). Relativistic Quantum Mechanics (3. utg.). springer. ISBN 9783540674573.
• Landau, LD ; Lifshitz, EM (2002) [1939]. Den klassiske feltteorien . Kurs i teoretisk fysikk. 2 (4. utg.). Butterworth - Heinemann . ISBN 0-7506-2768-9.
• Weinberg, S. (2002), The Quantum Theory of Fields , 1 , Cambridge University Press , ISBN 0-521-55001-7