Mikrokanonisk ensemble - Microcanonical ensemble

I statistisk mekanikk er det mikrokanoniske ensemblet et statistisk ensemble som representerer de mulige tilstandene til et mekanisk system hvis totale energi er nøyaktig spesifisert. Systemet antas å være isolert i den forstand at det ikke kan utveksle energi eller partikler med omgivelsene, slik at (ved bevaring av energi ) energien i systemet ikke endres med tiden.

De primære makroskopiske variablene i det mikrokanoniske ensemblet er det totale antallet partikler i systemet (symbol: $N$ ), systemets volum (symbol: $V$ ), samt den totale energien i systemet (symbol: $E$ ). Hver av disse antas å være konstant i ensemblet. Av denne grunn kalles det mikrokanoniske ensemblet noen ganger $NVE$ -ensemblet .

Enkelt sagt blir det mikrokanonisk ensemble definert ved å tilordne en lik sannsynlighet til hver microstate hvis energi er innenfor et område sentrert ved $E$ . Alle andre mikrostater får en sannsynlighet på null. Siden sannsynlighetene må legge opp til 1, er sannsynligheten $P$ den inverse av antallet mikrostater $W$ innenfor energiområdet,

{\ displaystyle P = 1/W,}

Utvalget av energien blir deretter redusert i bredde inntil den er uendelig smal, fremdeles sentrert ved $E$ . I grensen for denne prosessen oppnås det mikrokanoniske ensemblet.

Gjelder

På grunn av sin forbindelse med de grunnleggende forutsetningene om likevektsstatistikk (spesielt postulatet med a priori like sannsynligheter ), er det mikrokanoniske ensemblet en viktig konseptuell byggestein i teorien. Det regnes noen ganger som den grunnleggende fordelingen av likevektsstatistikkmekanikk. Det er også nyttig i noen numeriske applikasjoner, for eksempel molekylær dynamikk . På den annen side er de fleste ikke -private systemer matematisk tungvint å beskrive i det mikrokanoniske ensemblet, og det er også uklarheter om definisjonene av entropi og temperatur. Av disse grunnene foretrekkes ofte andre ensembler for teoretiske beregninger.

Det mikrokanoniske ensemblets anvendelighet for virkelige systemer avhenger av viktigheten av energisvingninger, som kan skyldes interaksjoner mellom systemet og dets miljø, samt ukontrollerte faktorer i forberedelsen av systemet. Vanligvis er svingninger ubetydelige hvis et system er makroskopisk stort, eller hvis det er produsert med nøyaktig kjent energi og deretter opprettholdt i nær isolasjon fra omgivelsene. I slike tilfeller er det mikrokanoniske ensemblet aktuelt. Ellers er forskjellige ensembler mer passende - for eksempel det kanoniske ensemblet (svingende energi) eller det store kanoniske ensemblet (svingende energi og partikkelenummer).

Eiendommer

Termodynamiske mengder

Det grunnleggende termodynamiske potensialet til det mikrokanoniske ensemblet er entropi . Det er minst tre mulige definisjoner, hver gitt når det gjelder fasevolumfunksjonen $v (E)$ , som teller det totale antall tilstander med energi mindre enn $E$ (se avsnittet Presise uttrykk for den matematiske definisjonen av $v$ ):

den Boltzmann entropi
${\ displaystyle S _ {\ text {B}} = k \ log W = k \ log \ left (\ omega {\ frac {dv} {dE}} \ right),}$
'volumentropien'
${\ displaystyle S_ {v} = k \ log v,}$
'overflateentropien'
${\ displaystyle S_ {s} = k \ log {\ frac {dv} {dE}} = S _ {\ text {B}}-k \ log \ omega.}$

I det mikrokanoniske ensemblet er temperaturen en avledet mengde i stedet for en ekstern kontrollparameter. Det er definert som derivatet av den valgte entropien med hensyn til energi. For eksempel kan man definere "temperaturene" $T v$ og $T s$ som følger:

{\ displaystyle 1/T_ {v} = dS_ {v}/dE,}

{\ displaystyle 1/T_ {s} = dS_ {s}/dE = dS _ {\ text {B}}/dE.}

Som entropi, er det flere måter å forstå temperatur i det mikrokanoniske ensemblet. Mer generelt er korrespondansen mellom disse ensemblebaserte definisjonene og deres termodynamiske motstykker ikke perfekt, spesielt for endelige systemer.

Det mikrokanoniske trykket og kjemiske potensialet er gitt av:

{\ displaystyle {\ frac {p} {T}} = {\ frac {\ partiell S} {\ delvis V}}; \ qquad {\ frac {\ mu} {T}} =-{\ frac {\ partiell S} {\ delvis N}}}

Faseoverganger

Under deres strenge definisjon tilsvarer faseoverganger nonanalytisk oppførsel i det termodynamiske potensialet eller dets derivater. Ved å bruke denne definisjonen kan faseoverganger i det mikrokanoniske ensemblet forekomme i systemer av alle størrelser. Dette står i kontrast til de kanoniske og storslåtte kanoniske ensembler, som faseoverganger bare kan skje i den termodynamiske grensen - altså i systemer med uendelig mange grader av frihet. Grovt sett introduserer reservoarene som definerer de kanoniske eller grand kanoniske ensemblene svingninger som "jevner ut" all ikke -analytisk oppførsel i den frie energien til endelige systemer. Denne utjevningseffekten er vanligvis ubetydelig i makroskopiske systemer, som er tilstrekkelig store til at den frie energien kan tilnærme seg ikke -analytisk oppførsel ekstremt godt. Imidlertid kan den tekniske forskjellen i ensembler være viktig i den teoretiske analysen av små systemer.

Informasjon entropi

For et gitt mekanisk system (fast $N$ , $V$ ) og et gitt område av energi, den jevne fordeling av sannsynlighet over mikro (som i mikrokanonisk ensemble) maksimeres ensemble gjennomsnittlige $-⟨log P ⟩$ .

Termodynamiske analogier

Tidlig arbeid i statistisk mekanikk av Ludwig Boltzmann førte til hans eponymiske entropi -ligning for et system med en gitt total energi, $S = k log W$ , hvor $W$ er antall forskjellige tilstander som systemet har tilgang til ved den energien. Boltzmann utdypet ikke for dypt hva som egentlig utgjør settet med forskjellige tilstander i et system, i tillegg til det spesielle tilfellet med en ideell gass. Dette emnet ble undersøkt til fullføring av Josiah Willard Gibbs som utviklet den generaliserte statistiske mekanikken for vilkårlige mekaniske systemer, og definerte det mikrokanoniske ensemblet beskrevet i denne artikkelen. Gibbs undersøkte nøye analogiene mellom det mikrokanoniske ensemblet og termodynamikken, spesielt hvordan de brytes ned når det gjelder systemer med få frihetsgrader. Han introduserte ytterligere to definisjoner av mikrokanonisk entropi som ikke er avhengig av $ω$ - volumet og overflateentropien beskrevet ovenfor. (Vær oppmerksom på at overflateentropien bare skiller seg fra Boltzmann -entropien ved en $ω$ -avhengig avvik.)

Volumet entropi $S v$ og tilhørende $T v$ danne en nær analogi til termodynamisk entropi og temperatur. Det er mulig å vise akkurat det

{\ displaystyle dE = T _ {\ rm {v}} dS _ {\ rm {v}}-\ langle P \ rangle dV,}

( $⟨ P ⟩$ er ensemblet midlere trykk) som forventet for den første termodynamiske loven . En lignende ligning kan bli funnet for overflaten (Boltzmann) entropi og tilhørende $T s$ , men "trykket" i denne ligningen er en komplisert mengde som ikke er relatert til gjennomsnittstrykket.

De microcanonical $T v$ og $t s$ er ikke fullt ut tilfredsstillende i deres analogi til temperatur. Utenfor den termodynamiske grensen forekommer en rekke gjenstander.

Utrivelig resultat av å kombinere to systemer : To systemer, hver beskrevet av et uavhengig mikrokanonisk ensemble, kan bringes i termisk kontakt og få lov til å likevekt til et kombinert system som også er beskrevet av et mikrokanonisk ensemble. Dessverre kan energiflyten mellom de to systemene ikke forutsies basert på de første $T$ -ene. Selv når de første $T$ -ene er like, kan det overføres energi. Videre er $T$ for kombinasjonen forskjellig fra de opprinnelige verdiene. Dette motsier intuisjonen om at temperaturen skal være en intensiv mengde, og at to systemer med like temperatur bør være upåvirket av å bringes i termisk kontakt.
Merkelig oppførsel for fåpartikkelsystemer : Mange resultater, for eksempel den mikrokanoniske ekvipartisjonssetningen, oppnår en frihet på én eller to grader når de skrives i form av $T s$ . For en liten systemer denne offset er betydelig, og så hvis vi gjør $S s$ på analog entropi, flere unntak må gjøres for systemer med bare én eller to frihetsgrader.
Falske negative temperaturer : En negativ $T s$ oppstår når tettheten av tilstander er avtagende med energi. I noen systemer er tettheten av tilstander ikke monoton i energi, og derfor kan $T s$ endre tegn flere ganger etter hvert som energien økes.

Den foretrukne løsningen på disse problemene er å unngå bruk av det mikrokanoniske ensemblet. I mange realistiske tilfeller termostateres et system til et varmebad, slik at energien ikke er nøyaktig kjent. Deretter er en mer nøyaktig beskrivelse det kanoniske ensemblet eller det store kanoniske ensemblet , som begge har fullstendig samsvar med termodynamikk.

Presise uttrykk for ensemblet

Det nøyaktige matematiske uttrykket for et statistisk ensemble avhenger av hvilken mekanikk som vurderes - kvantum eller klassisk - siden forestillingen om en "mikrostat" er vesentlig forskjellig i disse to tilfellene. I kvantemekanikk gir diagonalisering et diskret sett med mikrostater med spesifikke energier. Det klassiske mekaniske tilfellet innebærer i stedet en integral over kanonisk faserom , og størrelsen på mikrostater i faserommet kan velges noe vilkårlig.

For å konstruere det mikrokanoniske ensemblet er det nødvendig i begge typer mekanikk å først spesifisere et energiområde. I uttrykkene nedenfor vil funksjonen (en funksjon av $H$ , som når toppen med $E$ med bredden $ω$ ) bli brukt til å representere energiområdet for å inkludere tilstander. Et eksempel på denne funksjonen vil være ${\ displaystyle f ({\ tfrac {HE} {\ omega}})}$

{\ displaystyle f (x) = {\ begin {cases} 1, og \ mathrm {if} ~ | x | <{\ tfrac {1} {2}}, \\ 0 og \ mathrm {ellers.} \ avslutte {saker}}}

eller, mer jevnt,

{\ displaystyle f (x) = e^{-\ pi x^{2}}.}

Kvantemekanisk

Eksempel på mikrokanonisk ensemble for et kvantesystem som består av en partikkel i en potensiell brønn.

Plott av alle mulige tilstander av dette systemet. Tilgjengelige stasjonære tilstander vises som horisontale søyler i varierende mørke i henhold til

| ψ i (x) | 2

.

Et ensemble som bare inneholder de tilstandene innenfor et smalt energiområde. Når energibredden blir null, oppnås et mikrokanonisk ensemble (forutsatt at intervallet inneholder minst en tilstand).

Partikkelens Hamiltonian er Schrödinger -type,

Ĥ = U (x) + p 2 /2 m

(potensialet

U (x)

er avsatt som en rød kurve). Hvert panel viser et energiposisjonsplott med de forskjellige stasjonære tilstandene, sammen med et sideplot som viser fordelingen av tilstander i energi.

Et statistisk ensemble i kvantemekanikk er representert ved en tetthetsmatrise , angitt med . Det mikrokanoniske ensemblet kan skrives ved hjelp av bra -ket -notasjon , når det gjelder systemets energi -egenstater og energi -egenverdier. Gitt et komplett grunnlag for energien egenstater $|$ $ψ$ $i$ $⟩$ , indeksert av $i$ , er det mikrokanonisk ensemble ${\ displaystyle {\ hat {\ rho}}}$

{\ displaystyle {\ hat {\ rho}} = {\ frac {1} {W}} \ sum _ {i} f \ venstre ({\ tfrac {H_ {i} -E} {\ omega}} \ høyre ) | \ psi _ {i} \ rangle \ langle \ psi _ {i} |,}

der $H i$ er energiens egenverdier bestemt av (her $Ĥ$ er systemets totale energioperatør, det vil si Hamiltonian operator ). Verdien av $W$ bestemmes ved å kreve at det er en normalisert tetthetsmatrise, og så ${\ displaystyle {\ hat {H}} | \ psi _ {i} \ rangle = H_ {i} | \ psi _ {i} \ rangle}$ ${\ displaystyle {\ hat {\ rho}}}$

{\ displaystyle W = \ sum _ {i} f \ left ({\ tfrac {H_ {i} -E} {\ omega}} \ right).}

Tilstandsvolumfunksjonen (brukes til å beregne entropi) er gitt av

{\ displaystyle v (E) = \ sum _ {H_ {i} <E} 1.}

Det mikrokanoniske ensemblet defineres ved å ta grensen for tetthetsmatrisen når energibredden går til null, men en problematisk situasjon oppstår når energibredden blir mindre enn avstanden mellom energinivåer. For veldig liten energibredde eksisterer ikke ensemblet i det hele tatt for de fleste verdier av $E$ , siden ingen tilstander faller innenfor området. Når ensemblet eksisterer, inneholder det vanligvis bare en ( eller to ) tilstander, siden energinivåene i et komplekst system bare er like ved et uhell (se tilfeldig matriseteori for mer diskusjon om dette punktet). Dessuten øker tilstandsvolumfunksjonen også bare i diskrete trinn, og derfor er dens derivat bare uendelig eller null, noe som gjør det vanskelig å definere tilstandenes tetthet. Dette problemet kan løses ved ikke å ta energiområdet helt til null og glatte ut tilstandsvolumfunksjonen, men dette gjør definisjonen av ensemblet mer komplisert, siden det da blir nødvendig å spesifisere energiområdet i tillegg til andre variabler (sammen , et $NVEω$ -ensemble).

Klassisk mekanisk

Eksempel på mikrokanonisk ensemble for et klassisk system bestående av en partikkel i en potensiell brønn.

Plott av alle mulige tilstander av dette systemet. De tilgjengelige fysiske tilstandene er jevnt fordelt i faserommet, men med en ujevn energifordeling; sideplottet viser

dv / dE

.

Et ensemble begrenset til bare de statene innenfor et smalt energiområde. Dette ensemblet fremstår som et tynt skall i faserommet. Når energibredden blir null, oppnås et mikrokanonisk ensemble.

Hvert panel viser faseplass (øvre graf) og energiposisjonsrom (nedre graf). Partikkelens Hamiltonian er

H = U (x) + p 2 /2 m

, med potensialet

U (x)

vist som en rød kurve. Sideplottet viser fordelingen av tilstander i energi.

I klassisk mekanikk er et ensemble representert av en felles sannsynlighetstetthetsfunksjon $ρ (p 1,\dots p n, q 1,\dots q n)$ definert over systemets faserom . Faserommet har $n$ generaliserte koordinater kalt $q 1, ... q n$ og $n$ assosierte kanoniske momenta kalt $p 1,\dots p n$ .

Sannsynlighetstetthetsfunksjonen for det mikrokanoniske ensemblet er:

{\ displaystyle \ rho = {\ frac {1} {h^{n} C}} {\ frac {1} {W}} f ({\ tfrac {HE} {\ omega}}),}

hvor

$H$ er systemets totale energi ( Hamiltonian ), en funksjon av fasen $(p 1, ... q n)$ ,
$h$ er en vilkårlig, men forhåndsbestemt konstant med enhetene $energi \times tid$ , som angir omfanget av en mikrostat og gir riktige dimensjoner til $ρ$ .
$C$ er en korreksjonsfaktor for overregning, ofte brukt for partikkelsystemer der identiske partikler er i stand til å skifte sted med hverandre.

Igjen bestemmes verdien av $W$ ved å kreve at $ρ$ er en normalisert sannsynlighetstetthetsfunksjon:

{\ displaystyle W = \ int \ ldots \ int {\ frac {1} {h^{n} C}} f ({\ tfrac {HE} {\ omega}}) \, dp_ {1} \ ldots dq_ { n}}

Denne integralen er tatt over hele faseområdet . Tilstandsvolumfunksjonen (brukes til å beregne entropi) er definert av

{\ displaystyle v (E) = \ int \ ldots \ int _ {H <E} {\ frac {1} {h^{n} C}} \, dp_ {1} \ ldots dq_ {n}.}

Når energibredden $ω$ blir null, reduseres verdien av $W$ i forhold til $ω$ som $W = ω (dv / dE)$ .

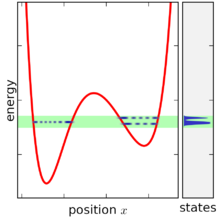
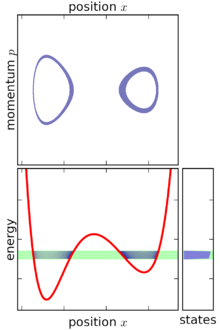
Basert på definisjonen ovenfor kan det mikrokanoniske ensemblet visualiseres som et uendelig tynt skall i faserom, sentrert på en overflate med konstant energi. Selv om det mikrokanoniske ensemblet er begrenset til denne overflaten, er det ikke nødvendigvis jevnt fordelt over denne overflaten: hvis gradienten av energi i faserommet varierer, er det mikrokanoniske ensemblet "tykkere" (mer konsentrert) i noen deler av overflaten enn andre . Denne funksjonen er en uunngåelig konsekvens av at det kreves at det mikrokanoniske ensemblet er et ensemble i steady state.

Eksempler

Ideell gass

Den grunnleggende mengden i det mikrokanoniske ensemblet er , som er lik faseromsvolumet som er kompatibelt med gitt . Fra , kan alle termodynamiske mengder beregnes. For en ideell gass er energien uavhengig av partikkelposisjonene, som derfor bidrar med en faktor til . Momenta er derimot begrenset til et -dimensjonalt (hyper-) sfærisk skall med radius ; deres bidrag er lik overflatevolumet til dette skallet. Det resulterende uttrykket for er: ${\ displaystyle W (E, V, N)}$ ${\ displaystyle (E, V, N)}$ ${\ displaystyle W}$ ${\ displaystyle V^{N}}$ ${\ displaystyle W}$ ${\ displaystyle 3N}$ ${\ displaystyle {\ sqrt {2mE}}}$ ${\ displaystyle W}$

{\ displaystyle W = {\ frac {V ^{N}} {N!}} {\ frac {2 \ pi ^{3N/2}} {\ Gamma (3N/2)}} \ venstre (2mE \ høyre )^{(3N-1)/2}}

hvor er gamma -funksjonen , og faktoren har blitt inkludert for å ta hensyn til partiklenes uskillelighet (se Gibbs paradoks ). I den store grensen, Boltzmann entropi er ${\ displaystyle \ Gamma (.)}$ ${\ displaystyle N!}$ ${\ displaystyle N}$ ${\ displaystyle S = k _ {\ mathrm {B}} \ log W}$

{\ displaystyle S = k _ {\ rm {B}} N \ log \ venstre [{\ frac {V} {N}} \ venstre ({\ frac {4 \ pi m} {3}} {\ frac {E } {N}} \ høyre)^{3/2} \ høyre]+{\ frac {5} {2}} k _ {\ rm {B}} N+O \ venstre (\ logg N \ høyre)}

Dette er også kjent som Sackur - Tetrode -ligningen .

Temperaturen er gitt av

{\ displaystyle {\ frac {1} {T}} \ equiv {\ frac {\ partiell S} {\ delvis E}} = {\ frac {3} {2}} {\ frac {Nk _ {\ mathrm {B }}} {E}}}

som stemmer overens med det analoge resultatet fra den kinetiske teorien om gasser . Beregning av trykket gir den ideelle gassloven :

{\ displaystyle {\ frac {p} {T}} \ equiv {\ frac {\ partiell S} {\ delvis V}} = {\ frac {Nk _ {\ mathrm {B}}} {V}} \ quad \ høyre pil \ quad pV = Nk _ {\ mathrm {B}} T}

Til slutt, den kjemiske potensialet er ${\ displaystyle \ mu}$

{\ displaystyle \ mu \ equiv -T {\ frac {\ partiell S} {\ delvis N}} = k _ {\ rm {B}} T \ log \ venstre [{\ frac {V} {N}} \, \ venstre ({\ frac {4 \ pi mE} {3N}} \ høyre)^{3/2} \ høyre]}

Ideell gass i et jevnt gravitasjonsfelt

Det mikrokanoniske fasevolumet kan også eksplisitt beregnes for en ideell gass i et jevnt gravitasjonsfelt .

Resultatene er angitt nedenfor for en tredimensjonal idealgass av partikler, hver med masse , begrenset i en termisk isolert beholder som er uendelig lang i z- retningen og har konstant tverrsnittsareal . Gravitasjonsfeltet antas å virke i minus z -retning med styrke . Fasevolumet er ${\ displaystyle N}$ ${\ displaystyle m}$ ${\ displaystyle A}$ ${\ displaystyle g}$ ${\ displaystyle W (E, N)}$

{\ displaystyle W (E, N) = {\ frac {(2 \ pi)^{3N/2} A^{N} m^{N/2}} {g^{N} \ Gamma (5N/2 )}} E^{{\ frac {5N} {2}}-1}}

hvor er den totale energien, kinetisk pluss gravitasjon. ${\ displaystyle E}$

Gasstettheten som funksjon av høyden kan oppnås ved å integrere over fasevolumkoordinatene. Resultatet er: ${\ displaystyle \ rho (z)}$ ${\ displaystyle z}$

{\ displaystyle \ rho (z) = \ left ({\ frac {5N} {2}}-1 \ right) {\ frac {mg} {E}} \ left (1-{\ frac {mgz} {E }} \ høyre)^{{\ frac {5N} {2}}-2}}

På samme måte er fordelingen av hastighetsstørrelsen (gjennomsnitt over alle høyder) ${\ displaystyle | {\ vec {v}} |}$

{\ displaystyle f (| {\ vec {v}} |) = {\ frac {\ Gamma (5N/2)} {\ Gamma (3/2) \ Gamma (5N/2-3/2)}}} \ ganger {\ frac {m^{3/2} | {\ vec {v}} |^{2}} {2^{1/2} E^{3/2}}} \ ganger \ igjen (1- {\ frac {m | {\ vec {v}} |^{2}} {2E}} \ høyre)^{\ frac {5 (N-1)} {2}}}

Analogene til disse ligningene i det kanoniske ensemblet er henholdsvis den barometriske formelen og Maxwell - Boltzmann -fordelingen . I grensen faller de mikrokanoniske og kanoniske uttrykkene sammen; de er imidlertid forskjellige for det endelige . Spesielt i det mikrokanoniske ensemblet er posisjonene og hastighetene ikke statistisk uavhengige. Som et resultat er den kinetiske temperaturen, definert som gjennomsnittlig kinetisk energi i et gitt volum , ujevn i hele beholderen: ${\ displaystyle N \ rightarrow \ infty}$ ${\ displaystyle N}$ ${\ displaystyle A \, dz}$

{\ displaystyle T _ {\ mathrm {kinetic}} = {\ frac {3E} {5N-2}} \ venstre (1-{\ frac {mgz} {E}} \ høyre)}

Derimot er temperaturen jevn i det kanoniske ensemblet, for enhver . ${\ displaystyle N}$

Languages

In other projects