Felt (matematikk) - Field (mathematics)

Algebraiske strukturer
Gruppe -lignende Gruppe Semigroup  / Monoid Rack and quandle Quasigroup og loop Abelsk gruppe Magma Løgngruppe Gruppeteori
ring -lignende Ringe Rng Semiring Nærring Kommutativ ring Integrert domene Felt Divisjonsring Ringteori
gitter -lignende Gitter Semilattice Komplementert gitter Total bestilling Heyting algebra Boolsk algebra Kart over gitter Gitterteori
modul -lignende Modul Gruppe med operatører Vector plass Lineær algebra
Algebra -lignende Algebra Associativ Ikke-assosiativ Sammensetning algebra Lie algebra Gradert Bialgebra
v t e

Algebraisk struktur → Ring teori Ring teori
Enkle konsepter Ringer • Subringer • Ideell • Kvotientring • Brøkdel • Total kvotering • Produktring • Gratis produkt av assosiative algebraer • Tensorprodukt av ringer Ringhomomorfismer • Kjerne • Indre automorfisme • Frobenius endomorfisme Algebraiske strukturer • Modul • Associativ algebra • Gradert ring • Involutiv ring • Kategori av ringer • Innledende ring ${\ displaystyle \ mathbb {Z}}$ • Terminalring ${\ displaystyle 0 = \ mathbb {Z} _ {1}}$ Relaterte strukturer • Felt • Endelig felt • Ikke-assosiativ ring • Lie ring • Jordan ring • Semiring • Halvfelt
Kommutativ algebra Kommutative ringer • Integrert domene • Integrert lukket domene • GCD -domene • Unikt faktoriseringsdomene • Hovedideal • Euklidisk domene • Felt • Endelig felt • Sammensetningsring • Polynomisk ring • Formell ring i kraftserien Algebraisk tallteori • Algebraisk tallfelt • Ring av heltall • Algebraisk uavhengighet • Transcendental tallteori • Transcendensgrad p -adisk tallteori og desimaler • Direkte grense / omvendt grense • Nullring ${\ displaystyle \ mathbb {Z} _ {1}}$ • Heltall modulo p n ${\ displaystyle \ mathbb {Z} /p^{n} \ mathbb {Z}}$ • Prüfer p -ring ${\ displaystyle \ mathbb {Z} (p^{\ infty})}$ • Base - p sirkel ring ${\ displaystyle \ mathbb {T}}$ • Base - p heltall ${\ displaystyle \ mathbb {Z}}$ • p -adiske begrunnelser ${\ displaystyle \ mathbb {Z} [1/s]}$ • Grunn - p reelle tall ${\ displaystyle \ mathbb {R}}$ • p -adiske heltall ${\ displaystyle \ mathbb {Z} _ {p}}$ • p -adiske tall ${\ displaystyle \ mathbb {Q} _ {p}}$ • p -adisk magnetventil ${\ displaystyle \ mathbb {T} _ {p}}$ Algebraisk geometri • Affinere variasjon
Ikke -kommutativ algebra Ikke -kommutative ringer • Divisjonsring • Semiprimitiv ring • Enkel ring • Kommutator Ikke -kommutativ algebraisk geometri Gratis algebra Clifford algebra • Geometrisk algebra Operatør algebra
v t e

I matematikk er et felt et sett der addisjon , subtraksjon , multiplikasjon og divisjon er definert og oppfører seg som de tilsvarende operasjonene på rasjonelle og reelle tall gjør. Et felt er dermed en grunnleggende algebraisk struktur som er mye brukt i algebra , tallteori og mange andre matematiske områder.

De mest kjente feltene er feltet rasjonelle tall , feltet med reelle tall og feltet med komplekse tall . Mange andre felt, for eksempel felt med rasjonelle funksjoner , algebraiske funksjonsfelt , algebraiske tallfelt og p -adiske felt, blir ofte brukt og studert i matematikk, spesielt innen tallteori og algebraisk geometri . De fleste kryptografiske protokoller er avhengige av begrensede felt , dvs. felt med uendelig mange elementer .

Forholdet mellom to felt er uttrykt ved forestillingen om en feltutvidelse . Galois -teorien , initiert av Évariste Galois på 1830 -tallet, er viet til å forstå symmetriene ved feltutvidelser. Blant andre resultater viser denne teorien at vinkeltriseksjon og kvadrering av sirkelen ikke kan gjøres med kompass og rette . Videre viser det at kvintiske ligninger generelt er algebraisk uløselige.

Felt fungerer som grunnleggende forestillinger i flere matematiske domener. Dette inkluderer forskjellige grener av matematisk analyse , som er basert på felt med tilleggsstruktur. Grunnleggende teoremer i analyse er avhengige av de strukturelle egenskapene til feltet med reelle tall. Viktigst for algebraiske formål kan et hvilket som helst felt brukes som skalarene for et vektorrom , som er den generelle standardkonteksten for lineær algebra . Tallfelt , søsken til feltet rasjonelle tall, studeres grundig i tallteori . Funksjonsfelt kan hjelpe til med å beskrive egenskapene til geometriske objekter.

Definisjon

Uformelt er et felt et sett, sammen med to operasjoner definert på det settet: en addisjonsoperasjon skrevet som a + b , og en multiplikasjonsoperasjon skrevet som a ⋅ b , som begge oppfører seg på samme måte som de oppfører seg for rasjonelle tall og reelle tall og eksistensen av et additiv invers - en for alle elementer en , og av en multiplikativ invers b ^-1 for hver ikke-null-element b . Dette gjør at man også kan vurdere de såkalte inverse operasjonene av subtraksjon , a - b og divisjon , a / b , ved å definere:

a - b = a + ( - b ) ,

a / b = a ⋅ b ⁻¹ .

Klassisk definisjon

Formelt sett er et felt et sett F sammen med to binære operasjoner på F som kalles addisjon og multiplikasjon . En binær operasjon på F er en kartlegging av F x F → F , det vil si en korrespondanse som assosieres med hvert ordnet par av elementer med F en entydig bestemt element av F . Resultatet av tillegg av a og b kalles summen av a og b , og er betegnet a + b . På samme måte kalles resultatet av multiplikasjonen av a og b produktet av a og b , og er betegnet ab eller a ⋅ b . Disse operasjonene kreves for å tilfredsstille følgende egenskaper, referert til som feltaksiomer (i disse aksiomene er a , b og c vilkårlige elementer i feltet F ):

• Tilknytning av addisjon og multiplikasjon: a + ( b + c ) = ( a + b ) + c , og a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c .
• Kommutativitet for addisjon og multiplikasjon: a + b = b + a , og a ⋅ b = b ⋅ a .
• Additiv og multiplikativ identitet : det finnes to forskjellige elementer 0 og 1 i F slik at a + 0 = a og a ⋅ 1 = a .
• Additive inverser : for hvert a i F eksisterer det et element i F , betegnet - a , kalt additiv invers av a , slik at a + ( - a ) = 0 .
• Multiplikative inverse verdier : for hver en ≠ 0 i F , eksisterer det et element i F , betegnet ved en ^-1 eller 1 / en , kalt den multiplikative inverse av et , slik at en ⋅ en ^-1 = 1 .
• Distribusjon av multiplikasjon over addisjon: a ⋅ ( b + c ) = ( a ⋅ b ) + ( a ⋅ c ) .

Dette kan oppsummeres ved å si: et felt har to operasjoner, kalt addisjon og multiplikasjon; det er en abelsk gruppe under tillegg med 0 som additiv identitet; ikke -nullelementene er en abelsk gruppe under multiplikasjon med 1 som multiplikativ identitet; og multiplikasjon fordeler seg over tillegg.

Enda mer oppsummert: et felt er en kommutativ ring der og alle ikke -nullelementer er inverterbare. ${\ displaystyle 0 \ neq 1}$

Alternativ definisjon

Felt kan også defineres på forskjellige, men likeverdige måter. Man kan alternativt definere et felt med fire binære operasjoner (addisjon, subtraksjon, multiplikasjon og divisjon) og deres nødvendige egenskaper. Divisjon med null er per definisjon ekskludert. For å unngå eksistensielle kvantifiserere kan felt defineres av to binære operasjoner (addisjon og multiplikasjon), to unære operasjoner (som gir henholdsvis additive og multiplikative inverser) og to nullary -operasjoner (konstantene 0 og 1 ). Disse operasjonene er deretter underlagt betingelsene ovenfor. Å unngå eksistensielle kvantifiserere er viktig i konstruktiv matematikk og databehandling . Man kan ekvivalent definere et felt med de samme to binære operasjonene, en unary operasjon (multiplikativ invers) og to konstanter 1 og −1 , siden 0 = 1 + (−1) og - a = (−1) a .

Eksempler

Rasjonelle tall

Rasjonelle tall har vært mye brukt lenge før utarbeidelsen av feltbegrepet. De er tall som kan skrives som brøk a / b , der a og b er heltall , og b ≠ 0 . Additiv invers av en slik brøkdel er - a / b , og multiplikativ invers (forutsatt at a ≠ 0 ) er b / a , som kan sees som følger:

${\ displaystyle {\ frac {b} {a}} \ cdot {\ frac {a} {b}} = {\ frac {ba} {ab}} = 1.}$

De abstrakt nødvendige feltaksiomene reduserer til standardegenskaper for rasjonelle tall. For eksempel kan distribusjonsloven bevises som følger:

${\ displaystyle {\ begin {align} & {\ frac {a} {b}} \ cdot \ left ({\ frac {c} {d}}+{\ frac {e} {f}} \ right) \ \ [6pt] = {} og {\ frac {a} {b}} \ cdot \ venstre ({\ frac {c} {d}} \ cdot {\ frac {f} {f}}+{\ frac { e} {f}} \ cdot {\ frac {d} {d}} \ right) \\ [6pt] = {} & {\ frac {a} {b}} \ cdot \ left ({\ frac {cf } {df}}+{\ frac {ed} {fd}} \ right) = {\ frac {a} {b}} \ cdot {\ frac {cf+ed} {df}} \\ [6pt] = {} & {\ frac {a (cf+ed)} {bdf}} = {\ frac {acf} {bdf}}+{\ frac {aed} {bdf}} = {\ frac {ac} {bd} }+{\ frac {ae} {bf}} \\ [6pt] = {} og {\ frac {a} {b}} \ cdot {\ frac {c} {d}}+{\ frac {a} {b}} \ cdot {\ frac {e} {f}}. \ end {align}}}$

Ekte og komplekse tall

De virkelige tallene R , med de vanlige addisjonene og multiplikasjonene, danner også et felt. De komplekse tallene C består av uttrykk

a + bi , med a , b ekte,

hvor i er den imaginære enheten , dvs. et (ikke-reelt) tall som tilfredsstiller i ² = −1 . Addisjon og multiplikasjon av reelle tall er definert på en slik måte at uttrykk av denne typen tilfredsstille alle felt aksiomer og dermed holde for C . For eksempel håndhever den distribuerende loven

( a + bi ) ( c + di ) = ac + bci + adi + bdi ² = ac - bd + ( bc + ad ) i .

Det er umiddelbart at dette igjen er et uttrykk for typen ovenfor, og derfor danner de komplekse tallene et felt. Komplekse tall kan bli geometrisk representert som punkter i planet , med kartesiske koordinater gitt av de reelle tallene for deres beskrivende uttrykk, eller som pilene fra opprinnelsen til disse punktene, spesifisert av lengden og en vinkel som er omsluttet av en bestemt retning. Addisjon tilsvarer da å kombinere pilene til det intuitive parallellogrammet (legge til de kartesiske koordinatene), og multiplikasjonen er - mindre intuitivt - å kombinere rotering og skalering av pilene (legge til vinklene og multiplisere lengdene). Feltene med reelle og komplekse tall brukes gjennom matematikk, fysikk, ingeniørfag, statistikk og mange andre vitenskapelige disipliner.

Konstruerbare tall

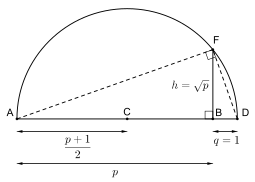
I antikken gjaldt flere geometriske problemer (in) gjennomførbarheten av å konstruere visse tall med kompass og rette . For eksempel var det ukjent for grekerne at det generelt sett er umulig å tredeling en gitt vinkel på denne måten. Disse problemene kan løses ved hjelp av feltet med konstruerbare tall . Virkelige konstruerbare tall er per definisjon lengder på linjesegmenter som kan konstrueres fra punktene 0 og 1 i uendelig mange trinn ved å bare bruke kompass og rette . Disse tallene, utstyrt med feltoperasjoner av reelle tall, begrenset til de konstruerbare tallene, danner et felt som riktig inkluderer feltet Q av rasjonelle tall. Illustrasjonen viser konstruksjonen av kvadratroten av konstruerbare tall, ikke nødvendigvis er inneholdt i Q . Bruk merkingen i illustrasjonen til å konstruere segmentene AB , BD og en halvsirkel over AD (midt på midtpunktet C ), som krysser den vinkelrette linjen gjennom B i et punkt F , i en avstand på nøyaktig fra B når BD har lengde en. ${\ displaystyle h = {\ sqrt {p}}}$

Ikke alle reelle tall er konstruerbare. Det kan vises at det ikke er et konstruerbart tall, noe som betyr at det er umulig å konstruere med kompass og rette lengden på siden av en kube med bind 2 , et annet problem som de gamle grekerne utgjør. ${\ displaystyle {\ sqrt [{3}] {2}}}$

Et felt med fire elementer

Addisjon	Multiplikasjon
+ O Jeg EN B O O Jeg EN B Jeg Jeg O B EN EN EN B O Jeg B B EN Jeg O	⋅ O Jeg EN B O O O O O Jeg O Jeg EN B EN O EN B Jeg B O B Jeg EN

I tillegg til kjente tallsystemer som rasjonene, er det andre, mindre umiddelbare eksempler på felt. Det følgende eksemplet er et felt som består av fire elementer som kalles O , I , A , og B . Notasjonen er valgt slik at O spiller rollen som det additive identitetselementet (betegnet 0 i aksiomene ovenfor), og I er den multiplikative identiteten (angitt 1 i aksiomene ovenfor). Feltaksiomene kan verifiseres ved å bruke litt mer feltteori, eller ved direkte beregning. For eksempel,

A ⋅ ( B + A ) = A ⋅ I = A , som tilsvarer A ⋅ B + A ⋅ A = I + B = A , som kreves av fordelingen.

Dette feltet kalles et begrenset felt med fire elementer, og er betegnet F ₄ eller GF (4) . Delsettet som består av O og I (markert med rødt i tabellene til høyre) er også et felt, kjent som det binære feltet F ₂ eller GF (2) . I sammenheng med informatikk og boolsk algebra er O og I ofte betegnet med henholdsvis usanne og sanne , addisjonen blir da betegnet XOR (eksklusiv eller), og multiplikasjonen er betegnet OG . Med andre ord er strukturen i det binære feltet den grunnleggende strukturen som tillater databehandling med biter .

Elementære forestillinger

I denne delen, F betegner en vilkårlig felt og en og b er vilkårlige elementer i F .

Konsekvenser av definisjonen

Den ene har en ⋅ 0 = 0 og - a = (−1) ⋅ a . Spesielt kan man utlede additiv invers av hvert element så snart man vet −1 .

Hvis ab = 0 så må a eller b være 0, siden hvis a ≠ 0 , så b = ( a ⁻¹ a ) b = a ⁻¹ ( ab ) = a ⁻¹ ⋅ 0 = 0 . Dette betyr at hvert felt er et integrert domene .

I tillegg gjelder følgende egenskaper for alle elementene a og b :

−0 = 0

1 ⁻¹ = 1

( - ( - a )) = a

( - a ) ⋅ b = a ⋅ ( - b ) = - ( a ⋅ b )

( a ⁻¹ ) ⁻¹ = a hvis a ≠ 0

Additiv og multiplikativ gruppe av et felt

Aksiomene til et felt F antyder at det er en abelsk gruppe under tillegg. Denne gruppen kalles additivgruppen i feltet, og er noen ganger betegnet med ( F , +) når den betegnes ganske enkelt som F kan være forvirrende.

På samme måte danner ikke -nullelementene i F en abelsk gruppe under multiplikasjon, kalt multiplikasjonsgruppen , og betegnet med ( F \ {0}, ⋅) eller bare F \ {0} eller F ^* .

Et felt kan dermed defineres som sett F utstyrt med to operasjoner betegnet som et tillegg og en multiplikasjon slik at F er en abelsk gruppe under tillegg, F \ {0} er en abelsk gruppe under multiplikasjon (hvor 0 er identitetselementet til tillegg), og multiplikasjon er fordelende fremfor tillegg. Noen elementære utsagn om felt kan derfor oppnås ved å bruke generelle fakta om grupper . For eksempel kan de additive og multiplikative inverse - a og a ^-1 blir entydig bestemt av en .

Kravet 1 ≠ 0 følger, fordi 1 er identitetselementet til en gruppe som ikke inneholder 0. Dermed er ikke trivialringen , som består av et enkelt element, et felt.

Hver endelige undergruppe av multiplikasjonsgruppen i et felt er syklisk (se Enhetens rot § Sykliske grupper ).

Karakteristisk

I tillegg til multiplikasjonen av to elementer av F , er det mulig å definere produktet n ⋅ a av et vilkårlig element a av F med et positivt heltall n for å være n -foldsummen

a + a + ⋯ + a (som er et element av F. )

Hvis det ikke er et positivt heltall slik

n ⋅ 1 = 0 ,

da sies F å ha karakteristisk 0. For eksempel har feltet med rasjonelle tall Q karakteristisk 0 siden ingen positive heltall n er null. Ellers, hvis det er et positivt heltall n som tilfredsstiller denne ligningen, kan det minste slike positive heltallet bli vist som et primtall . Det er vanligvis betegnet med p og feltet sies å ha karakteristisk p da. For eksempel, feltet F ₄ har karakteristiske 2 siden (i notasjonen av den ovennevnte tilsetning tabellen) I + I = O .

Dersom F er karakteristisk p , deretter p ⋅ en = 0 for alle en i F . Dette innebærer at

( a + b ) ^p = a ^p + b ^p ,

siden alle andre binomiske koeffisienter som vises i binomformelen er delbare med s . Her er a ^p  : = a ⋅ a ⋅ ⋯ ⋅ a ( p faktorer) er p -th -effekten, dvs. p -foldproduktet av elementet a . Derfor Frobenius -kartet

Fr: F → F , x ⟼ x ^s

er kompatibel med addisjonen i F (og også med multiplikasjonen), og er derfor en felthomomorfisme. Eksistensen av denne homomorfismen gjør felt i karakteristiske p ganske forskjellige fra felt med karakteristisk 0.

Delfelt og primfelt

En underfelt E av et felt F er et delsett av F som er et felt med hensyn til feltoperasjoner F . Tilsvarende er E en delmengde av F som inneholder 1 , og lukkes under tillegg, multiplikasjon, additiv invers og multiplikativ invers av et element uten null. Dette betyr at en ε E , som for alt en , b ε E både en + b og en ⋅ b er i E , og det for alle en ≠ 0 i E , både - en og en / et er i E .

Felthomomorfismer er kart f : E → F mellom to felt slik at f ( e ₁ + e ₂ ) = f ( e ₁ ) + f ( e ₂ ) , f ( e ₁ e ₂ ) = f ( e ₁ ) f ( e ₂ ) , og f (1 _e ) = 1 _F , hvor e ₁ og e ₂ er vilkårlige elementer i e . Alle felthomomorfismer er injektive . Hvis f også er surjektiv , kalles det en isomorfisme (eller feltene E og F kalles isomorf).

Et felt kalles et primfelt hvis det ikke har noen riktige (dvs. strengt mindre) underfelt. Alle felt F inneholder et hovedfelt. Dersom karakteristisk for F er p (et primtall), er hovedfeltet isomorf med det endelige felt F _p innført nedenfor. Ellers prime feltet er isomorf med Q .

Endelige felt

Endelige felt (også kalt Galois -felter ) er felt med endelig mange elementer, hvis nummer også blir referert til som rekkefølgen på feltet. Ovennevnte innledningseksempel F ₄ er et felt med fire elementer. Delfeltet F ₂ er det minste feltet, fordi et felt per definisjon har minst to forskjellige elementer 1 ≠ 0 .

De enkleste endelige feltene, med førsteklasses orden, er mest direkte tilgjengelige med modulær regning . For et fast positivt heltall n betyr aritmetisk "modulo n " å arbeide med tallene

Z / n Z = {0, 1, ..., n - 1}.

Addisjonen og multiplikasjonen på dette settet gjøres ved å utføre den aktuelle operasjonen i settet Z av heltall, dividere med n og ta resten som resultat. Denne konstruksjonen gir et felt nøyaktig hvis n er et primtall . For eksempel, tar primtall n = 2 i ovennevnte felt F ₂ . For n = 4 og mer generelt, for ethvert sammensatt tall (dvs. et tall n som kan uttrykkes som et produkt n = r ⋅ s av to strengt mindre naturlige tall), er Z / n Z ikke et felt: produktet av to ikke-null elementer er null siden r ⋅ s = 0 i Z / n Z , som, som ble forklart ovenfor , forhindrer Z / n Z i å være et felt. Feltet Z / p Z med p -elementer ( p som prime) konstruert på denne måten er vanligvis betegnet med F _p .

Hvert begrenset felt F har q = p ⁿ elementer, hvor p er primtall og n ≥ 1 . Denne uttalelsen gjelder siden F kan sees på som et vektorrom over hovedfeltet. Den dimensjonen av dette vektorrommet er nødvendigvis begrenset, si n , noe som innebærer den anførte uttalelse.

Et felt med q = p ⁿ elementer kan konstrueres som splittfeltet til polynomet

f ( x ) = x ^q - x .

Et slikt delingsfelt er en forlengelse av F _p der polynomet f har q nuller. Dette betyr at f har så mange nuller som mulig siden graden av f er q . For q = 2 ² = 4 kan det kontrolleres fra sak til sak ved hjelp av multiplikasjonstabellen ovenfor at alle fire elementene i F ₄ tilfredsstiller ligningen x ⁴ = x , så de er nuller av f . I kontrast, i F ₂ , har f bare to nuller (nemlig 0 og 1), så f deler seg ikke i lineære faktorer i dette mindre feltet. Ved å gå nærmere inn på grunnleggende feltteoretiske forestillinger, kan det vises at to begrensede felt med samme rekkefølge er isomorfe. Det er derfor vanlig å snakke om det endelige feltet med q -elementer, betegnet med F _q eller GF ( q ) .

Historie

Historisk sett førte tre algebraiske disipliner til begrepet et felt: spørsmålet om løsning av polynomligninger, algebraisk tallteori og algebraisk geometri . Et første skritt mot forestillingen om et felt ble gjort i 1770 av Joseph-Louis Lagrange , som observerte at permuting nullene x ₁ , x ₂ , x ₃ av et kubisk polynom i uttrykket

( x ₁ + ωx ₂ + ω ² x ₃ ) ³

(med ω som en tredje rot av enhet ) gir bare to verdier. På denne måten forklarte Lagrange konseptuelt den klassiske løsningsmetoden til Scipione del Ferro og François Viète , som fortsetter ved å redusere en kubisk ligning for et ukjent x til en kvadratisk ligning for x ³ . Sammen med en lignende observasjon for ligninger av grad 4 , koblet Lagrange dermed det som til slutt ble begrepet felt og begrepet grupper. Vandermonde , også i 1770, og i større grad , studerte Carl Friedrich Gauss i sine Disquisitiones Arithmeticae (1801) ligningen

x ^p = 1

for en prime p og, igjen ved bruk av moderne språk, den resulterende sykliske Galois -gruppen . Gauss utledet at en vanlig p -gon kan konstrueres hvis p = 2 ^{2 k} + 1 . Basert på Lagranges arbeid, hevdet Paolo Ruffini (1799) at kvintiske ligninger (polynomligninger av grad 5) ikke kan løses algebraisk; argumentene hans var imidlertid mangelfulle. Disse hullene ble fylt av Niels Henrik Abel i 1824. Évariste Galois , i 1832, utviklet nødvendige og tilstrekkelige kriterier for at en polynomligning kan være algebraisk løselig, og dermed etablere det som er kjent som Galois -teorien i dag. Både Abel og Galois jobbet med det som i dag kalles et algebraisk tallfelt , men tenkte verken på en eksplisitt forestilling om et felt eller en gruppe.

I 1871 introduserte Richard Dedekind , for et sett med reelle eller komplekse tall som er lukket under de fire regneoperasjonene, det tyske ordet Körper , som betyr "kropp" eller "korpus" (for å foreslå en organisk lukket enhet). Det engelske uttrykket "felt" ble introdusert av Moore (1893) .

Med et felt vil vi mene hvert uendelig system av virkelige eller komplekse tall som er så lukket i seg selv og perfekt at addisjon, subtraksjon, multiplikasjon og divisjon av to av disse tallene igjen gir et nummer av systemet.

-  Richard Dedekind, 1871

I 1881 definerte Leopold Kronecker det han kalte et rasjonalitetsdomene , som er et felt av rasjonelle fraksjoner i moderne termer. Kroneckers oppfatning dekket ikke feltet med alle algebraiske tall (som er et felt i Dedekinds forstand), men på den annen side var det mer abstrakt enn Dedekinds ved at det ikke la noen spesifikk antagelse om arten av elementene i et felt. Kronecker tolket et felt som Q (π) abstrakt som det rasjonelle funksjonsfeltet Q ( X ) . Før dette var eksempler på transcendentale tall kjent siden Joseph Liouvilles arbeid i 1844, til Charles Hermite (1873) og Ferdinand von Lindemann (1882) beviste transcendensen til henholdsvis e og π .

Den første klare definisjonen av et abstrakt felt skyldes Weber (1893) . Spesielt inkluderte Heinrich Martin Webers oppfatning feltet F _s . Giuseppe Veronese (1891) studerte feltet formelle kraftserier , noe som førte til at Hensel (1904) introduserte feltet p -adiske tall. Steinitz (1910) syntetiserte kunnskapen om abstrakt feltteori akkumulert så langt. Han studerte aksiomatisk egenskapene til felt og definerte mange viktige feltteoretiske begreper. Flertallet av teoremene som er nevnt i avsnittene Galois -teorien , Konstruere felt og elementære forestillinger kan finnes i Steinitz arbeid. Artin & Schreier (1927) knyttet begrepet ordninger i et felt , og dermed analyseområdet, til rent algebraiske egenskaper. Emil Artin ombygde Galois -teorien fra 1928 til 1942, og eliminerte avhengigheten av det primitive elementsetningen .

Konstruere felt

Konstruere felt fra ringer

En kommutativ ring er et sett, utstyrt med en tilleggs- og multiplikasjonsoperasjon, som tilfredsstiller alle aksiomer i et felt, bortsett fra eksistensen av multiplikative inverser a ^-1 . For eksempel danner heltallene Z en kommutativ ring, men ikke et felt: det gjensidige av et heltall n er ikke i seg selv et heltall, med mindre n = ± 1 .

I hierarkiet av algebraiske strukturer kan felt karakteriseres som kommutative ringer R der hvert element som ikke er null er en enhet (noe som betyr at hvert element er inverterbart). Tilsvarende områder er de kommutative ringer med nettopp to distinkte ideal , (0) og R . Felt er også nettopp kommutative ringer der (0) er det eneste hovedidealet .

Gitt en kommutativ ring R , er det to måter å konstruere et felt relatert til R , det vil si to måter å modifisere R slik at alle ikke -nullelementer blir inverterbare: å danne brøkfeltet og danne restfelt. Feltet med fraksjoner av Z er Q , rasjonene, mens restfeltene til Z er de endelige feltene F _p .

Brøkfelt

Gitt et integrert domene R , er feltet for brøkene Q ( R ) bygget med brøkene til to elementer av R nøyaktig slik Q er konstruert fra heltallene. Mer presist er elementene i Q ( R ) brøkene a / b der a og b er i R , og b ≠ 0 . To brøk a / b og c / d er like hvis og bare hvis ad = bc . Operasjonen på brøkene fungerer akkurat som for rasjonelle tall. For eksempel,

${\ displaystyle {\ frac {a} {b}}+{\ frac {c} {d}} = {\ frac {ad+bc} {bd}}.}$

Det er enkelt å vise at hvis ringen er et integrert domene, danner settet av fraksjonene et felt.

Feltet F ( x ) for de rasjonelle fraksjonene over et felt (eller et integrert domene) F er feltet for brøkene til polynomringen F [ x ] . Feltet F (( x )) i Laurent -serien

${\ displaystyle \ sum _ {i = k}^{\ infty} a_ {i} x^{i} \ (k \ in \ mathbb {Z}, a_ {i} \ in F)}$

over et felt F er feltet med fraksjoner av ringen F [[ x ]] i formelle kraftserier (der k ≥ 0 ). Siden en hvilken som helst Laurent -serie er en brøkdel av en kraftserie dividert med en effekt på x (i motsetning til en vilkårlig kraftserie), er representasjonen av brøk mindre viktig i denne situasjonen.

Restfelt

I tillegg til feltet av fraksjoner som innbygging R injectively inn i et felt, kan et felt oppnås fra en kommutativ ring R ved hjelp av et surjektiv kart på et felt F . Enhver felt oppnås på denne måten er en kvotient R / m , hvor m er en maksimal ideell for R . Dersom R har bare en maksimal ideell m , er dette feltet kalles rest felt av R .

Den ideelle generert av en enkelt polynom f i polynomet ringen R = E [ X ] (over et felt E ) er maksimal hvis og bare hvis f er ureduserbar i E , dvs. hvis f ikke kan uttrykkes som produktet av to polynomer i E [ X ] av mindre grad . Dette gir et felt

F = E [ X ] / ( f ( X )).

Dette feltet F inneholder et element x (nemlig restklassen til X ) som tilfredsstiller ligningen

f ( x ) = 0 .

For eksempel, C erholdes fra R ved tilstøtende den imaginære enhet symbol i , som tilfredsstiller f ( i ) = 0 , hvor f ( x ) = x ² + 1 . Videre er f ireduserbar over R , noe som innebærer at kartet som sender et polynom f ( X ) ∊ R [ X ] til f ( i ) gir en isomorfisme

${\ displaystyle \ mathbf {R} [X]/\ venstre (X^{2} +1 \ høyre) \ {\ stackrel {\ cong} {\ longrightarrow}} \ \ mathbf {C}.}$

Konstruere felt i et større felt

Felt kan konstrueres inne i et gitt større containerfelt. Anta at gitt et felt E , og et felt F som inneholder E som et underfelt. For ethvert element x i F er det et minste underfelt av F som inneholder E og x , kalt delfeltet til F generert av x og betegnet E ( x ) . Passasjen fra E til E ( x ) er referert til av tilstøtende et element til E . Mer generelt, for et delsett S ⊂ F , er det et minimalt underfelt av F som inneholder E og S , angitt med E ( S ) .

Den compositum av to underfelt E og E ' av enkelte felt F er den minste subfield av F inneholdende både E og E'. Den compositum kan brukes til å konstruere den største delfelt av F tilfredsstille en viss egenskap, for eksempel den største delfelt av F , som er, i språket innførte nedenfor, algebraisk enn E .

Feltutvidelser

Forestillingen om et underfelt E ⊂ F kan også betraktes fra det motsatte synspunktet, ved å referere til at F er en feltutvidelse (eller bare forlengelse) av E , betegnet med

F / E ,

og les " F over E ".

Et grunnleggende datum for en feltforlengelse er graden [ F  : E ] , dvs. dimensjonen til F som et E -vektorrom. Det tilfredsstiller formelen

[ G  : E ] = [ G  : F ] [ F  : E ] .

Utvidelser hvis grad er begrenset kalles endelige utvidelser. Forlengelsene C / R og F ₄ / F ₂ er av grad 2, mens R / Q er en uendelig forlengelse.

Algebraiske utvidelser

En sentral oppfatning i studiet av feltutvidelser F / E er algebraiske elementer . Et element er algebraisk over E hvis det er roten til et polynom med koeffisienter i E , det vil si hvis det tilfredsstiller en polynomligning${\ displaystyle x \ i F}$

e _n x ⁿ + e _{n −1} x ^{n −1} + ⋯ + e ₁ x + e ₀ = 0 ,

med e _n , ..., e ₀ i E og e _n ≠ 0 . For eksempel er den imaginære enheten i i C algebraisk over R , og til og med over Q , siden den tilfredsstiller ligningen

i ² + 1 = 0 .

En feltutvidelse der hvert element i F er algebraisk over E kalles en algebraisk utvidelse . Enhver begrenset utvidelse er nødvendigvis algebraisk, slik det kan utledes av formelen ovenfor for multiplikativitet.

Delfeltet E ( x ) generert av et element x , som ovenfor, er en algebraisk forlengelse av E hvis og bare hvis x er et algebraisk element. Det vil si at hvis x er algebraisk, er alle andre elementer i E ( x ) nødvendigvis også algebraiske. Videre er graden av utvidelsen E ( x ) / E , dvs. dimensjonen til E ( x ) som et E -vektorrom, lik den minimale graden n slik at det er en polynomligning som involverer x , som ovenfor. Hvis denne graden er n , har elementene i E ( x ) formen

${\ displaystyle \ sum _ {k = 0}^{n-1} a_ {k} x^{k}, \ \ a_ {k} \ i E.}$

For eksempel er feltet Q ( i ) av gaussiske rasjonaler underfeltet til C som består av alle tallene i formen a + bi der både a og b er rasjonelle tall: summen av skjemaet i ² (og tilsvarende for høyere eksponenter) don trenger ikke vurderes her, siden a + bi + ci ² kan forenkles til a - c + bi .

Transcendensbaser

Den ovenfor nevnte felt av rasjonelle fraksjoner E ( X ) , hvor X er en ubestemt , er ikke en algebraisk forlengelse av E , siden det ikke er noen polynomisk ligning med koeffisienter i E hvis null er X . Elementer, som X , som ikke er algebraiske, kalles transcendentale . Uformelt sett ubestemmelige X og dens krefter ikke samhandler med elementer av E . En lignende konstruksjon kan utføres med et sett med ubestemte, i stedet for bare en.

Nok en gang er feltutvidelsen E ( x ) / E diskutert ovenfor et sentralt eksempel: hvis x ikke er algebraisk (dvs. x er ikke en rot av et polynom med koeffisienter i E ), så er E ( x ) isomorf til E ( X ) . Denne isomorfismen oppnås ved å erstatte x til X i rasjonelle fraksjoner.

En delmengde S av et felt F er et transcendensgrunnlag hvis det er algebraisk uavhengig (ikke tilfredsstiller noen polynomforhold) over E og hvis F er en algebraisk forlengelse av E ( S ) . Enhver feltutvidelse F / E har et transcendensgrunnlag. Dermed kan feltutvidelser deles inn i formene E ( S ) / E ( rent transcendentale utvidelser ) og algebraiske utvidelser.

Nedleggelsesoperasjoner

Et felt er algebraisk lukket hvis det ikke har noen strengt større algebraiske utvidelser eller, tilsvarende, om noen polynomligning

f _n x ⁿ + f _{n −1} x ^{n −1} + ⋯ + f ₁ x + f ₀ = 0 , med koeffisienter f _n ,…, f ₀ ∈ F , n > 0 ,

har en løsning x e F . Ved den grunnleggende teoremet om algebra , er C algebraisk lukket, dvs. at enhver polynomligning med komplekse koeffisienter har en kompleks løsning. De rasjonelle og de reelle tallene er ikke algebraisk lukket siden ligningen

x ² + 1 = 0

har ingen rasjonell eller reell løsning. Et felt som inneholder F kalles en algebraisk lukning av F hvis det er algebraisk over F (grovt sett, ikke for stort sammenlignet med F ) og er algebraisk lukket (stort nok til å inneholde løsninger av alle polynomlige ligninger).

Ved den ovenfor angitte, C er en algebraisk lukking av R . Den situasjon som den algebraiske lukkeanordningen er en begrenset utvidelse av feltet F er helt spesielt: ved artin-Schreier teorem , graden av denne forlengelse er nødvendigvis er 2, og F er elementarily tilsvarende til R . Slike felt er også kjent som virkelige lukkede felt .

Alle felt F har en algebraisk lukning, som dessuten er unik opp til (ikke-unik) isomorfisme. Det er ofte referert til som den algebraiske lukking og betegnet F . For eksempel kalles den algebraiske lukningen Q av Q feltet med algebraiske tall . Feltet F er vanligvis ganske implisitt siden konstruksjonen krever ultrafilter-lemmaet , et sett-teoretisk aksiom som er svakere enn aksiomet til valg . I denne forbindelse er den algebraiske nedleggelsen av F _q eksepsjonelt enkel. Det er foreningen av de endelige feltene som inneholder F _q (de av orden q ⁿ ). For ethvert algebraisk lukket felt F med karakteristisk 0, er den algebraiske lukkingen av feltet F (( t )) i Laurent -serien feltet til Puiseux -serien , oppnådd ved tilgrensende røtter til t .

Felt med tilleggsstruktur

Siden feltene er allestedsnærværende i matematikk og utover, har flere forbedringer av konseptet blitt tilpasset behovene til bestemte matematiske områder.

Bestilte felt

Et felt F kalles et ordnet felt hvis to elementer kan sammenlignes, slik at x + y ≥ 0 og xy ≥ 0 når x ≥ 0 og y ≥ 0 . For eksempel danner de reelle tallene et ordnet felt, med den vanlige ordningen  ≥ . Den Artin-Schreier teoremet sier at et felt kan bestilles hvis og bare hvis det er en formelt ekte felt , noe som betyr at kvadratisk likning

${\ displaystyle x_ {1}^{2}+x_ {2}^{2}+\ dots+x_ {n}^{2} = 0}$

har bare løsningen x ₁ = x ₂ = ⋯ = x _n = 0 . Settet av alle mulige ordre på et fast felt F er isomorf med settet av ring homomorfier fra Witt ringen W ( F ) av kvadratiske former enn F , til Z .

Et arkimedisk felt er et ordnet felt slik at det for hvert element finnes et begrenset uttrykk

1 + 1 + ⋯ + 1

hvis verdi er større enn det elementet, det vil si at det ikke er uendelige elementer. Tilsvarende inneholder feltet ingen uendelige tall (elementer mindre enn alle rasjonelle tall); eller, enda tilsvarende, er det felt isomorf med et delfelt av R .

Et bestilt felt er Dedekind-komplett hvis alle øvre grenser , nedre grenser (se Dedekind-kutt ) og grenser, som burde eksistere, eksisterer. Mer formelt kreves det at hver begrenset delmengde av F har minst øvre grense. Ethvert komplett felt er nødvendigvis arkimedisk, siden det i ethvert ikke-arkimedisk felt hverken er det største uendelige eller minst positive rasjonelle, hvorfra sekvensen 1/2, 1/3, 1/4, ... , hvorav hvert element er større enn hver uendelig, har ingen grense.

Siden hvert skikkelig underfelt i realene også inneholder slike hull, er R det unike komplette ordnede feltet, opp til isomorfisme. Flere grunnleggende resultater i beregning følger direkte fra denne karakteriseringen av realen.

De hyperreals R ^* danne en ordnet felt som ikke er Arkimedes. Det er en forlengelse av realene oppnådd ved å inkludere uendelige og uendelige tall. Disse er større, henholdsvis mindre enn noe reelt tall. Hyperrealene danner grunnlaget for ikke-standardisert analyse .

Topologiske felt

En annen foredling av forestillingen om et felt er et topologisk felt , der settet F er et topologisk rom , slik at alle operasjoner av feltet (tillegg, multiplikasjon, kartene a ↦ - a og a ↦ a ⁻¹ ) er kontinuerlige kart med hensyn til plassens topologi. Topologien til alle feltene som er diskutert nedenfor, er indusert fra en beregning , dvs. en funksjon

d  : F × F → R ,

som måler en avstand mellom hvilke som helst to elementer av F .

Den ferdigstillelse av F er et annet felt der, uformelt sett er det "hull" i det opprinnelige feltet F er fylt opp, hvis det er noen. For eksempel er ethvert irrasjonelt tall x , for eksempel x = √ 2 , et "gap" i begrunnelsen Q i den forstand at det er et reelt tall som kan tilnærmes vilkårlig tett av rasjonelle tall p / q , i den forstand at avstanden til x og p / q gitt av den absolutte verdien | x - p / q | er så liten som ønsket. Tabellen nedenfor viser noen eksempler på denne konstruksjonen. Den fjerde kolonnen viser et eksempel på en null- sekvens , dvs. en sekvens som grense (for n → ∞ ) er null.

Felt	Metrisk	Fullføring	null sekvens
Sp	| x - y | (vanlig absolutt verdi )	R	1/ n
Sp	oppnådd ved hjelp av den p -adiske verdsettelsen , for et primtall p	Q p ( p -adiske tall )	p n
F ( t ) ( F et hvilket som helst felt)	oppnådd ved hjelp av den t -adiske verdivurderingen	F (( t ))	t n

Feltet Q _p brukes i tallteori og p -adisk analyse . Den algebraiske lukningen Q _p bærer en unik norm som strekker seg på Q _p , men er ikke fullstendig. Fullføringen av denne algebraiske nedleggelsen er imidlertid algebraisk lukket. På grunn av sin grove analogi til de komplekse tallene, kalles det noen ganger feltet Metriske fullføringer og algebraiske nedleggelser | komplekse p-adiske tall og er betegnet med C _p .

Lokale felt

Følgende topologiske felt kalles lokale felt :

• begrensede utvidelser av Q _p (lokale felt med karakteristisk null)
• begrensede utvidelser av F _p (( t )) , feltet til Laurent -serien over F _p (lokale felt med karakteristisk p ).

Disse to typene lokale felt har noen grunnleggende likheter. I denne relasjonen tilsvarer elementene p ∈ Q _p og t ∈ F _p (( t )) (referert til som uniformer ) hverandre. Den første manifestasjonen av dette er på et elementært nivå: elementene i begge feltene kan uttrykkes som effektserier i uniformeren, med koeffisienter i F _p . (Siden tillegget i Q _p utføres ved bruk av bæring , noe som ikke er tilfellet i F _p (( t )) , er imidlertid disse feltene ikke isomorfe.) Følgende fakta viser at denne overfladiske likheten går mye dypere:

• Enhver første ordens uttalelse som er sann for nesten alle Q _p, er også sant for nesten alle F _p (( t )) . En anvendelse av dette er Ax-Kochen-setningen som beskriver nuller av homogene polynomer i Q _s .
• Tamelig forgrenede utvidelser av begge feltene er i tilknytning til hverandre.
• Tilstøtende vilkårlige p -kraftrøtter til p (i Q _p ), henholdsvis til t (i F _p (( t )) ), gir (uendelige) utvidelser av disse feltene kjent som perfektoidfelt . Påfallende nok er Galois -gruppene i disse to feltene isomorfe, som er det første glimt av en bemerkelsesverdig parallell mellom disse to feltene:
  $${\ displaystyle \ operatorname {Gal} \ left (\ mathbf {Q} _ {p} \ left (p^{1/p^{\ infty}} \ right) \ right) \ cong \ operatorname {Gal} \ left (\ mathbf {F} _ {p} ((t)) \ venstre (t^{1/p^{\ infty}} \ høyre) \ høyre).}$$

  

Differensielle felt

Differensialfelt er felt utstyrt med en avledning , dvs. tillate å ta derivater av elementer i feltet. For eksempel danner feltet R ( X ) sammen med standardderivatet av polynomer et differensialfelt. Disse feltene er sentrale i differensial Galois -teori , en variant av Galois -teorien som omhandler lineære differensialligninger .

Galois teori

Galois -teorien studerer algebraiske utvidelser av et felt ved å studere symmetrien i de aritmetiske operasjonene addisjon og multiplikasjon. En viktig oppfatning på dette området er begrepet endelige Galois -utvidelser F / E , som per definisjon er de som kan skilles og er normale . Den primitive elementsetningen viser at endelige, separerbare utvidelser nødvendigvis er enkle , dvs. av formen

F = E [ X ] / f  ( X ) ,

hvor f er et ureduserbart polynom (som ovenfor). For en slik utvidelse betyr det å være normal og separerbar at alle nuller av f er inneholdt i F og at f bare har enkle nuller. Sistnevnte betingelse er alltid oppfylt hvis E har karakteristisk 0.

For en endelig Galois -forlengelse er Galois -gruppen Gal ( F / E ) gruppen av feltautomorfismer av F som er trivielle på E (dvs. bijeksjonene σ  : F → F som bevarer tillegg og multiplikasjon og som sender elementer av E til dem selv). Betydningen av denne gruppe stammer fra fundamentalteoremet av Galois teori , som konstruerer en eksplisitt en-til-en korrespondanse mellom et sett av undergrupper av Gal ( F / E ) og settet med mellomliggende forlengelser av forlengelsen F / E . Ved hjelp av denne korrespondansen oversettes gruppeteoretiske egenskaper til fakta om felt. For eksempel, hvis Galois -gruppen til en Galois -forlengelse som ovenfor ikke er løsbar (kan ikke bygges fra abelske grupper ), kan nullene til f ikke uttrykkes i form av tillegg, multiplikasjon og radikaler, dvs. uttrykk som involverer . For eksempel er de symmetriske gruppene S _n ikke løselige for n ≥ 5 . Følgelig, som det kan vises, er nullene til de følgende polynomene ikke uttrykkelige ved summer, produkter og radikaler. For sistnevnte polynom er dette faktum kjent som Abel - Ruffini -setningen : ${\ displaystyle {\ sqrt [{n}] {\}}}$

f ( X ) = X ⁵ - 4 X + 2 (og E = Q ),

f ( X ) = X ⁿ + en _{n -1} X ^{n -1} + + ⋯ en ₀ (hvor f er å anse som et polynom i E ( en ₀ , ..., en _{n -1} ) , for noen indeterminates en _i , E er et hvilket som helst felt, og n ≥ 5 ).

Den tensor produkt av felt er vanligvis ikke et felt. For eksempel er en endelig forlengelse F / E av grad n en Galois -forlengelse hvis og bare hvis det er en isomorfisme av F -algebraer

F ⊗ _E F ≅ F ⁿ .

Dette faktum er begynnelsen på Grothendiecks Galois-teori , en vidtrekkende forlengelse av Galois-teorien som gjelder for algebro-geometriske objekter.

Varianter av felt

Grunnleggende invarianter av et felt F inkluderer karakteristikken og transcendensgraden av F over hovedfeltet. Sistnevnte er definert som det maksimale antallet elementer i F som er algebraisk uavhengige over primfeltet. To algebraisk lukkede felt E og F er isomorfe nøyaktig hvis disse to dataene stemmer overens. Dette innebærer at to utallige algebraisk lukkede felt med samme kardinalitet og samme karakteristikk er isomorfe. For eksempel er Q _p , C _p og C isomorfe (men ikke isomorfe som topologiske felt).

Modellteori om felt

I modellteori kalles en gren av matematisk logikk , to felt E og F elementært ekvivalent hvis hver matematisk setning som er sant for E også er sant for F og omvendt. De aktuelle matematiske utsagnene må være førsteordens setninger (som involverer 0, 1, tillegg og multiplikasjon). Et typisk eksempel, for n > 0 , n et heltall, er

φ ( E ) = "ethvert polynom av grad n i E har null i E "

Settet av slike formler for alle n uttrykker at E er algebraisk lukket. Den Lefschetz prinsippet angir at C er elementarily tilsvarer et algebraisk lukkede felt F med karakteristisk null. Videre er noen fast utsagn φ holder i C hvis og bare hvis den holder i hvilken som helst algebraisk lukkede felt av tilstrekkelig høy karakteristikk.

Hvis U er et ultrafilter på et sett I , og F _i er et felt for hvert i i I , er ultaproduktet til F _i med hensyn til U et felt. Det er betegnet med

ulim _{i → ∞} F _i ,

siden den oppfører seg på flere måter som en grense for feltene F _i : Łośs teorem sier at enhver første ordens uttalelse som gjelder for alle, men endelig mange F _i , også gjelder for ultraproduktet. Når det gjelder setningen ovenfor φ , viser dette at det er en isomorfisme

${\ displaystyle \ operatorname {ulim} _ {p \ to \ infty} {\ overline {\ mathbf {F}}} _ {p} \ cong \ mathbf {C}.}$

Ax - Kochen -setningen nevnt ovenfor følger også av dette og en isomorfisme av ultraproduktene (i begge tilfeller over alle primtalene p )

ulim _p Q _p ≅ ulim _p F _p (( t )) .

I tillegg studerer modellteorien også de logiske egenskapene til forskjellige andre typer felt, for eksempel virkelige lukkede felt eller eksponensielle felt (som er utstyrt med en eksponentiell funksjon exp: F → F ^x ).

Den absolutte Galois -gruppen

For felt som ikke er algebraisk lukket (eller ikke løsbart lukket), den absolutte Galois-gruppen Gal ( F ) er fundamentalt viktig: strekker tilfelle av endelige Galois utvidelser som er skissert ovenfor, er denne gruppen styrer alle endelige separerbare forlengelser av F . Ved elementær midler, gruppen Gal ( F _q ) kan vises å være den Prufer gruppe , den profinite fullføring av Z . Denne uttalelsen går ut på at de eneste algebraiske utvidelsene til Gal ( F _q ) er feltene Gal ( F _{q ⁿ} ) for n > 0 , og at Galois -gruppene til disse endelige utvidelsene er gitt av

Gal ( F _{q ⁿ} / F _q ) = Z / n Z .

En beskrivelse når det gjelder generatorer og relasjoner er også kjent for Galois -gruppene med p -adiske tallfelt (begrensede utvidelser av Q _p ).

Representasjoner av Galois -grupper og av beslektede grupper som Weil -gruppen er grunnleggende i mange greiner av regning, for eksempel Langlands -programmet . Den kohomologiske studien av slike representasjoner er gjort ved bruk av Galois -kohomologi . For eksempel kan Brauer -gruppen , som klassisk er definert som gruppen av sentrale enkle F -algebraer , tolkes på nytt som en Galois -kohomologigruppe, nemlig

Br ( F ) = H ² ( F , G _m ) .

K-teori

Milnor K-teori er definert som

${\ displaystyle K_ {n}^{M} (F) = F^{\ times} \ otimes \ cdots \ otimes F^{\ times}/\ left \ langle x \ otimes (1-x) \ mid x \ i F \ setminus \ {0,1 \} \ right \ rangle.}$

Den norm Resten isomorfi teorem , viste seg å være omkring 2000 av Vladimir Voevodsky vedrører denne Galois cohomology ved hjelp av en isomorfi

${\ displaystyle K_ {n}^{M} (F)/p = H^{n} (F, \ mu _ {l}^{\ otimes n}).}$

Algebraisk K-teori er relatert til gruppen av inverterbare matriser med koeffisienter det gitte feltet. For eksempel fører prosessen med å ta determinanten til en inverterbar matrise til en isomorfisme K ₁ ( F ) = F ^× . Matsumotos teorem viser at K ₂ ( F ) er enig med K ₂ ^M ( F ). I høyere grader avviker K-teorien fra Milnor K-teorien og er fortsatt vanskelig å beregne generelt.

applikasjoner

Lineær algebra og kommutativ algebra

Hvis a ≠ 0 , så er ligningen

øks = b

har en unik løsning x i et felt F , nemlig Denne umiddelbare konsekvensen av definisjonen av et felt er grunnleggende i lineær algebra . For eksempel er det en vesentlig ingrediens i eliminering av Gauss og beviset på at ethvert vektorrom har et grunnlag . ${\ displaystyle x = a^{-1} b.}$

Teorien om moduler (analog av vektorrom over ringer i stedet for felt) er mye mer komplisert, fordi ligningen ovenfor kan ha flere eller ingen løsninger. Spesielt er systemer med lineære ligninger over en ring mye vanskeligere å løse enn for felt, selv i det spesielt enkle tilfellet med ringen til heltallene. ${\ displaystyle \ mathbb {Z}}$

Endelige felt: kryptografi og kodingsteori

En mye brukt kryptografisk rutine bruker det faktum at diskret eksponentiering, dvs. databehandling

a ⁿ = a ⋅ a ⋅ ⋯ ⋅ a ( n faktorer, for et heltall n ≥ 1 )

i et (stort) begrenset felt kan F _q utføres mye mer effektivt enn den diskrete logaritmen , som er den inverse operasjonen, dvs. å bestemme løsningen n til en ligning

a ⁿ = b .

I elliptisk kurvekryptografi erstattes multiplikasjonen i et endelig felt med operasjonen med å legge til punkter på en elliptisk kurve , dvs. løsningene til en ligning av formen

y ² = x ³ + ax + b .

Endelige felt brukes også i kodingsteori og kombinatorikk .

Geometri: funksjonsfelt

Funksjoner på et passende topologisk rom X i et felt k kan legges til og multipliseres punktvis, f.eks. Er produktet av to funksjoner definert av produktet av deres verdier i domenet:

( f ⋅ g ) ( x ) = f ( x ) ⋅ g ( x ) .

Dette gjør disse funksjonene til en k - kommutativ algebra .

For å ha et felt av funksjoner, må man vurdere algebraer av funksjoner som er integrert domener . I dette tilfellet er forholdene mellom to funksjoner, dvs. uttrykk for formen

${\ displaystyle {\ frac {f (x)} {g (x)}},}$

danne et felt, kalt funksjonsfelt.

Dette skjer i to hovedtilfeller. Når X er et komplekst manifold X . I dette tilfellet vurderer man algebraen til holomorfe funksjoner , dvs. komplekse differensierbare funksjoner. Deres forhold danner feltet meromorphic funksjoner på X .

Den funksjonsfeltet av en algebraisk rekke X (et geometrisk objekt defineres som de vanlige nuller av polynomlikninger) består av forhold av vanlige funksjoner , dvs. forhold mellom polynomiske funksjoner på variasjon. Funksjonsfeltet til det n -dimensjonale rommet over et felt k er k ( x ₁ , ..., x _n ) , dvs. feltet som består av forhold mellom polynomer i n ubestemte. Funksjonsfeltet til X er det samme som det for enhver åpen tett subvariasjon. Med andre ord er funksjonsfeltet ufølsomt for å erstatte X med en (litt) mindre subvariasjon.

Funksjonsfeltet er invariant under isomorfisme og birational ekvivalens av varianter. Det er derfor et viktig verktøy for å studere abstrakte algebraiske varianter og for klassifisering av algebraiske varianter. For eksempel er dimensjonen , som tilsvarer transcendensgraden til k ( X ) , invariant under birasjonal ekvivalens. For kurver (dvs. dimensjonen er en), er funksjonsfeltet k ( X ) veldig nær X : hvis X er jevn og riktig (analog til å være kompakt ), kan X rekonstrueres, opp til isomorfisme, fra feltet av funksjoner. I høyere dimensjon funksjonsfeltet husker mindre, men likevel avgjørende informasjon om X . Studiet av funksjonsfelt og deres geometriske betydning i høyere dimensjoner omtales som birational geometri . Det minimale modellprogrammet prøver å identifisere de enkleste (i en viss presis forstand) algebraiske varianter med et foreskrevet funksjonsfelt.

Tallteori: globale felt

Globale felt er i rampelyset i algebraisk tallteori og aritmetisk geometri . De er per definisjon tallfelt (endelige utvidelser av Q ) eller funksjonsfelt over F _q (begrensede utvidelser av F _q ( t ) ). Når det gjelder lokale felt, deler disse to feltene flere lignende funksjoner, selv om de har henholdsvis karakteristisk 0 og positiv karakteristikk. Denne funksjonsfeltanalogien kan bidra til å forme matematiske forventninger, ofte først ved å forstå spørsmål om funksjonsfelt, og senere behandle tallfeltet. Det siste er ofte vanskeligere. For eksempel kan Riemann -hypotesen om nullene til Riemann zeta -funksjonen (åpen fra 2017) betraktes som parallell med Weil -antagelsene (bevist i 1974 av Pierre Deligne ).

Syklotomiske felt er blant de mest intensivt studerte tallfeltene. De er av formen Q (ζ _n ) , der ζ _n er en primitiv n -rote av enhet , dvs. et komplekst tall som tilfredsstiller ζ ⁿ = 1 og ζ ^m ≠ 1 for alle m < n . For n å være en vanlig prime , Kummer brukes cyclotomic felt for å bevise Fermats siste sats , som hevder den ikke-eksistensen av rasjonelle nonzero løsninger til ligningen

x ⁿ + y ⁿ = z ⁿ .

Lokale felt er kompletteringer av globale felt. Ostrowski teorem hevder at de eneste avslutningene av Q , et globalt felt, er det lokale felt Q _s og R . Noen ganger kan du studere regningsspørsmål i globale felt ved å se på de tilsvarende spørsmålene lokalt. Denne teknikken kalles det lokalt-globale prinsippet . For eksempel reduserer Hasse - Minkowski -setningen problemet med å finne rasjonelle løsninger for kvadratiske ligninger for å løse disse ligningene i R og Q _p , hvis løsninger lett kan beskrives.

I motsetning til for lokale felt, er ikke Galois -gruppene av globale felt kjent. Inverse Galois teori studier (uløste) problemhvorvidt en hvilken som helst endelig gruppe er Galois-gruppen Gal ( F / Q ) i et visst antall felt F . Klassefeltteori beskriver de abelske utvidelsene , det vil si de med abelsk Galois -gruppe, eller tilsvarende de abelianiserte Galois -gruppene av globale felt. En klassisk uttalelse, Kronecker - Weber teoremet , beskriver den maksimale abelske Q ^ab forlengelsen av Q : det er feltet

Q (ζ _n , n ≥ 2)

oppnådd ved å grense til alle primitive n -th enhetsrøtter. Kronecker er Jugendtraum ber om en tilsvarende eksplisitt beskrivelse av F ^ab generell tall felt F . For imaginære kvadratisk felt , , d > 0 , teorien om komplekse multiplikasjon beskriver F ^ab ved hjelp av elliptiske kurver . For generelle tallfelt er ingen slik eksplisitt beskrivelse kjent. ${\ displaystyle F = \ mathbf {Q} ({\ sqrt {-d}})}$

Relaterte forestillinger

I tillegg til den ekstra strukturen som feltene kan glede seg over, innrømmer felt forskjellige andre relaterte forestillinger. Siden i et hvilket som helst felt 0 ≠ 1 har ethvert felt minst to elementer. Likevel er det et feltkonsept med ett element , som antydes å være en grense for de endelige feltene F _p , slik p har en tendens til 1. I tillegg til delingsringer er det forskjellige andre svakere algebraiske strukturer knyttet til felt som f.eks. quasifields , nesten felt og semifields .

Det er også riktige klasser med feltstruktur, som noen ganger kalles felt , med stor F. De surrealistiske tallene danner et felt som inneholder realene, og vil være et felt bortsett fra det faktum at de er en riktig klasse, ikke et sett. De nimbers , et konsept fra spillteori , danne et slikt felt også.

Divisjonsringer

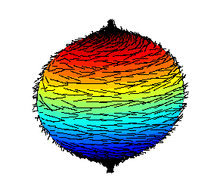
Å slippe ett eller flere aksiomer i definisjonen av et felt fører til andre algebraiske strukturer. Som nevnt ovenfor tilfredsstiller kommutative ringer alle aksiomer av felt, bortsett fra multiplikative inverser. Å droppe i stedet betingelsen om at multiplikasjon er kommutativ fører til begrepet en divisjonsring eller skjev felt . De eneste divisjonsringene som er endelige dimensjonale R- vektorrom er R selv, C (som er et felt), kvarternjonene H (der multiplikasjon er ikke-kommutativ) og oktonene O (hvor multiplikasjon verken er kommutativ eller assosiativ). Dette faktum ble bevist ved bruk av metoder for algebraisk topologi i 1958 av Michel Kervaire , Raoul Bott og John Milnor . Ikke-eksistensen av en odd-dimensjonal divisjonsalgebra er mer klassisk. Det kan utledes av den hårete ballsetningen illustrert til høyre.

Merknader

Referanser