Fermi gass - Fermi gas

Fysikk av kondensert materie
Faser  · Faseovergang  · QCP
tingenes tilstand Solid  · flytende  · Gass  · Plasma  · Bose-Einsteins kondensat  · Bose gass  · fermioniske kondensat  · Fermi gass  · Fermi væske  · Supersolid  · superflyt  · Luttinger flytende  · Tid krystall
Fasefenomener Ordre parameter  · Faseomvandlingstemperatur  · QCP
Elektroniske faser Elektronisk båndstruktur  · Plasma  · Isolator  · Mott  -isolator · Halvleder  · Halvleder  · Leder  · Superleder  · Termoelektrisk  · Piezoelektrisk  · Ferroelektrisk  · Topologisk isolator  · Spinn gapløs halvleder
Elektroniske fenomener Quantum Hall -effekt  · Spin Hall -effekt  · Kondo -effekt
Magnetiske faser Diamagnet  · Superdiamagnet Paramagnet  · Superparamagnet Ferromagnet  · Antiferromagnet Metamagnet  · Spinn glass
Kvasipartikler Phonon  · exciton  · Plasmon Polariton  · Polaron  · Magnon
Myk materie Amorft fast stoff  · Kolloid  · Granulært materiale  · Flytende krystall  · Polymer
Forskere Van der Waals  · Onnes  · von Laue  · Bragg  · Debye  · Bloch  · Onsager  · Mott  · Peierls  · Landau  · Luttinger  · Anderson  · Van Vleck  · Hubbard  · Shockley  · Bardeen  · Cooper  · Schrieffer  · Josephson  · Louis Néel  · Esaki  · Giaever  · Kohn  · Kadanoff  · Fisher  · Wilson  · von Klitzing  · Binnig  · Rohrer  · Bednorz  · Müller  · Laughlin  · Störmer  · Yang  · Tsui  · Abrikosov  · Ginzburg  · Leggett
Fysikkportal  Kategori
v t e

En ideell Fermi-gass er en tilstand av materie som er et ensemble av mange ikke-interagerende fermioner . Fermionene er partikler som lyder Fermi-Dirac statistikk , som elektroner , protoner og nøytroner , og, generelt, partikler med halv-heltall spinn . Denne statistikken bestemmer energifordelingen av fermioner i en Fermi -gass i termisk likevekt , og er preget av deres antallstetthet , temperatur og settet med tilgjengelige energitilstander. Modellen er oppkalt etter den italienske fysikeren Enrico Fermi .

Denne fysiske modellen kan brukes nøyaktig på mange systemer med mange fermioner. Noen viktige eksempler er oppførselen til ladningsbærere i et metall , nukleoner i en atomkjerne , nøytroner i en nøytronstjerne og elektroner i en hvit dverg .

Beskrivelse

Illustrasjon av energistatene: Energi-okkupasjonsdiagram for et system med 7 energinivåer, energien er degenererte tider (det er tilstander som har en energi på ) og har et belegg gitt av , med . Ved prinsippet om utelukkelse av Pauli kan opptil fermioner oppta et energinivå i systemet, hvor er fermjonenes spinn .${\ displaystyle E_ {i}}$${\ displaystyle D_ {i}}$${\ displaystyle D_ {i}}$${\ displaystyle E_ {i}}$${\ displaystyle N_ {i}}$${\ displaystyle i = 1,2,3,4,5,6,7}$${\ displaystyle (2j+1) \ cdot D_ {i}}$${\ displaystyle E_ {i}}$${\ displaystyle j}$

En ideell Fermi-gass eller fri Fermi-gass er en fysisk modell som antar en samling av ikke-interagerende fermioner i en konstant potensiell brønn . Fermions er elementære eller sammensatte partikler med halvt heltspinn , følg derfor Fermi-Dirac-statistikk . Den tilsvarende modellen for heltallspinnpartikler kalles Bose-gassen (et ensemble av ikke-interagerende bosoner ). Ved lav nok partikkelantallstetthet og høy temperatur, både på Fermi-gass og Bose gassen oppfører seg som et klassisk ideell gass .

Ved Pauli -ekskluderingsprinsippet kan ingen kvantetilstand okkuperes av mer enn en fermion med et identisk sett med kvantetall . Således konsentrerer en ikke-interagerende Fermi-gass, i motsetning til en Bose-gass, et lite antall partikler per energi. Dermed er det forbudt for en Fermi -gass å kondensere til et Bose -Einstein -kondensat , selv om svakt interagerende Fermi -gasser kan danne et Cooper -par og kondensat (også kjent som BCS -BEC crossover -regime). Den totale energien i Fermi gassen ved det absolutte nullpunkt er større enn summen av enkeltpartikkelgrunntilstander fordi Pauliprinsippet innebærer en slags interaksjon eller trykk som holder fermioner adskilt og i bevegelse. Av denne grunn er trykket til en Fermi-gass ikke-null, selv ved null temperatur, i motsetning til trykket til en klassisk idealgass. For eksempel stabiliserer dette såkalte degenerasjonstrykket en nøytronstjerne (en Fermi-gass av nøytroner) eller en hvit dvergstjerne (en Fermi-gass av elektroner) mot tyngdekraften innover , noe som tilsynelatende ville kollapse stjernen til et svart hull . Bare når en stjerne er tilstrekkelig massiv til å overvinne degenerasjonstrykket, kan den falle sammen til en egenart.

Det er mulig å definere en Fermi -temperatur under hvilken gassen kan betraktes som degenerert (trykket stammer nesten utelukkende fra Pauli -prinsippet). Denne temperaturen avhenger av massjonen til fermionene og tettheten av energitilstander .

Hovedantagelsen for den frie elektronmodellen for å beskrive de delokaliserte elektronene i et metall kan stammer fra Fermi -gassen. Siden interaksjoner blir neglisjert på grunn av screeningseffekt , reduserer problemet med å behandle likevektsegenskapene og dynamikken til en ideell Fermi -gass til studiet av oppførselen til enkeltstående uavhengige partikler. I disse systemene er Fermi -temperaturen generelt mange tusen kelvin , så i menneskelige applikasjoner kan elektrongassen betraktes som degenerert. Den maksimale energien til fermionene ved null temperatur kalles Fermi -energien . Fermi -energioverflaten i det gjensidige rommet er kjent som Fermi -overflaten .

Den nesten frie elektronmodellen tilpasser Fermi -gassmodellen for å vurdere krystallstrukturen til metaller og halvledere , hvor elektroner i et krystallgitter erstattes av Bloch -elektroner med et tilsvarende krystallmoment . Som sådan er periodiske systemer fremdeles relativt overførbare, og modellen danner utgangspunktet for mer avanserte teorier som omhandler interaksjoner, f.eks. Ved å bruke forstyrrelsesteorien .

1D uniform gass

Den endimensjonale uendelige firkantbrønnen med lengde L er en modell for en endimensjonal boks med potensiell energi:

${\ displaystyle V (x) = {\ begin {cases} 0, og x_ {c}-{\ tfrac {L} {2}} <x <x_ {c}+{\ tfrac {L} {2}}, \\\ infty, og {\ text {ellers.}} \ ende {saker}}}$

Det er et standard modellsystem i kvantemekanikk som løsningen for en enkelt partikkel er godt kjent for. Siden potensialet inne i boksen er jevnt, blir denne modellen referert til som 1D uniform gass, selv om den faktiske talltetthetsprofilen til gassen kan ha noder og antinoder når totalt antall partikler er lite.

Nivåene er merket med et enkelt kvantetall n og energiene er gitt av:

${\ displaystyle E_ {n} = E_ {0}+{\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} n ^{2}. \,}$

hvor er nullpunktsenergien (som kan velges vilkårlig som en form for målerfiksering ), massen til en enkelt fermion, og er den reduserte Planck-konstanten . ${\ displaystyle E_ {0}}$${\ displaystyle m}$${\ displaystyle \ hbar}$

For N fermioner med spin-½ i esken, kan ikke mer enn to partikler ha samme energi, dvs. to partikler kan ha energien til , to andre partikler kan ha energi og så videre. De to partiklene med samme energi har spinn ½ (spinn opp) eller ½ (spinn ned), noe som fører til to tilstander for hvert energinivå. I konfigurasjonen som den totale energien er lavest (grunntilstanden), er alle energinivåene opp til n  =  N /2 opptatt og alle de høyere nivåene er tomme. ${\ textstyle E_ {1}}$${\ textstyle E_ {2}}$

Ved å definere referansen for Fermi -energien å være , blir Fermi -energien derfor gitt av ${\ displaystyle E_ {0}}$

${\ displaystyle E _ {\ mathrm {F}} ^{({\ text {1D}})} = E_ {n} -E_ {0} = {\ frac {\ hbar ^{2} \ pi ^{2} } {2mL^{2}}} \ venstre (\ venstre \ lfloor {\ frac {N} {2}} \ høyre \ rfloor \ høyre)^{2},}$

hvor blir gulvfunksjonen evaluert til n  =  N /2. ${\ displaystyle \ left \ lfloor {\ frac {N} {2}} \ right \ rfloor}$

Termodynamisk grense

I den termodynamiske grensen er det totale antallet partikler N så stort at kvantetallet n kan behandles som en kontinuerlig variabel. I dette tilfellet er den totale talltetthetsprofilen i esken faktisk ensartet.

Antall kvantetilstander i området er: ${\ displaystyle n_ {1} <n <n_ {1}+\ operatorname {d} \! n}$

${\ displaystyle D_ {n} (n_ {1}) \ operatorname {d} \! n = 2 \ operatorname {d} \! n \ ,.}$

Uten tap av generalitet er nullpunktsenergien valgt til å være null, med følgende resultat:

${\ displaystyle E_ {n} = {\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} n ^{2} \ impliserer \ operatorname {d} \! E = { \ frac {\ hbar ^{2} \ pi ^{2}} {mL ^{2}}} n \ operatorname {d} \! n = {\ frac {\ hbar \ pi} {L}} {\ sqrt {\ frac {2E} {m}}} \ operatornavn {d} \! n \ ,.}$

Derfor i området:

${\ displaystyle E_ {1} = {\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} n_ {1} ^{2} <E <E_ {1}+\ operatornavn {d} \! E \ ,,}$

antallet kvantetilstander er:

${\ displaystyle D_ {n} (n_ {1}) \ operatorname {d} \! n = 2 {\ frac {\ operatorname {d} \! E} {\ operatorname {d} \! E/\ operatorname {d } \! n}} = {\ frac {2} {{\ frac {\ hbar ^{2} \ pi ^{2}} {ml ^{2}}} n}} \ operatorname {d} \! E \ equiv D (E_ {1}) \ operatorname {d} \! E \ ,.}$

Her er graden av degenerasjon :

${\ displaystyle D (E) = {\ frac {2} {\ operatorname {d} \! E/\ operatorname {d} \! n}} = {\ frac {2L} {\ hbar \ pi}} {\ sqrt {\ frac {m} {2E}}} \ ,.}$

Og tettheten av stater er:

${\ displaystyle g (E) \ equiv {\ frac {1} {L}} D (E) = {\ frac {2} {\ hbar \ pi}} {\ sqrt {\ frac {m} {2E}} } \ ,.}$

I moderne litteratur kalles ovennevnte noen ganger også "tetthet av stater". Skiller seg imidlertid fra med en faktor for systemets volum (som er i dette 1D -tilfellet). ${\ displaystyle D (E)}$${\ displaystyle g (E)}$${\ displaystyle D (E)}$${\ displaystyle L}$

Basert på følgende formel:

${\ displaystyle \ int _ {0}^{E_ {F}} D (E) dE = N \ ,,}$

Fermi -energien i den termodynamiske grensen kan beregnes til å være:

${\ displaystyle E _ {\ mathrm {F}} ^{({\ text {1D}})} = {\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} \ venstre ({\ frac {N} {2}} \ høyre)^{2} \ ,.}$

3D uniform gass

En modell av atomkjernen som viser den som en kompakt bunt av de to typer nukleoner : protoner (rød) og nøytroner (blå). Som en første tilnærming kan kjernen behandles som sammensatt av ikke-interagerende proton- og nøytrongasser.

Det tredimensjonale isotrope og ikke- relativistiske ensartede Fermi-gasshuset er kjent som Fermi-sfæren .

En tredimensjonal uendelig firkantet brønn, (dvs. en kubisk boks som har en sidelengde L ) har potensiell energi

${\ displaystyle V (x, y, z) = {\ begin {cases} 0, &-{\ frac {L} {2}} <x, y, z <{\ frac {L} {2}}, \\\ infty, og {\ text {ellers.}} \ ende {saker}}}$

Statene er nå merket med tre kvantetall n _x , n _y og n _z . Enkeltpartikkelenergiene er

${\ displaystyle E_ {n_ {x}, n_ {y}, n_ {z}} = E_ {0}+{\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}} } \ venstre (n_ {x}^{2}+n_ {y}^{2}+n_ {z}^{2} \ høyre) \,}$,

hvor n _x , n _y , n _z er positive heltall. I dette tilfellet har for eksempel flere stater samme energi (kjent som degenererte energinivåer ) . ${\ displaystyle E_ {211} = E_ {121} = E_ {112}}$

Termodynamisk grense

Når boksen inneholder N ikke-interagerende fermioner av spinn ½, er det interessant å beregne energien i den termodynamiske grensen, hvor N er så stor at kvantetallene n _x , n _y , n _z kan behandles som kontinuerlige variabler.

Med vektoren tilsvarer hver kvantetilstand et punkt i 'n-rom' med energi ${\ displaystyle \ mathbf {n} = (n_ {x}, n_ {y}, n_ {z})}$

${\ displaystyle E _ {\ mathbf {n}} = E_ {0}+{\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} | \ mathbf {n} | ^ {2} \,}$

Med å angi kvadratet med den vanlige euklidiske lengden . Antall tilstander med energi mindre enn E _F  +   E ₀ er lik antallet stater som ligger innenfor en radiuskule i området n-rom der n _x , n _y , n _z er positive. I grunntilstanden tilsvarer dette tallet antall fermioner i systemet: ${\ displaystyle | \ mathbf {n} |^{2}}$${\ displaystyle | \ mathbf {n} | = {\ sqrt {n_ {x}^{2}+n_ {y}^{2}+n_ {z}^{2}}}}$${\ displaystyle | \ mathbf {n} _ {\ mathrm {F}} |}$

${\ displaystyle N = 2 \ ganger {\ frac {1} {8}} \ ganger {\ frac {4} {3}} \ pi n _ {\ mathrm {F}}^{3} \,}$

De frie fermionene som opptar de laveste energitilstandene danner en sfære i det gjensidige rommet . Overflaten på denne sfæren er Fermi -overflaten .

Faktoren to uttrykker de to spinntilstandene, og faktoren 1/8 uttrykker brøkdelen av sfæren som ligger i området der alle n er positive.

${\ displaystyle n _ {\ mathrm {F}} = \ venstre ({\ frac {3N} {\ pi}} \ høyre)^{1/3}}$

Den Fermienergien er gitt ved

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} n _ {\ mathrm {F}} ^{2} = {\ frac {\ hbar ^{2} \ pi ^{2}} {2mL ^{2}}} \ venstre ({\ frac {3N} {\ pi}} \ høyre) ^{2/3}}$

Som resulterer i et forhold mellom Fermi -energien og antall partikler per volum (når L ² erstattes med V ^2/3 ):

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^{2}} {2m}} \ venstre ({\ frac {3 \ pi ^{2} N} {V}} \ høyre) ^{2/3} \,}$

Dette er også energien til partikkelen med høyest energi ( partikkelen), over nullpunktsenergien . Den th Partikkelen har en energi av ${\ displaystyle N}$${\ displaystyle E_ {0}}$${\ displaystyle N '}$

${\ displaystyle E_ {N '} = E_ {0}+{\ frac {\ hbar ^{2}} {2m}} \ venstre ({\ frac {3 \ pi ^{2} N'} {V}} \ høyre)^{2/3} \, = E_ {0}+E _ {\ mathrm {F}} {\ big |} _ {N '}}$

Den totale energien til en Fermi -sfære av fermioner (som opptar alle energitilstander i Fermisfæren) er gitt av: ${\ displaystyle N}$${\ displaystyle N}$

${\ displaystyle E _ {\ rm {T}} = NE_ {0}+\ int _ {0}^{N} E _ {\ mathrm {F}} {\ big |} _ {N^{\ prime}} \ , \ mathrm {d} N^{\ prime} = \ left ({\ frac {3} {5}} E _ {\ mathrm {F}}+E_ {0} \ right) N}$

Derfor er gjennomsnittlig energi per partikkel gitt av:

${\ displaystyle E _ {\ mathrm {av}} = E_ {0}+{\ frac {3} {5}} E _ {\ mathrm {F}}}$

Tetthet av stater

Tetthet av tilstander (DOS) for en Fermi-gass i 3-dimensjoner

For 3D-uniform Fermi-gass, med fermioner av spin-½, oppnås antall partikler som en funksjon av energien ved å erstatte Fermi-energien med en variabel energi : ${\ textstyle N (E)}$${\ textstyle (E-E_ {0})}$

${\ displaystyle N (E) = {\ frac {V} {3 \ pi ^{2}}} \ venstre [{\ frac {2m} {\ hbar ^{2}}} (E-E_ {0}) \ høyre]^{3/2}}$,

hvorfra tilstandenes tetthet (antall energitilstander per energi per volum) kan hentes. Det kan beregnes ved å differensiere antall partikler med hensyn til energien: ${\ displaystyle g (E)}$

${\ displaystyle g (E) = {\ frac {1} {V}} {\ frac {\ partiell N (E)} {\ delvis E}} = {\ frac {1} {2 \ pi ^{2} }} \ venstre ({\ frac {2m} {\ hbar ^{2}}} \ høyre) ^{3/2} {\ sqrt {E-E_ {0}}}}$.

Dette resultatet gir en alternativ måte å beregne den totale energien til en Fermi -sfære av fermioner (som opptar alle energitilstander i Fermisfæren): ${\ displaystyle N}$${\ displaystyle N}$

${\ displaystyle {\ begin {align} E_ {T} & = \ int _ {0}^{N} E \ mathrm {d} N (E) = EN (E) {\ big |} _ {0}^ {N}-\ int _ {E_ {0}}^{E_ {0}+E_ {F}} N (E) \ mathrm {d} E \\ & = (E_ {0}+E_ {F}) N- \ int _ {0}^{E_ {F}} N (E) \ mathrm {d} (E-E_ {0}) \\ & = (E_ {0}+E_ {F}) N- { \ frac {2} {5}} E_ {F} N (E_ {F}) = \ venstre (E_ {0}+{\ frac {3} {5}} E _ {\ mathrm {F}} \ høyre) N \ end {align}}}$

Termodynamiske mengder

Degenerasjonstrykk

Trykk vs temperaturkurver for klassiske og kvanteidealgasser (Fermigass, Bose -gass ) i tre dimensjoner. Pauli frastøtning i fermioner (for eksempel elektroner) gir dem et ekstra trykk over en ekvivalent klassisk gass, mest signifikant ved lav temperatur.

Ved å bruke termodynamikkens første lov kan denne indre energien uttrykkes som et trykk, det vil si

${\ displaystyle P =-{\ frac {\ partiell E _ {\ rm {T}}} {\ delvis V}} = {\ frac {2} {5}} {\ frac {N} {V}} E_ { \ mathrm {F}} = {\ frac {(3 \ pi ^{2}) ^{2/3} \ hbar ^{2}} {5m}} \ venstre ({\ frac {N} {V}} \ høyre)^{5/3},}$

hvor dette uttrykket forblir gyldig for temperaturer som er mye mindre enn Fermi -temperaturen. Dette trykket er kjent som degenerasjonstrykket . I denne forstand blir systemer sammensatt av fermioner også referert til som degenerert materie .

Standard stjernene unngå kollaps ved å balansere varme trykk ( plasma og stråling) mot gravitasjonskrefter. På slutten av stjernens levetid, når termiske prosesser er svakere, kan noen stjerner bli hvite dverger, som bare opprettholdes mot tyngdekraften av elektron degenerasjonstrykk . Ved å bruke Fermi -gassen som modell, er det mulig å beregne Chandrasekhar -grensen , dvs. maksimal masse enhver stjerne kan tilegne seg (uten vesentlig termisk generert trykk) før den kollapser i et svart hull eller en nøytronstjerne. Sistnevnte er en stjerne hovedsakelig sammensatt av nøytroner, der kollapsen også unngås ved nøytrondegenerasjonstrykk.

Når det gjelder metaller, bidrar elektrongenerasjonstrykket til materialets komprimerbarhet eller bulkmodul .

Kjemisk potensial

Forutsatt at konsentrasjonen av fermioner ikke endres med temperaturen, er det totale kjemiske potensialet µ (Fermi-nivå) til den tredimensjonale ideelle Fermi-gassen relatert til nulltemperaturen Fermi-energi E _F ved en Sommerfeld-ekspansjon (forutsatt ): ${\ displaystyle k _ {\ rm {B}} T \ ll E _ {\ mathrm {F}}}$

${\ displaystyle \ mu (T) = E_ {0}+E _ {\ mathrm {F}} \ venstre [1-{\ frac {\ pi ^{2}} {12}} \ venstre ({\ frac {k_ {\ rm {B}} T} {E _ {\ mathrm {F}}}} \ høyre) ^{2}-{\ frac {\ pi ^{4}} {80}} \ venstre ({\ frac { k _ {\ rm {B}} T} {E _ {\ mathrm {F}}}} \ right)^{4}+\ cdots \ right]}$,

hvor T er temperaturen .

Derfor er den indre kjemisk potensial , μ - E ₀ , er tilnærmet lik den Fermienergien ved temperaturer som er mye lavere enn den karakteristiske Fermi temperatur T _F . Denne karakteristiske temperaturen er i størrelsesorden 10 ⁵ K for et metall, og ved romtemperatur (300 K) er Fermi -energien og det interne kjemiske potensialet i hovedsak ekvivalente.

Typiske verdier

Metaller

Under den frie elektronmodellen kan elektronene i et metall anses å danne en jevn Fermi -gass. Antall tetthet av ledningselektroner i metaller varierer mellom omtrent 10 ²⁸ og 10 ²⁹ elektroner per m ³ , som også er den typiske tettheten av atomer i vanlig fast stoff. Denne talltettheten gir en Fermi -energi av ordenen: ${\ displaystyle N/V}$

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^{2}} {2m_ {e}}} \ venstre (3 \ pi ^{2} \ 10 ^{28 \ \ sim \ 29 } \ \ mathrm {m} ^{-3} \ right) ^{2/3} \ approx 2 \ \ sim \ 10 \ \ mathrm {eV}}$,

hvor m _e er elektronens hvilemasse . Denne Fermienergien tilsvarer et Fermi temperatur av størrelsesorden 10 ⁶ Kelvin-grader, mye høyere enn temperaturen av solen overflate. Ethvert metall vil koke før den når denne temperaturen under atmosfæretrykk. Således kan en hvilken som helst praktisk formål, kan et metall betraktes som et Fermi-gass ved null temperatur som en første tilnærmelse (normale temperaturer er liten i forhold til T _F ).

Hvite dverger

Stjerner kjent som hvite dverger har masse som kan sammenlignes med vår sol , men har omtrent en hundredel av radiusen. De høye tetthetene betyr at elektronene ikke lenger er bundet til enkeltkjerner og i stedet danner en degenerert elektrongass. Antall tetthet av elektroner i en hvit dverg er i størrelsesorden 10 ³⁶ elektroner/m ³ . Dette betyr at deres Fermi -energi er:

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^{2}} {2m_ {e}}} \ venstre ({\ frac {3 \ pi ^{2} (10 ^{36} )} {1 \ \ mathrm {m}^{3}}} \ right)^{2/3} \ ca 3 \ ganger 10^{5} \ \ mathrm {eV} = 0,3 \ \ mathrm {MeV}}$

Cellekjernen

Et annet typisk eksempel er partiklene i en atomkjerne. Kjernens radius er omtrent:

${\ displaystyle R = \ left (1,25 \ times 10^{-15} \ mathrm {m} \ right) \ times A^{1/3}}$

hvor A er antall nukleoner .

Antall tetthet av nukleoner i en kjerne er derfor:

${\ displaystyle \ rho = {\ frac {A} {{\ begin {matrise} {\ frac {4} {3}} \ end {matrise}} \ pi R^{3}}} \ ca 1,2 \ ganger 10 ^{44} \ \ mathrm {m} ^{-3}}$

Denne tettheten må deles med to, fordi Fermi -energien bare gjelder fermioner av samme type. Tilstedeværelsen av nøytroner påvirker ikke Fermi -energien til protonene i kjernen, og omvendt.

Fermi -energien til en kjerne er omtrent:

${\ displaystyle E _ {\ mathrm {F}} = {\ frac {\ hbar ^{2}} {2m _ {\ rm {p}}}}} venstre ({\ frac {3 \ pi ^{2} (6 \ ganger 10^{43})} {1 \ \ mathrm {m}^{3}}} \ høyre)^{2/3} \ ca 3 \ ganger 10^{7} \ \ mathrm {eV} = 30 \ \ mathrm {MeV}}$,

hvor m _p er protonmassen.

Kjernens radius innrømmer avvik rundt verdien nevnt ovenfor, så en typisk verdi for Fermi -energien er vanligvis gitt som 38 MeV .

Vilkårlig dimensjonal jevn gass

Tetthet av stater

Ved å bruke et volum som er integrert på dimensjoner, er tettheten av tilstander: ${\ textstyle d}$

${\ displaystyle g^{(d)} (E) = g_ {s} \ int {\ frac {\ mathrm {d}^{d} \ mathbf {k}} {(2 \ pi)^{d}} } \ delta \ venstre (E-E_ {0}-{\ frac {\ hbar ^{2} | \ mathbf {k} | ^{2}} {2m}} \ høyre) = g_ {s} \ \ venstre ({\ frac {m} {2 \ pi \ hbar^{2}}} \ høyre)^{d/2} {\ frac {(E-E_ {0})^{d/2-1}} { \ Gamma (d/2)}}}$

Fermi -energien oppnås ved å se etter antall tettheter av partikler:

${\ displaystyle \ rho = {\ frac {N} {V}} = \ int _ {E_ {0}}^{E_ {0}+E _ {\ mathrm {F}}^{(d)}} g^ {(d)} (E) \, \ mathrm {d} E}$

Å få:

${\ displaystyle E _ {\ mathrm {F}} ^{(d)} = {\ frac {2 \ pi \ hbar ^{2}} {m}} \ venstre ({\ tfrac {1} {g_ {s} }} \ Gamma \ venstre ({\ tfrac {d} {2}}+1 \ høyre) {\ frac {N} {V}} \ høyre)^{2/d}}$

hvor er det tilsvarende d -dimensjonale volumet, er dimensjonen for det indre Hilbert -rommet. For spin-½ er hver energi to ganger degenerert, så i dette tilfellet . ${\ textstyle V}$${\ textstyle g_ {s}}$${\ textstyle g_ {s} = 2}$

Et bestemt resultat oppnås for , hvor tettheten av tilstander blir en konstant (ikke avhengig av energien): ${\ displaystyle d = 2}$

${\ displaystyle g ^{(2 \ mathrm {D})} (E) = {\ frac {g_ {s}} {2}} {\ frac {m} {\ pi \ hbar ^{2}}}}$.

Fermigass i harmonisk felle

Det harmoniske fellepotensialet :

${\ displaystyle V (x, y, z) = {\ frac {1} {2}} m \ omega _ {x}^{2} x^{2}+{\ frac {1} {2}} m \ omega _ {y}^{2} y^{2}+{\ frac {1} {2}} m \ omega _ {z}^{2} z^{2}}$

er et modellsystem med mange anvendelser innen moderne fysikk. Tettheten av tilstander (eller mer nøyaktig graden av degenerasjon) for en gitt spinnart er:

${\ displaystyle g (E) = {\ frac {E^{2}} {2 (\ hbar \ omega _ {\ text {ho}})^{3}}} \ ,,}$

hvor er den harmoniske svingningsfrekvensen. ${\ displaystyle \ omega _ {\ text {ho}} = {\ sqrt [{3}] {\ omega _ {x} \ omega _ {y} \ omega _ {z}}}}}$

Fermi -energien for en gitt spinnart er:

${\ displaystyle E _ {\ rm {F}} = (6N)^{1/3} \ hbar \ omega _ {\ text {ho}} \ ,.}$

Relaterte Fermi -mengder

Relatert til Fermi -energien, forekommer også noen få nyttige mengder ofte i moderne litteratur.

Den Fermi Temperaturen er definert som , der er Boltzmanns konstant . Fermi -temperaturen kan betraktes som temperaturen der termiske effekter er sammenlignbare med kvanteeffekter forbundet med Fermi -statistikk. Fermi -temperaturen for et metall er et par størrelsesordener over romtemperatur. Andre mengder som er definert i denne sammenheng er Fermi momentum , og Fermi hastighet , som er den fart og gruppehastigheten , henholdsvis, av en fermion på Fermi overflate . Fermi -momentumet kan også beskrives som , hvor er radien til Fermi -sfæren og kalles Fermi -bølgevektoren . ${\ displaystyle T _ {\ mathrm {F}} = {\ frac {E _ {\ mathrm {F}}} {k _ {\ rm {B}}}}}}$${\ displaystyle k _ {\ rm {B}}}$ ${\ displaystyle p _ {\ mathrm {F}} = {\ sqrt {2mE _ {\ mathrm {F}}}}}}$ ${\ displaystyle v _ {\ mathrm {F}} = {\ frac {p _ {\ mathrm {F}}} {m}}}$${\ displaystyle p _ {\ mathrm {F}} = \ hbar k _ {\ mathrm {F}}}$${\ displaystyle k _ {\ mathrm {F}}}$

Vær oppmerksom på at disse mengdene ikke er veldefinerte i tilfeller der Fermi-overflaten er ikke-sfærisk.

Behandling ved endelig temperatur

Grand kanonisk ensemble

De fleste av beregningene ovenfor er nøyaktige ved null temperatur, men er fortsatt like gode tilnærminger for temperaturer lavere enn Fermi -temperaturen. For andre termodynamiske variabler er det nødvendig å skrive et termodynamisk potensial . For et ensemble av identiske fermioner er den beste måten å utlede et potensial fra det grand kanoniske ensemblet med fast temperatur, volum og kjemisk potensial µ . Årsaken skyldes Pauli -ekskluderingsprinsippet, ettersom okkupasjonstallene for hver kvantetilstand er gitt av enten 1 eller 0 (enten er det et elektron som okkuperer staten eller ikke), så (stor) partisjonsfunksjonen kan skrives som ${\ displaystyle {\ mathcal {Z}}}$

${\ displaystyle {\ mathcal {Z}} (T, V, \ mu) = \ sum _ {\ {q \}} e^{-\ beta (E_ {q}-\ mu N_ {q})}} = \ prod _ {q} \ sum _ {n_ {q} = 0}^{1} e^{-\ beta (\ varepsilon _ {q}-\ mu) n_ {q}} = \ prod _ {q} \ venstre (1+e^{-\ beta (\ varepsilon _ {q}-\ mu)} \ høyre),}$

hvor , indekserer ensembler av alle mulige mikro som gir den samme totale energi og antall partikler , er det enkelt partikkel energien til tilstand (det teller to ganger om energien av staten er degenerert) og dens belegg. Dermed er det store potensialet skrevet som ${\ displaystyle \ beta ^{-1} = k _ {\ rm {B}} T}$${\ displaystyle \ {q \}}$${\ textstyle E_ {q} = \ sum _ {q} \ varepsilon _ {q} n_ {q}}$${\ textstyle N_ {q} = \ sum _ {q} n_ {q}}$${\ textstyle \ varepsilon _ {q}}$${\ textstyle q}$${\ textstyle n_ {q} = 0,1}$

${\ displaystyle \ Omega (T, V, \ mu) =-k _ {\ rm {B}} T \ ln \ venstre ({\ mathcal {Z}} \ right) =-k _ {\ rm {B}} T \ sum _ {q} \ ln \ venstre (1+e^{\ beta (\ mu -\ varepsilon _ {q})} \ høyre)}$.

Det samme resultatet kan oppnås i det kanoniske og mikrokanoniske ensemblet , ettersom resultatet av hvert ensemble må gi samme verdi ved termodynamisk grense . Det store kanoniske ensemblet anbefales her, da det unngår bruk av kombinatorikk og faktorials . ${\ textstyle (N/V \ rightarrow \ infty)}$

Som utforsket i tidligere seksjoner, kan vi i den makroskopiske grensen bruke en kontinuerlig tilnærming (tilnærming Thomas – Fermi ) for å konvertere denne summen til en integral:

${\ displaystyle \ Omega (T, V, \ mu) =-k _ {\ rm {B}} T \ int _ {-\ infty}^{\ infty} D (\ varepsilon) \ ln (1+e^{ \ beta (\ mu -\ varepsilon)}) \, \ mathrm {d} \ varepsilon}$

hvor D ( ε ) er den totale tettheten av tilstander.

Forhold til Fermi-Dirac-distribusjon

Det store potensialet er relatert til antall partikler ved endelig temperatur på følgende måte

${\ displaystyle N =-\ left ({\ frac {\ partiell \ Omega} {\ partiell \ mu}} \ høyre) _ {T, V} = \ int _ {-\ infty}^{\ infty} D ( \ varepsilon) {\ mathcal {f}} \ left ({\ frac {\ varepsilon -\ mu} {k _ {\ rm {B}} T}} \ right) \, \ mathrm {d} \ varepsilon}$

hvor derivatet tas ved fast temperatur og volum, og det vises

${\ displaystyle {\ mathcal {f}} (x) = {\ frac {1} {e^{x} +1}}}$

også kjent som Fermi - Dirac -distribusjonen .

På samme måte er den totale interne energien

${\ displaystyle U = \ Omega -T \ venstre ({\ frac {\ partiell \ Omega} {\ delvis T}} \ høyre) _ {V, \ mu} -\ mu \ venstre ({\ frac {\ delvis \ Omega} {\ partiell \ mu}} \ høyre) _ {T, V} = \ int _ {-\ infty}^{\ infty} D (\ varepsilon) {\ mathcal {f}} \ venstre ({\ frac {\ varepsilon -\ mu} {k _ {\ rm {B}} T}} \ right) \ varepsilon \, \ mathrm {d} \ varepsilon.}$

Eksakt løsning for makt-lov-tetthet-av-stater

Entropi kontra temperaturkurver av klassisk ideell gass og kvante ideelle gasser (Fermi gass, Bose gass ) i tre dimensjoner ( α = 1,5) med konstant N , V .

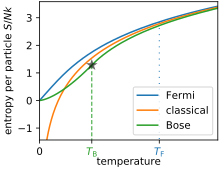
Mange interessesystemer har en total tetthet av stater med maktlovsformen:

${\ displaystyle D (\ varepsilon) = Vg (\ varepsilon) = {\ frac {Vg_ {0}} {\ Gamma (\ alpha)}} (\ varepsilon -\ varepsilon _ {0})^{\ alpha -1 }, \ qquad \ varepsilon \ geq \ varepsilon _ {0}}$

for noen verdier av g ₀ , α , ε ₀ . Resultatene fra foregående seksjoner generaliserer til d -dimensjoner, noe som gir en kraftlov med:

• α = d /2 for ikke -relativistiske partikler i en d -dimensjonal boks,
• α = d for ikke -relativistiske partikler i en d -dimensjonal harmonisk potensialbrønn,
• α = d for hyperrelativistiske partikler i en d -dimensjonal boks.

For en slik maktlovstetthet av stater, evaluerer det store potensielle integralet nøyaktig til:

${\ displaystyle \ Omega (T, V, \ mu) =-Vg_ {0} (k _ {\ rm {B}} T)^{\ alpha +1} F _ {\ alpha} \ left ({\ frac {\ mu -\ varepsilon _ {0}} {k _ {\ rm {B}} T}} \ høyre),}$

hvor er den komplette Fermi - Dirac -integralen (relatert til polylogaritmen ). Fra dette store potensialet og dets derivater kan alle termodynamiske mengder av interesse gjenvinnes. ${\ displaystyle F _ {\ alpha} (x)}$

Utvidelser til modellen

Relativistisk Fermigass

Radius-masseforhold for en modell hvit dverg, relativistisk forhold vs ikke-relativistisk. Den chandrasekhars grense er antydet som M _Ch .

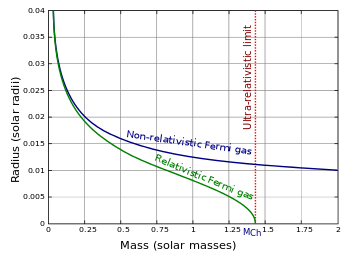
Artikkelen har bare behandlet tilfellet der partikler har et parabolsk forhold mellom energi og momentum, slik tilfellet er i ikke-relativistisk mekanikk. For partikler med energier nær deres respektive hvilemasse , er likhetene for spesiell relativitet gjeldende. Hvor enpartikkelenergi er gitt av:

${\ displaystyle E = {\ sqrt {(pc)^{2}+(mc^{2})^{2}}}}$.

For dette systemet er Fermi -energien gitt av:

${\ displaystyle E _ {\ mathrm {F}} = {\ sqrt {(p _ {\ mathrm {F}} c)^{2}+(mc^{2})^{2}}}-mc^{2 } \ ca p _ {\ mathrm {F}} c}$,

hvor likestillingen bare er gyldig i den ultrarelativistiske grensen , og ${\ displaystyle \ approx}$

${\ displaystyle p _ {\ mathrm {F}} = \ hbar \ venstre ({\ frac {1} {g_ {s}}} 6 \ pi ^{2} {\ frac {N} {V}} \ høyre) ^{1/3}}$.

Den relativistiske Fermi -gassmodellen brukes også til beskrivelse av store hvite dverger som er nær Chandresekhar -grensen. For det ultrarelativistiske tilfellet er degenerasjonstrykket proporsjonalt med . ${\ displaystyle (N/V)^{4/3}}$

Fermi væske

I 1956 utviklet Lev Landau Fermi -væsketeorien , der han behandlet tilfellet med en Fermi -væske, dvs. et system med frastøtende, ikke nødvendigvis små, interaksjoner mellom fermioner. Teorien viser at de termodynamiske egenskapene til en ideell Fermi -gass og en Fermi -væske ikke er så forskjellige. Det kan vises at Fermi -væsken tilsvarer en Fermi -gass som består av kollektive eksitasjoner eller kvasipartikler , hver med en annen effektiv masse og magnetisk moment .

Se også

• Bose gass
• Fermionisk kondensat
• Gass i en eske
• Jellium
• To-dimensjonal elektrongass

Referanser

Videre lesning

• Neil W. Ashcroft og N. David Mermin , Solid State Physics (Harcourt: Orlando, 1976).
• Charles Kittel , Introduction to Solid State Physics , 1. utg. 1953 - 8. utg. 2005, ISBN  0-471-41526-X