Quantum harmonic oscillator - Quantum harmonic oscillator

Del av en artikkelserie om
Kvantemekanikk
${\ displaystyle i \ hbar {\ frac {\ partial} {\ partiell t}} | \ psi (t) \ rangle = {\ hat {H}} | \ psi (t) \ rangle}$ Schrödinger ligning
Introduksjon Ordliste Historie
Bakgrunn Klassisk mekanikk Gammel kvanteteori Bra -ket -notasjon Hamiltonian Innblanding
Grunnleggende Komplementaritet Dekoherens Forvikling Energinivå Mål Ikke -lokalitet Kvantum Stat Superposisjon Symmetri Tunnel Usikkerhet Bølgefunksjon Kollapse
Eksperimenter Bells ulikhet Davisson - Germer Dobbel spalte Elitzur - Vaidman Franck - Hertz Leggett - Garg ulikhet Mach - Zehnder Popper Quantum viskelær Forsinket valg Schrödingers katt Stern - Gerlach Wheelers forsinkede valg
Formuleringer Oversikt Heisenberg Interaksjon Matrise Fase-plass Schrödinger Sum-over-historier (stiintegral)
Likninger Dirac Klein – Gordon Pauli Rydberg Schrödinger
Tolkninger Oversikt Bayesiansk Konsekvente historier København de Broglie – Bohm Ensemble Skjult-variabel Lokal Mange verdener Objektiv kollaps Kvantelogikk Relasjonelle Transaksjonelt
Avanserte emner Relativistisk kvantemekanikk Kvantfeltteori Kvantinformasjonsvitenskap Quantum computing Quantum kaos Tetthetsmatrise Spredningsteori Kvantestatistisk mekanikk Kvantemaskinlæring
Forskere Aharonov Klokke Blackett Bloch Bohm Bohr Født Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Pauli lam Landau Laue Moseley Millikan Onnes Planck Rabi Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

Noen baner for en harmonisk oscillator i henhold til Newtons lover om klassisk mekanikk (A – B), og i henhold til Schrödinger -ligningen for kvantemekanikk (C – H). I A – B svinger partikkelen (representert som en ball festet til en fjær ) frem og tilbake. I C – H vises noen løsninger på Schrödinger -ligningen, der den horisontale aksen er posisjon, og den vertikale aksen er den virkelige delen (blå) eller imaginær del (rød) av bølgefunksjonen . C, D, E, F, men ikke G, H, er energien egenstater . H er en sammenhengende tilstand - en kvantetilstand som tilnærmer seg den klassiske banen.

Den kvanteharmoniske oscillatoren er den kvantemekaniske analogen til den klassiske harmoniske oscillatoren . Fordi et vilkårlig jevnt potensial vanligvis kan tilnærmes som et harmonisk potensial i nærheten av et stabilt likevektspunkt , er det et av de viktigste modellsystemene innen kvantemekanikk. Videre er det et av få kvantemekaniske systemer som en eksakt, analytisk løsning er kjent for.

Endimensjonal harmonisk oscillator

Hamiltonian og energi egenstater

Bølgefunksjonsrepresentasjoner for de første åtte bundne egenstatene, n = 0 til 7. Den horisontale aksen viser posisjonen x .

Tilsvarende sannsynlighetstetthet.

Den Hamilton av partikkelen er:

${\ displaystyle {\ hat {H}} = {\ frac {{\ hat {p}}^{2}} {2m}}+{\ frac {1} {2}} k {\ hat {x}} ^{2} = {\ frac {{\ hat {p}} ^{2}} {2m}}+{\ frac {1} {2}} m \ omega ^{2} {\ hat {x}} ^{2} \ ,,}$

hvor m er partikkelmassen, k er kraftkonstanten, er oscillatorens vinkelfrekvens , er posisjonsoperatoren (gitt av x i koordinatgrunnlaget), og er momentoperatoren (gitt av i koordinatgrunnlaget). Det første uttrykket i Hamiltonian representerer den kinetiske energien til partikkelen, og det andre uttrykket representerer dens potensielle energi, som i Hookes lov . ${\ displaystyle \ omega = {\ sqrt {k/m}}}$${\ displaystyle {\ hat {x}}}$${\ displaystyle {\ hat {p}}}$${\ displaystyle {\ hat {p}} =-i \ hbar \, \ delvis /\ delvis x}$

Man kan skrive den tidsuavhengige Schrödinger-ligningen ,

${\ displaystyle {\ hat {H}} \ venstre | \ psi \ høyre \ rangle = E \ venstre | \ psi \ høyre \ rangle ~,}$

hvor E betegner et reelt tall som skal bestemmes , og som angir et tidsuavhengig energinivå , eller egenverdi , og løsningen | y ⟩ betegner det nivået energi eigenstate .

Man kan løse differensialligningen som representerer dette egenverdiproblemet i koordinatsystemet basis, for bølgefunksjonen ⟨ x | ψ ⟩ = ψ ( x ) , ved anvendelse av en spektral metode . Det viser seg at det er en familie av løsninger. På dette grunnlaget utgjør de eremittfunksjoner ,

${\ displaystyle \ psi _ {n} (x) = {\ frac {1} {\ sqrt {2^{n} \, n!}}} \ venstre ({\ frac {m \ omega} {\ pi \ hbar}} \ høyre)^{1/4} e^{-{\ frac {m \ omega x^{2}} {2 \ hbar}}} H_ {n} \ venstre ({\ sqrt {\ frac { m \ omega} {\ hbar}}} x \ right), \ qquad n = 0,1,2, \ ldots.}$

Funksjonene H _n er fysikernes eremittpolynomer ,

${\ displaystyle H_ {n} (z) = (-1)^{n} ~ e^{z^{2}} {\ frac {d^{n}} {dz^{n}}} \ venstre ( e^{-z^{2}} \ høyre).}$

De tilsvarende energinivåene er

${\ displaystyle E_ {n} = \ hbar \ omega {\ bigl (} n+{\ tfrac {1} {2}} {\ bigr)} = (2n+1) {\ hbar \ over 2} \ omega ~. }$

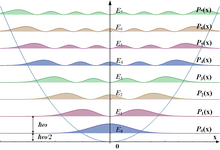
Dette energispekteret er bemerkelsesverdig av tre grunner. For det første er energiene kvantisert, noe som betyr at bare diskrete energiverdier (heltall-pluss-halv multipler av ħω ) er mulige; Dette er et generelt trekk ved kvantemekaniske systemer når en partikkel er begrenset. For det andre er disse diskrete energinivåene like store, i motsetning til Bohr -modellen av atomet, eller partikkelen i en eske . For det tredje er den lavest oppnåelige energien (energien i n = 0 -tilstanden, kalt grunntilstanden ) ikke lik minimumet til den potensielle brønnen, men ħω /2 over den; dette kalles nullpunktsenergi . På grunn av nullpunktsenergien er posisjonen og momentumet til oscillatoren i grunntilstanden ikke fast (slik de ville være i en klassisk oscillator), men har et lite variansområde, i samsvar med Heisenberg-usikkerhetsprinsippet .

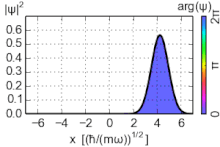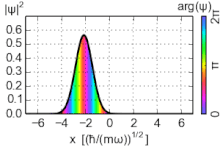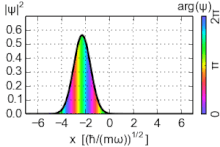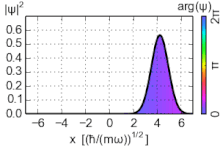
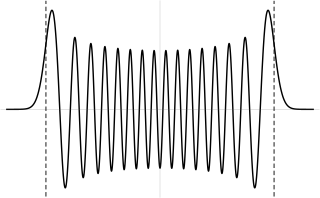
Sannsynlighetstettheten til grunnstaten er konsentrert ved opprinnelsen, noe som betyr at partikkelen tilbringer mesteparten av tiden på bunnen av den potensielle brønnen, slik man kan forvente for en tilstand med lite energi. Når energien øker, topper sannsynlighetstettheten ved de klassiske "vendepunktene", der statens energi faller sammen med den potensielle energien. (Se diskusjonen nedenfor om de svært opphissede tilstandene.) Dette er i samsvar med den klassiske harmoniske oscillatoren, der partikkelen tilbringer mer tid (og derfor er mer sannsynlig å bli funnet) nær vendepunktene, der den beveger tregest. Den korrespondanse Prinsippet er dermed oppfylt. Videre oscillerer spesielle ikke -dispersive bølgepakker , med minimal usikkerhet, kalt koherente tilstander veldig som klassiske objekter, som vist på figuren; de er ikke egenstatene til Hamiltonian.

Stigeoperatørmetode

Sannsynlighetstetthet | ψ _n ( x ) | ² for de bundne egenstatene, som begynner med grunntilstanden ( n = 0) nederst og øker i energi mot toppen. Den horisontale aksen viser posisjonen x, og lysere farger representerer høyere sannsynlighetstetthet.

" Stigeoperatør " -metoden, utviklet av Paul Dirac , tillater ekstraksjon av energiens egenverdier uten å løse differensialligningen direkte. Det er generaliserbart til mer kompliserte problemer, særlig innen kvantefeltteori . Etter denne tilnærmingen definerer vi operatørene a og tilhørende a ^† ,

${\ displaystyle {\ begin {align} a & = {\ sqrt {m \ omega \ over 2 \ hbar}} \ left ({\ hat {x}}+{i \ over m \ omega} {\ hat {p} } \ høyre) \\ a^{\ dolk} & = {\ sqrt {m \ omega \ over 2 \ hbar}} \ venstre ({\ hat {x}}-{i \ over m \ omega} {\ hat {p}} \ høyre) \ ende {justert}}}$

Dette fører til nyttig representasjon av og , ${\ displaystyle {\ hat {x}}}$${\ displaystyle {\ hat {p}}}$

${\ displaystyle {\ begin {align} {\ hat {x}} & = {\ sqrt {\ frac {\ hbar} {2m \ omega}}} (a^{\ dolk}+a) \\ {\ hat {p}} & = i {\ sqrt {\ frac {\ hbar m \ omega} {2}}} (a^{\ dolk} -a) ~. \ ende {justert}}}$

Operatøren a er ikke hermitisk , siden seg selv og tilhørende a ^† ikke er like. Energiens egenstater | n give , når den opereres av disse stigeoperatørene, gi

${\ displaystyle {\ begynne {justert} a^{\ dolk} | n \ rangle & = {\ sqrt {n+1}} | n+1 \ rangle \\ a | n \ rangle & = {\ sqrt {n }} | n-1 \ rangle. \ end {align}}}$

Det er da tydelig at en ^† i hovedsak tilfører en enkelt energikvant til oscillatoren, mens a fjerner en kvante. Av denne grunn blir de noen ganger referert til som "skapelse" og "utslettelse" -operatører.

Fra relasjonene ovenfor kan vi også definere en talloperator N , som har følgende egenskap:

${\ displaystyle {\ begynne {justert} N & = a^{\ dolk} a \\ N \ venstre | n \ høyre \ rangle & = n \ venstre | n \ høyre \ rangle. \ ende {justert}}}$

Følgende kommutatorer kan lett oppnås ved å erstatte det kanoniske kommutasjonsforholdet ,

${\ displaystyle [a, a^{\ dolk}] = 1, \ qquad [N, a^{\ dolk}] = a^{\ dolk}, \ qquad [N, a] =-a,}$

Og Hamilton -operatøren kan uttrykkes som

${\ displaystyle {\ hat {H}} = \ hbar \ omega \ venstre (N+{\ frac {1} {2}} \ høyre),}$

så egen tilstanden til N er også egen tilstanden til energi.

Pendlingseiendommen gir etter

${\ displaystyle {\ begin {align} Na^{\ dolk} | n \ rangle & = \ left (a^{\ dolk} N+[N, a^{\ dolk}] \ høyre) | n \ rangle \\ & = \ venstre (a^{\ dolk} N+a^{\ dolk} \ høyre) | n \ rangle \\ & = (n+1) a^{\ dolk} | n \ rangle, \ end {justert }}}$

og på samme måte,

${\ displaystyle Na | n \ rangle = (n-1) a | n \ rangle.}$

Dette betyr at a handler på | n ⟩ å produsere, opp til en multiplikativ konstant, | n –1⟩ , og a ^† virker på | n ⟩ for å fremstille | n +1⟩ . Av denne grunn, en kalles en utslettelse operatør ( "senke operator"), og en ^† en skapelse operatør ( "heve operator"). De to operatørene sammen kalles stigeoperatører . I kvantefeltteorien kalles a og a ^† alternativt "utslettelse" og "skapelse" -operatorer fordi de ødelegger og skaper partikler, som tilsvarer våre energikvanta.

Gitt en hvilken som helst egenenhetstilstand, kan vi handle på den med den senkende operatøren, a , for å produsere en annen egenstat med ħω mindre energi. Ved gjentatt bruk av senkende operatør ser det ut til at vi kan produsere energien egenstater ned til E = −∞ . Imidlertid siden

${\ displaystyle n = \ langle n | N | n \ rangle = \ langle n | a^{\ dolk} a | n \ rangle = {\ Bigl (} a | n \ rangle {\ Bigr)}^{\ dolk } a | n \ rangle \ geqslant 0,}$

det minste egennummeret er 0, og

${\ displaystyle a \ venstre | 0 \ høyre \ rangle = 0.}$

I dette tilfellet vil påfølgende applikasjoner av senkende operatør bare produsere null kets, i stedet for ytterligere energi -egenstater. Videre har vi vist ovenfor det

${\ displaystyle {\ hat {H}} \ venstre | 0 \ høyre \ rangle = {\ frac {\ hbar \ omega} {2}} \ venstre | 0 \ høyre \ rangle}$

Til slutt, ved å virke på | 0⟩ med operatøren for heving og multiplisere med passende normaliseringsfaktorer , kan vi produsere et uendelig sett med energi -egenstater

${\ displaystyle \ left \ {\ left | 0 \ right \ rangle, \ left | 1 \ right \ rangle, \ left | 2 \ right \ rangle, \ ldots, \ left | n \ right \ rangle, \ ldots \ right \},}$

slik at

${\ displaystyle {\ hat {H}} \ venstre | n \ høyre \ rangle = \ hbar \ omega \ venstre (n+{\ frac {1} {2}} \ høyre) \ venstre | n \ høyre \ rangle,}$

som samsvarer med energispekteret gitt i forrige seksjon.

Vilkårlige egenstater kan uttrykkes i form av | 0⟩,

${\ displaystyle | n \ rangle = {\ frac {(a^{\ dolk})^{n}} {\ sqrt {n!}}} | 0 \ rangle.}$

Bevis:

${\ displaystyle {\ begynne {justert} \ langle n | aa^{\ dolk} | n \ rangle & = \ langle n | \ venstre ([a, a^{\ dolk}]+a^{\ dolk} a \ høyre) | n \ rangle = \ langle n | (N+1) | n \ rangle = n+1 \\\ Høyre pil a^{\ dolk} | n \ rangle & = {\ sqrt {n+1}} | n+1 \ rangle \\\ Høyrepil | n \ rangle & = {\ frac {a^{\ dolk}} {\ sqrt {n}}} | n-1 \ rangle = {\ frac {(a^{ \ dolk})^{2}} {\ sqrt {n (n-1)}}} | n-2 \ rangle = \ cdots = {\ frac {(a^{\ dolk})^{n}} { \ sqrt {n!}}} | 0 \ rangle. \ end {align}}}$

Analytiske spørsmål

Den foregående analysen er algebraisk, og bruker kun kommuteringsforhold mellom operatørene for heving og senking. Når den algebraiske analysen er fullført, bør man vende seg til analytiske spørsmål. Først bør man finne grunntilstanden, det vil si løsningen på ligningen . I posisjonsrepresentasjonen er dette førsteordens differensialligning ${\ displaystyle a \ psi _ {0} = 0}$

${\ displaystyle \ left (x+{\ frac {\ hbar} {m \ omega}} {\ frac {d} {dx}} \ right) \ psi _ {0} = 0}$,

hvis løsning lett blir funnet å være Gauss

${\ displaystyle \ psi _ {0} (x) = Ce^{-{\ frac {m \ omega x^{2}} {2 \ hbar}}}}$.

Konseptuelt er det viktig at det bare er én løsning på denne ligningen; hvis det var, for eksempel, to lineært uavhengige grunntilstander, ville vi fått to uavhengige kjeder av egenvektorer for den harmoniske oscillatoren. Når grunntilstanden er beregnet, kan man induktivt vise at de opphissede tilstandene er eremittpolynomer ganger den gaussiske grunnstaten, ved å bruke den eksplisitte formen til operatøren for heving i posisjonsrepresentasjonen. Man kan også bevise at Hermite -funksjonene, som forventet fra grunntilstandens særegenhet, danner et komplett ortonormalt sett med funksjoner. ${\ displaystyle \ psi _ {n}}$

Grunntilstanden | 0⟩ i posisjonsrepresentasjonen bestemmes eksplisitt av den forrige delen, og ${\ displaystyle a | 0 \ rangle = 0}$

${\ displaystyle \ left \ langle x \ mid a \ mid 0 \ right \ rangle = 0 \ qquad \ Rightarrow \ left (x+{\ frac {\ hbar} {m \ omega}} {\ frac {d} {dx} } \ right) \ left \ langle x \ mid 0 \ right \ rangle = 0 \ qquad \ Rightarrow}$

${\ displaystyle \ left \ langle x \ mid 0 \ right \ rangle = \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right)^{\ frac {1} {4}} \ exp \ venstre (-{\ frac {m \ omega} {2 \ hbar}} x^{2} \ høyre) = \ psi _ {0} ~,}$

derav

${\ displaystyle \ langle x \ mid a^{\ dolk} \ mid 0 \ rangle = \ psi _ {1} (x) ~,}$

så det , og så videre. ${\ displaystyle \ psi _ {1} (x, t) = \ langle x \ mid e^{-3i \ omega t/2} a^{\ dolk} \ mid 0 \ rangle}$

Naturlig lengde og energivekter

Den kvanteharmoniske oscillatoren har naturlige skalaer for lengde og energi, som kan brukes til å forenkle problemet. Disse kan bli funnet ved ikke -dimensjonalisering .

Resultatet er at hvis energi måles i enheter på ħω og avstand i enheter på √ ħ /( mω ) , så forenkler Hamiltonian til

${\ displaystyle H =-{\ frac {1} {2}} {d^{2} \ over dx^{2}}+{\ frac {1} {2}} x^{2},}$

mens energiens egenfunksjoner og egenverdier forenkler til eremittfunksjoner og heltall som motvirkes med et halvt,

${\ displaystyle \ psi _ {n} (x) = \ left \ langle x \ mid n \ right \ rangle = {1 \ over {\ sqrt {2 ^{n} n!}}} ~ \ pi ^{- 1/4} \ exp (-x^{2}/2) ~ H_ {n} (x),}$

${\ displaystyle E_ {n} = n+{\ tfrac {1} {2}} ~,}$

hvor H _n ( x ) er eremittpolynomene .

For å unngå forvirring vil disse "naturlige enhetene" stort sett ikke bli vedtatt i denne artikkelen. Imidlertid kommer de ofte godt med når du utfører beregninger, ved å omgå rot.

For eksempel, den grunnleggende løsning ( utbreder ) av H-i∂ _t , den tidsavhengige Schrödinger operatør for denne oscillator, bare koker ned til Mehler kjernen ,

${\ displaystyle \ langle x \ mid \ exp (-itH) \ mid y \ rangle \ equiv K (x, y; t) = {\ frac {1} {\ sqrt {2 \ pi i \ sin t}}} \ exp \ left ({\ frac {i} {2 \ sin t}} \ left ((x^{2}+y^{2}) \ cos t-2xy \ right) \ right) ~,}$

hvor K ( x , y ; 0) = δ ( x - y ) . Den mest generelle løsningen for en gitt innledende konfigurasjon ψ ( x , 0) er da ganske enkelt

${\ displaystyle \ psi (x, t) = \ int dy ~ K (x, y; t) \ psi (y, 0) ~.}$

Sammenhengende stater

Tidsutvikling av sannsynlighetsfordelingen (og fasen, vist som farge) for en sammenhengende tilstand med | α | = 3.

De koherente tilstander på harmonisk oscillator er spesielle ikke-dispersive bølgepakker , med et minimum av usikkerhet σ _x σ _p = ℏ / 2 , som har målbare parametere ' forventningsverdier utvikle seg som et klassisk system. De er egenvektorer til utslettelsesoperatøren, ikke Hamiltonian, og danner et overkomplett grunnlag som følgelig mangler ortogonalitet.

De sammenhengende tilstandene indekseres av α ∈ ℂ og uttrykkes i | n ⟩ basis så

${\ displaystyle | \ alpha \ rangle = \ sum _ {n = 0}^{\ infty} | n \ rangle \ langle n | \ alpha \ rangle = e^{-{\ frac {1} {2}} | \ alpha |^{2}} \ sum _ {n = 0}^{\ infty} {\ frac {\ alpha^{n}} {\ sqrt {n!}}} | n \ rangle = e^{- {\ frac {1} {2}} | \ alpha |^{2}} e^{\ alpha a^{\ dolk}} e^{-{\ alpha^{*} a}} | 0 \ rangle}$.

Fordi og via Kermack-McCrae identitet, er den siste formen tilsvarer en enhetlig forskyvning operatør som virker på grunntilstanden: . De posisjon plass bølgefunksjoner er ${\ displaystyle a \ venstre | 0 \ høyre \ rangle = 0}$ ${\ displaystyle | \ alpha \ rangle = e^{\ alpha {\ hat {a}}^{\ dolk}-\ alpha^{*} {\ hat {a}}} | 0 \ rangle = D (\ alpha ) | 0 \ rangle}$

${\ displaystyle \ psi _ {\ alpha} (x ') = \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right)^{\ frac {1} {4}} e^{ {\ frac {i} {\ hbar}} \ langle {\ hat {p}} \ rangle _ {\ alpha} x '-{\ frac {m \ omega} {2 \ hbar}} (x'-\ langle {\ hat {x}} \ rangle _ {\ alpha})^{2}}}$.

Siden sammenhengende tilstander ikke er energi -egenstater, er deres tidsutvikling ikke et enkelt skifte i bølgefunksjonsfasen. De tids utviklet tilstander er imidlertid også koherente tilstander, men med faseforskyvning parameter a i stedet: . ${\ displaystyle \ alpha (t) = \ alpha (0) \ exp (-i \ omega t)}$

Svært spente stater

Bølgefunksjon (topp) og sannsynlighetstetthet (nederst) for n  = 30 eksitert tilstand for kvanteharmonisk oscillator. Loddrette stiplete linjer indikerer de klassiske vendepunktene, mens den stiplede linjen representerer den klassiske sannsynlighetstettheten.

Når n er stor, blir egentilstandene lokaliseres til den klassiske tillatte området, det vil si det område hvor en klassisk partikkel med energi E _n kan bevege seg. Egenstatene toppes nær vendepunktene: punktene i enden av det klassisk tillatte området der den klassiske partikkelen endrer retning. Dette fenomenet kan verifiseres ved asymptotikk av eremittpolynomene , og også gjennom tilnærming til WKB .

Svingningsfrekvensen ved x er proporsjonal med momentum p ( x ) til en klassisk energipartikkel E _n og posisjon x . Videre er kvadratet av amplituden (bestemmelse av sannsynlighetstettheten) omvendt proporsjonal med p ( x ) , noe som gjenspeiler hvor lang tid den klassiske partikkelen bruker nær x . Systematferden i et lite nabolag ved vendepunktet har ikke en enkel klassisk forklaring, men kan modelleres ved hjelp av en luftig funksjon . Ved å bruke egenskapene til Airy -funksjonen, kan man anslå sannsynligheten for å finne partikkelen utenfor den klassisk tillatte regionen, til å være ca.

${\ displaystyle {\ frac {2} {n^{1/3} 3^{2/3} \ Gamma^{2} ({\ tfrac {1} {3}})}} = {\ frac {1 } {n^{1/3} \ cdot 7.46408092658 ...}}}$

Dette er også gitt, asymptotisk, av integralen

${\ displaystyle {\ frac {1} {2 \ pi}} \ int _ {0}^{\ infty} e^{(2n+1) \ venstre (x-{\ tfrac {1} {2}} \ sinh (2x) \ høyre)} dx ~.}$

Faseløsninger

I de faserommet formuleringen av kvantemekanikken, egentilstandene av kvante harmonisk oscillator i flere forskjellige fremstillinger av quasiprobability fordeling kan bli skrevet i lukket form. Den mest brukte av disse er for Wigner quasiprobability -distribusjon .

Wigner quasiprobability -fordelingen for energien egenstat | n ⟩ er, i de naturlige enheter som er beskrevet ovenfor,

${\ displaystyle F_ {n} (x, p) = {\ frac {(-1)^{n}} {\ pi \ hbar}} L_ {n} \ venstre (2 (x^{2}+p^ {2}) \ høyre) e^{-(x^{2}+p^{2})} ~,}$

hvor L _n er Laguerre -polynomene . Dette eksemplet illustrerer hvordan Hermite- og Laguerre -polynomene er koblet gjennom Wigner -kartet .

I mellomtiden har Husimi Q -funksjonen til de harmoniske oscillator -egenstatene en enda enklere form. Hvis vi jobber i de naturlige enhetene beskrevet ovenfor, har vi det

${\ displaystyle Q_ {n} (x, p) = {\ frac {(x^{2}+p^{2})^{n}} {n!}} {\ frac {e^{-(x ^{2}+p^{2})}} {\ pi}}}$

Denne påstanden kan verifiseres ved hjelp av Segal - Bargmann -transformasjonen . Spesielt siden hevingsoperatoren i Segal - Bargmann -representasjonen ganske enkelt er ganget med og grunntilstanden er den konstante funksjonen 1, er de normaliserte harmoniske oscillatortilstandene i denne representasjonen ganske enkelt . På dette tidspunktet kan vi appellere til formelen for Husimi Q -funksjonen når det gjelder Segal - Bargmann -transformasjonen. ${\ displaystyle z = x+ip}$${\ displaystyle z^{n}/{\ sqrt {n!}}}$

N -dimensjonal isotrop harmonisk oscillator

Den endimensjonale harmonisk oscillator er lett generaliseres til N dimensjoner, hvor N  = 1, 2, 3, ... . I en dimensjon ble posisjonen til partikkelen spesifisert av en enkelt koordinat , x . I N dimensjoner, blir denne erstattet av N posisjonskoordinater, hvilke merker vi x ₁ , ..., x _N . Tilsvarende hver posisjonskoordinat er et momentum; vi merke disse p _en , ...,  p _N . Det kanoniske kommutasjonsforholdet mellom disse operatørene er

${\ displaystyle {\ begin {align} {[} x_ {i}, p_ {j} {]} & = i \ hbar \ delta _ {i, j} \\ {[} x_ {i}, x_ {j } {]} & = 0 \\ {[} p_ {i}, p_ {j} {]} & = 0 \ end {align}}}$

Hamiltonian for dette systemet er

${\ displaystyle H = \ sum _ {i = 1}^{N} \ venstre ({p_ {i}^{2} \ over 2m}+{1 \ over 2} m \ omega^{2} x_ {i }^{2} \ høyre).}$

Som formen på denne Hamiltonian gjør det klart, er den N -dimensjonale harmoniske oscillatoren nøyaktig analog med N uavhengige endimensjonale harmoniske oscillatorer med samme masse og fjærkonstant. I dette tilfellet vil mengdene x ₁ , ..., x _N referere til posisjonene til hver av N -partiklene. Dette er en praktisk egenskap med r ² -potensialet, som gjør at potensiell energi kan skilles i termer avhengig av en koordinat hver.

Denne observasjonen gjør løsningen grei. For et bestemt sett med kvantetall uttrykkes energiens egenfunksjoner for N -dimensjonale oscillatoren i form av de 1 -dimensjonale egenfunksjonene som: ${\ displaystyle \ {n \} \ equiv \ {n_ {1}, n_ {2}, \ dots, n_ {N} \}}$

${\ displaystyle \ langle \ mathbf {x} | \ psi _ {\ {n \}} \ rangle = \ prod _ {i = 1}^{N} \ langle x_ {i} \ mid \ psi _ {n_ { i}} \ rangle}$

I stigeoperatormetoden definerer vi N sett med stigeoperatører,

${\ displaystyle {\ begynne {justert} a_ {i} & = {\ sqrt {m \ omega \ over 2 \ hbar}} \ venstre (x_ {i}+{i \ over m \ omega} p_ {i} \ til høyre), \\ a_ {i}^{\ dolk} & = {\ sqrt {m \ omega \ over 2 \ hbar}} \ venstre (x_ {i}-{i \ over m \ omega} p_ {i} \ høyre). \ ende {justert}}}$

Ved en analog prosedyre til det endimensjonale tilfellet kan vi da vise at hver av a _i og a ^† _i operatørene senker og øker energien med ℏω henholdsvis. Hamiltonian er

${\ displaystyle H = \ hbar \ omega \, \ sum _ {i = 1}^{N} \ venstre (a_ {i}^{\ dolk} \, a_ {i}+{\ frac {1} {2 }}\Ikke sant).}$

Denne Hamiltonian er invariant under den dynamiske symmetri -gruppen U ( N ) (enhetsgruppen i N -dimensjoner), definert av

${\ displaystyle U \, a_ {i}^{\ dolk} \, U^{\ dolk} = \ sum _ {j = 1}^{N} a_ {j}^{\ dolk} \, U_ {ji } \ quad {\ text {for all}} \ quad U \ i U (N),}$

hvor er et element i den definerende matrisepresentasjonen av U ( N ) . ${\ displaystyle U_ {ji}}$

Energinivåene i systemet er

${\ displaystyle E = \ hbar \ omega \ left [(n_ {1}+\ cdots+n_ {N})+{N \ over 2} \ right].}$

${\ displaystyle n_ {i} = 0,1,2, \ dots \ quad ({\ text {energinivået i dimensjon}} i).}$

Som i det endimensjonale tilfellet er energien kvantisert. Jordtilstandsenergien er N ganger den endimensjonale bakkenergien, slik vi forventer å bruke analogien til N uavhengige endimensjonale oscillatorer. Det er en ytterligere forskjell: i det endimensjonale tilfellet tilsvarer hvert energinivå en unik kvantetilstand. I N -dimensjoner, bortsett fra grunntilstanden, er energinivåene degenerert , noe som betyr at det er flere tilstander med samme energi.

Degenerasjonen kan beregnes relativt enkelt. Som et eksempel kan du vurdere det tredimensjonale tilfellet: Definer n  =  n ₁  +  n ₂  +  n ₃ . Alle stater med samme n vil ha samme energi. For et gitt n velger vi en bestemt n ₁ . Deretter n ₂  +  n ₃  =  n  -  n ₁ . Det er n  -  n ₁  + 1 mulige par { n ₂ ,  n ₃ }. n ₂ kan ta på seg verdiene 0 til n  -  n ₁ , og for hver n ₂ er verdien av n ₃ fast. Graden av degenerasjon er derfor:

${\ displaystyle g_ {n} = \ sum _ {n_ {1} = 0}^{n} n-n_ {1} +1 = {\ frac {(n+1) (n+2)} {2} }}$

Formel for generell N og n [ g _n som er dimensjonen til den symmetriske, ureduserbare n ^{maktrepresentasjonen} til enhetsgruppen U ( N ) ]:

${\ displaystyle g_ {n} = {\ binom {N+n-1} {n}}}$

Spesialtilfellet N = 3, gitt ovenfor, følger direkte av denne generelle ligningen. Dette er imidlertid bare sant for skillbare partikler, eller én partikkel i N -dimensjoner (ettersom dimensjoner kan skilles). For tilfellet av N bosoner i et ett-dimensjon harmonisk felle, av degenerering skalaer som antall måter å partisjonere et heltall n ved hjelp av heltall mindre enn eller lik N .

${\ displaystyle g_ {n} = p (N _ {-}, n)}$

Dette oppstår på grunn av begrensningen ved å sette N quanta i en tilstandsket hvor og , som er de samme begrensningene som i heltallspartisjon. ${\ displaystyle \ sum _ {k = 0}^{\ infty} kn_ {k} = n}$${\ displaystyle \ sum _ {k = 0}^{\ infty} n_ {k} = N}$

Eksempel: 3D isotrop harmonisk oscillator

Schrödinger 3D sfæriske harmoniske orbitalløsninger i 2D tetthetsplott; den Mathematica kildekoden som brukes for å generere plottene er på toppen

Schrödinger-ligningen for en partikkel i en sfærisk-symmetrisk tredimensjonal harmonisk oscillator kan løses eksplisitt ved separasjon av variabler; se denne artikkelen for denne saken. Denne prosedyren er analog med separasjonen utført i det hydrogenlignende atomproblemet , men med et annet sfærisk symmetrisk potensial

${\ displaystyle V (r) = {1 \ over 2} \ mu \ omega ^{2} r ^{2},}$

der μ er massen til partikkelen. Fordi m vil bli brukt nedenfor for det magnetiske kvantetallet, er masse angitt med μ , i stedet for m , som tidligere i denne artikkelen.

Løsningen lyder

${\ displaystyle \ psi _ {klm} (r, \ theta, \ phi) = N_ {kl} r^{l} e^{-\ nu r^{2}} L_ {k}^{(l+{1 \ over 2})} (2 \ nu r^{2}) Y_ {lm} (\ theta, \ phi)}$

hvor

${\ displaystyle N_ {kl} = {\ sqrt {{\ sqrt {\ frac {2 \ nu ^{3}} {\ pi}}} {\ frac {2 ^{k+2l+3} \; k! \; \ nu ^{l}} {(2k+2l+1) !!}}}}} ~~}$er en normaliseringskonstant; ;${\ displaystyle \ nu \ equiv {\ mu \ omega \ over 2 \ hbar} ~}$

${\ displaystyle {L_ {k}}^{(l+{1 \ over 2})} (2 \ nu r^{2})}$

er generaliserte Laguerre -polynomer ; Rekkefølgen k på polynomet er et ikke-negativt heltall;

${\ displaystyle Y_ {lm} (\ theta, \ phi) \,}$er en sfærisk harmonisk funksjon ;

ħ er den reduserte Planck -konstanten :   ${\ displaystyle \ hbar \ equiv {\ frac {h} {2 \ pi}} ~.}$

Energiens egenverdi er

${\ displaystyle E = \ hbar \ omega \ left (2k+l+{\ frac {3} {2}} \ right) ~.}$

Energien beskrives vanligvis med det eneste kvantetallet

${\ displaystyle n \ equiv 2k+l ~.}$

Fordi k er et ikke-negativt heltall, for hver til og med n vi har ℓ = 0, 2, ..., n - 2, n og for enhver odde n vi har ℓ = 1, 3, ..., n  - 2 , n . Det magnetiske kvantetallet m er et heltall som tilfredsstiller −ℓ ≤ m ≤ ℓ , så for hver n og ℓ er det 2 ℓ  + 1 forskjellige kvantetilstander , merket med m . Således degenerasjonen på nivå n er

${\ displaystyle \ sum _ {l = \ ldots, n-2, n} (2l+1) = {(n+1) (n+2) \ over 2} ~,}$

hvor summen starter fra 0 eller 1, avhengig av om n er partall eller oddetall. Dette resultatet er i samsvar med dimensjonsformelen ovenfor, og utgjør dimensionaliteten til en symmetrisk representasjon av SU (3) , den relevante degenerasjonsgruppen.

applikasjoner

Harmoniske oscillatorer gitter: fononer

Vi kan utvide forestillingen om en harmonisk oscillator til et endimensjonalt gitter av mange partikler. Tenk på en endimensjonal kvantemekanisk harmonisk kjede av N identiske atomer. Dette er den enkleste kvantemekaniske modellen av et gitter, og vi skal se hvordan fononer oppstår fra det. Formalismen som vi vil utvikle for denne modellen er lett generaliserbar til to og tre dimensjoner.

Som i forrige avsnitt, betegner vi posisjonene til massene med x ₁ , x ₂ , ... , målt fra deres likevektsposisjoner (dvs. x _i = 0 hvis partikkelen i er i likevektsposisjon). I to eller flere dimensjoner er x _i vektormengder. The Hamilton for dette systemet er

${\ displaystyle \ mathbf {H} = \ sum _ {i = 1}^{N} {p_ {i}^{2} \ over 2m}+{1 \ over 2} m \ omega^{2} \ sum _ {\ {ij \} (nn)} (x_ {i} -x_ {j})^{2} ~,}$

hvor m er den (antatte ensartede) massen til hvert atom, og x _i og p _i er posisjons- og momentumoperatørene for det i atomet og summen blir laget over de nærmeste naboene (nn). Imidlertid er det vanlig å omskrive Hamiltonian når det gjelder de normale modusene for bølvektoren i stedet for når det gjelder partikkelkoordinater, slik at man kan arbeide i det mer praktiske Fourier -rommet .

Vi introduserer da et sett med N "normale koordinater" Q _k , definert som de diskrete Fouriertransformasjonene til x s, og N "konjugerte momenta" Π definert som Fouriertransformasjonene til p s,

${\ displaystyle Q_ {k} = {1 \ over {\ sqrt {N}}} \ sum _ {l} e^{ikal} x_ {l}}$

${\ displaystyle \ Pi _ {k} = {1 \ over {\ sqrt {N}}} \ sum _ {l} e^{-ikal} p_ {l} ~.}$

Mengden k _n viser seg å være bølgetallet til fononet, dvs. 2 π dividert med bølgelengden . Det tar på seg kvantiserte verdier, fordi antallet atomer er begrenset.

Dette bevarer de ønskede kommuteringsrelasjonene i enten reelt rom eller bølgevektorrom

${\ displaystyle {\ begynne {justert} \ venstre [x_ {l}, p_ {m} \ høyre] & = i \ hbar \ delta _ {l, m} \\\ venstre [Q_ {k}, \ Pi _ {k '} \ right] & = {1 \ over N} \ sum _ {l, m} e^{ikal} e^{-ik'am} [x_ {l}, p_ {m}] \\ & = {i \ hbar \ over N} \ sum _ {m} e^{iam (k-k ')} = i \ hbar \ delta _ {k, k'} \\\ venstre [Q_ {k}, Q_ {k '} \ høyre] & = \ venstre [\ Pi _ {k}, \ Pi _ {k'} \ høyre] = 0 ~. \ ende {justert}}}$

Fra det generelle resultatet

${\ displaystyle {\ begynne {justert} \ sum _ {l} x_ {l} x_ {l+m} & = {1 \ over N} \ sum _ {kk '} Q_ {k} Q_ {k'} \ sum _ {l} e^{ial \ left (k+k '\ right)} e^{iamk'} = \ sum _ {k} Q_ {k} Q _ {-k} e^{iamk} \\\ sum _ {l} {p_ {l}}^{2} & = \ sum _ {k} \ Pi _ {k} \ Pi _ {-k} ~, \ ende {justert}}}$

det er lett å vise, gjennom elementær trigonometri, at det potensielle energitermet er

${\ displaystyle {1 \ over 2} m \ omega ^{2} \ sum _ {j} (x_ {j} -x_ {j+1}) ^{2} = {1 \ over 2} m \ omega ^ {2} \ sum _ {k} Q_ {k} Q _ {-k} (2-e^{ika} -e^{-ika}) = {1 \ over 2} m \ sum _ {k} {\ omega _ {k}}^{2} Q_ {k} Q _ {-k} ~,}$

hvor

${\ displaystyle \ omega _ {k} = {\ sqrt {2 \ omega ^{2} (1- \ cos (ka))}}} ~.}$

Hamiltonian kan skrives i bølgevektorrom som

${\ displaystyle \ mathbf {H} = {1 \ over {2m}} \ sum _ {k} \ left ({\ Pi _ {k} \ Pi _ {-k}}+m^{2} \ omega _ {k}^{2} Q_ {k} Q _ {-k} \ høyre) ~.}$

Vær oppmerksom på at koblingene mellom posisjonsvariablene er transformert bort; hvis Qs og weres var hermitiske (som de ikke er), ville den transformerte Hamiltonian beskrive N ukoblede harmoniske oscillatorer.

Kvantiseringsformen avhenger av valg av grensebetingelser; For enkelhets skyld pålegger vi periodiske grensebetingelser som definerer ( N + 1) atomet som ekvivalent med det første atomet. Fysisk tilsvarer dette å bli med i kjeden i enden. Den resulterende kvantiseringen er

${\ displaystyle k = k_ {n} = {2n \ pi \ over Na} \ quad {\ hbox {for}} \ n = 0, \ pm 1, \ pm 2, \ ldots, \ pm {N \ over 2 }. \}$

Den øvre grensen til n kommer fra minimum bølgelengde, som er to ganger gitteravstanden a , som diskutert ovenfor.

De harmoniske oscillatorens egenverdier eller energinivåer for modus ω _k er

${\ displaystyle E_ {n} = \ venstre ({1 \ over 2}+n \ høyre) \ hbar \ omega _ {k} \ quad {\ hbox {for}} \ quad n = 0,1,2,3 , \ ldots}$

Hvis vi ignorerer nullpunktsenergien, er nivåene jevnt fordelt på

${\ displaystyle \ hbar \ omega, \, 2 \ hbar \ omega, \, 3 \ hbar \ omega, \, \ ldots}$

Så en eksakt mengde energi ħω må tilføres det harmoniske oscillatorgitteret for å skyve den til neste energinivå. I analogi med fotonettet når det elektromagnetiske feltet er kvantisert, kalles kvanten for vibrasjonsenergi et fonon .

Alle kvantesystemer viser bølgelignende og partikkellignende egenskaper. De partikkellignende egenskapene til fononet forstås best ved å bruke metodene for andre kvantisering og operatørteknikker beskrevet senere.

I kontinuumgrensen, a → 0, N → ∞, mens Na holdes fast. Kanonisk koordinatene Q _k tilfalle utkoblet fart moduser av et skalarfelt, , mens den posisjonsindeksen i ( ikke forskyvningen dynamiske variable ) blir parameteren x argumentet av skalarfeltet, .${\ displaystyle \ phi _ {k}}$${\ displaystyle \ phi (x, t)}$

Molekylære vibrasjoner

• Vibrasjonene til et diatomisk molekyl er et eksempel på en to-kroppsversjon av den kvanteharmoniske oscillatoren. I dette tilfellet er vinkelfrekvensen gitt av

${\ displaystyle \ omega = {\ sqrt {\ frac {k} {\ mu}}}}$

hvor er den reduserte massen og og er massene til de to atomene.${\ displaystyle \ mu = {\ frac {m_ {1} m_ {2}} {m_ {1}+m_ {2}}}}$${\ displaystyle m_ {1}}$${\ displaystyle m_ {2}}$

• Den Hookes-atomet er en enkel modell av den helium -atomet ved hjelp av kvante harmonisk oscillator.
• Modellering av fononer, som diskutert ovenfor.
• En ladning med masse i et jevnt magnetfelt er et eksempel på en endimensjonal kvanteharmonisk oscillator: Landau-kvantisering .${\ displaystyle q}$${\ displaystyle m}$${\ displaystyle \ mathbf {B}}$

Se også

Referanser

Eksterne linker

• Quantum Harmonic Oscillator
• Begrunnelse for valg av stigeoperatører
• Levende 3D -intensitetsplott av kvanteharmonisk oscillator
• Drevet og dempet kvanteharmonisk oscillator (forelesningsnotater selvfølgelig "kvanteoptikk i elektriske kretser")