Partieres stier i Schwarzschild -løsningen til Einsteins feltligninger
I generell relativitets , Schwarz geodesics beskrive bevegelsen av prøvepartikler i gravitasjonsfelt av en sentral faste masse dvs. bevegelse i den Schwarz metrisk. Schwarzschild geodesics har vært sentrale i valideringen av Einsteins teori om generell relativitet . For eksempel gir de nøyaktige spådommer om den uregelmessige presesjonen til planetene i solsystemet og om nedbøyning av lys ved tyngdekraften.

Schwarzschild geodesics gjelder bare bevegelsen av massepartikler så små at de bidrar lite til gravitasjonsfeltet. Imidlertid er de svært nøyaktige i mange astrofysiske scenarier, forutsatt at de er mange ganger mindre enn sentralmassen , f.eks. For planeter som kretser rundt solen. Schwarzschild geodesics er også en god tilnærming til den relative bevegelsen til to legemer med vilkårlig masse, forutsatt at Schwarzschild -massen er satt lik summen av de to individuelle massene og . Dette er viktig for å forutsi bevegelsen til binære stjerner i generell relativitet.





Historisk sammenheng
Schwarzschild -metrikken er navngitt til ære for oppdageren Karl Schwarzschild , som fant løsningen i 1915, bare omtrent en måned etter publiseringen av Einsteins teori om generell relativitet. Det var den første eksakte løsningen av Einstein -feltligningene enn den trivielle flatromsløsningen .
I 1931 publiserte Yusuke Hagihara et papir som viser at banen til en testpartikkel i Schwarzschild -metrikken kan uttrykkes i form av elliptiske funksjoner .
Schwarzschild metrisk
En eksakt løsning på Einstein-feltligningene er Schwarzschild-metriket , som tilsvarer det ytre gravitasjonsfeltet til et uladet, ikke-roterende, sfærisk symmetrisk masselegeme . Schwarzschild -løsningen kan skrives som


hvor
-
 er riktig tid (tiden målt med en klokke som beveger seg med partikkelen) i sekunder,
er riktig tid (tiden målt med en klokke som beveger seg med partikkelen) i sekunder,
-
 er lysets hastighet i meter per sekund,
er lysets hastighet i meter per sekund,
-
 er tidskoordinaten (tiden målt med en stasjonær klokke ved uendelig) i sekunder,
er tidskoordinaten (tiden målt med en stasjonær klokke ved uendelig) i sekunder,
-
 er radialkoordinaten (omkretsen av en sirkel sentrert i stjernen dividert med ) i meter,
er radialkoordinaten (omkretsen av en sirkel sentrert i stjernen dividert med ) i meter,
-
 er kolatituden (vinkel fra nord) i radianer,
er kolatituden (vinkel fra nord) i radianer,
-
 er lengdegrad i radianer, og
er lengdegrad i radianer, og
-
 er Schwarzschild -radiusen til den massive kroppen (i meter), som er relatert til dens masse av
er Schwarzschild -radiusen til den massive kroppen (i meter), som er relatert til dens masse av


- hvor er gravitasjonskonstanten . Den klassiske Newton -teorien om tyngdekraften gjenopprettes i grensen når forholdet går til null. I denne grensen går metriken tilbake til den som er definert av spesiell relativitet .


I praksis er dette forholdet nesten alltid ekstremt lite. For eksempel, Schwarz radius er av jorden omtrent 9 mm ( 3- / 8 tomme); på overflaten av jorden er korreksjonene til Newtons gravitasjon bare en del av en milliard. Schwarzschild -radiusen til solen er mye større, omtrent 2953 meter, men på overflaten er forholdet omtrent 4 deler i en million. En hvit dvergstjerne er mye tettere, men selv her er forholdet på overflaten omtrent 250 deler i en million. Forholdet blir bare stort nær ultratette objekter som nøytronstjerner (hvor forholdet er omtrent 50%) og sorte hull .


Baner av testpartikler

Sammenligning mellom bane til en testpartikkel i Newtonian (venstre) og Schwarzschild (høyre) romtid; Legg merke til
apsidalpresesjonen til høyre.
Vi kan forenkle problemet ved å bruke symmetri for å eliminere en variabel fra vurdering. Siden Schwarzschild -metrikken er symmetrisk om , vil enhver geodesikk som begynner å bevege seg i det flyet forbli i det planet på ubestemt tid (planet er totalt geodetisk ). Derfor orienterer vi koordinatsystemet slik at partikkelens bane ligger i det planet, og fikser koordinaten slik at metrisk (for dette planet) forenkles til




To bevegelseskonstanter (verdier som ikke endres over riktig tid ) kan identifiseres (jf. Avledningen gitt nedenfor ). Den ene er den totale energien :



og den andre er den spesifikke vinkelmomentet :

hvor L er det totale vinkelmomentet til de to legemene, og er den reduserte massen . Når er den reduserte massen omtrent lik . Noen ganger antas det . Når det gjelder planeten Merkur denne forenklingen introduserer en feil som er mer enn dobbelt så stor som den relativistiske effekten. Når man diskuterer geodesikk, kan det betraktes som fiktivt, og det som betyr noe er konstantene og . For å dekke all mulig geodesikk, må vi vurdere tilfeller der det er uendelig (som gir baner for fotoner ) eller imaginær (for takyoniske geodesika). For det fotoniske tilfellet må vi også spesifisere et tall som tilsvarer forholdet mellom de to konstantene, nemlig som kan være null eller et ikke-null reelt tall.









Erstatter disse konstantene i definisjonen av Schwarzschild -metrikken

gir en bevegelsesligning for radius som en funksjon av riktig tid :


Den formelle løsningen på dette er

Vær oppmerksom på at kvadratroten vil være imaginær for takyonisk geodesikk.
Ved å bruke forholdet høyere opp mellom og , kan vi også skrive



Siden asymptotisk integranden er omvendt proporsjonal med , dette viser at i referanseramme hvis nærmer det gjør det eksponentielt uten noen gang å nå det. Men som en funksjon av , kommer frem .







Løsningene ovenfor er gyldige mens integranden er begrenset, men en totalløsning kan innebære to eller uendelige stykker, hver beskrevet av integralen, men med vekslende tegn for kvadratroten.
Når og , kan vi løse for og eksplisitt:





og for fotonisk geodesikk ( ) med null vinkelmoment


(Selv om riktig tid er trivielt i det fotoniske tilfellet, kan man definere en affin parameter , og så er løsningen på den geodesiske ligningen .)


Et annet løsbart tilfelle er det der og og er konstant. I volumet der dette gir den riktige tiden





Dette er nær løsninger med små og positive. Utenfor den løsningen er tachyonic og "riktig tid" er plass-like:




Dette er i nærheten av andre takyoniske løsninger med små og negative. Den konstante takyoniske geodesikken utenfor blir ikke videreført av en konstant geodesikk inni , men fortsetter heller inn i et "parallelt ytre område" (se Kruskal - Szekeres koordinater ). Andre takyoniske løsninger kan komme inn i et svart hull og gå ut igjen i det parallelle ytre området. Den konstante t -løsningen inne i hendelseshorisonten ( ) fortsetter med en konstant t -løsning i et hvitt hull .






Når vinkelmomentet ikke er null, kan vi erstatte avhengigheten av riktig tid med en avhengighet av vinkelen ved å bruke definisjonen av


som gir ligningen for bane

hvor, for korthet, to lengdeskalaer og , har blitt definert av



Vær oppmerksom på at i det takyoniske tilfellet vil det være imaginært og ekte eller uendelig.


Den samme ligningen kan også utledes ved hjelp av en Lagrangian -tilnærming eller Hamilton - Jacobi -ligningen (se nedenfor ). Løsningen på bane -ligningen er

Dette kan uttrykkes i form av Weierstrass elliptiske funksjon .

Lokale og forsinkede hastigheter
I motsetning til i klassisk mekanikk, i Schwarzschild koordinater og er ikke de radiale og tverrgående komponentene i den lokale hastigheten (i forhold til en stasjonær observatør), i stedet gir de komponentene for celeriteten som er relatert til av







for radial og

for den tverrgående bevegelseskomponenten, med . Koordinatbokføreren langt borte fra scenen observerer den shapiro-forsinkede hastigheten , som er gitt av forholdet


-
 og .
og .
Tidsutvidelsesfaktoren mellom bokføreren og den bevegelige testpartikkelen kan også settes inn i skjemaet

der telleren er gravitasjon, og nevneren er den kinematiske komponenten i tidsutvidelsen. For en partikkel som faller inn fra uendelig er venstre faktor lik den høyre faktoren, siden den fallende hastigheten samsvarer med rømningshastigheten i dette tilfellet.


De to konstantene vinkelmoment og total energi til en testpartikkel med masse er i form av




og

hvor

og

For massive testpartikler er Lorentz -faktoren og er riktig tid, mens for masseløse partikler som fotoner er satt til og tar rollen som en affin parameter. Hvis partikkelen er masseløs , erstattes den med og med , hvor er Planck -konstanten og den lokalt observerte frekvensen.












Eksakt løsning ved hjelp av elliptiske funksjoner
Den grunnleggende ligningen for bane er lettere å løse hvis den uttrykkes i form av invers radius 

Høyre side av denne ligningen er et kubisk polynom , som har tre røtter , angitt her som u 1 , u 2 og u 3

Summen av de tre røttene er lik koeffisienten for u 2 -termen

Et kubisk polynom med reelle koeffisienter kan enten ha tre virkelige røtter, eller en ekte rot og to komplekse konjugerte røtter. Hvis alle tre røttene er reelle tall , er røttene merket slik at u 1 < u 2 < u 3 . Hvis det i stedet bare er en ekte rot, så er det betegnet som u 3 ; de komplekse konjugerte røttene er merket u 1 og u 2 . Ved å bruke Descartes tegnregel kan det være høyst én negativ rot; u 1 er negativ hvis og bare hvis b < a . Som diskutert nedenfor er røttene nyttige for å bestemme typer mulige baner.
Gitt denne merkingen av røttene, er løsningen på den grunnleggende orbitallikningen

hvor sn representerer sinus amplitudinus -funksjonen (en av Jacobi elliptiske funksjoner ) og δ er en integrasjonskonstant som gjenspeiler utgangsposisjonen. Den elliptiske modulen k for denne elliptiske funksjonen er gitt av formelen

Newtonsk grense
For å gjenopprette den newtonske løsningen for planetbanene, tar man grensen når Schwarzschild -radius r s går til null. I dette tilfellet blir den tredje roten u 3 grovt og mye større enn u 1 eller u 2 . Derfor har modulen k en tendens til null; i den grensen blir sn den trigonometriske sinusfunksjonen

I samsvar med Newtons løsninger for planetariske bevegelser beskriver denne formelen en fokal konisk eksentrisitet e

Hvis u 1 er et positivt reelt tall, så er bane en ellipse hvor u 1 og u 2 representerer avstandene til henholdsvis den lengste og nærmeste tilnærmingen. Hvis u 1 er null eller et negativt reelt tall, er bane henholdsvis en parabel eller en hyperbola . I disse to sistnevnte tilfellene representerer u 2 avstanden til nærmeste tilnærming; siden banen går til uendelig ( u = 0), er det ingen avstand til den lengste tilnærmingen.
Røtter og oversikt over mulige baner
En rot representerer et punkt i bane der derivatet forsvinner, dvs. hvor . Ved et slikt vendepunkt når u et maksimum, et minimum eller et bøyningspunkt, avhengig av verdien til det andre derivatet, som er gitt av formelen

![{\ displaystyle {\ frac {d ^{2} u} {d \ varphi ^{2}}} = {\ frac {r _ {\ rm {s}}} {2}} \ venstre [\ venstre (u- u_ {2} \ høyre) \ venstre (u-u_ {3} \ høyre)+\ venstre (u-u_ {1} \ høyre) \ venstre (u-u_ {3} \ høyre)+\ venstre (u- u_ {1} \ høyre) \ venstre (u-u_ {2} \ høyre) \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbff935c41511467f9e16003f2e913b861a3216b)
Hvis alle tre røttene er forskjellige reelle tall, er det andre derivatet henholdsvis positivt, negativt og positivt ved u 1 , u 2 og u 3 . Det følger at en graf med u mot φ enten kan svinge mellom u 1 og u 2 , eller den kan bevege seg bort fra u 3 mot uendelig (som tilsvarer at r går til null). Hvis u 1 er negativ, vil bare en del av en "oscillasjon" faktisk forekomme. Dette tilsvarer at partikkelen kommer fra uendelig, nærmer seg sentralmassen og deretter beveger seg bort igjen mot uendelig, som den hyperbolske banen i den klassiske løsningen.
Hvis partikkelen har akkurat den rette energimengden for vinkelmomentet, vil u 2 og u 3 smelte sammen. Det er tre løsninger i denne saken. Banen kan spire inn til , nærme seg denne radius som (asymptotisk) en synkende eksponensial i φ, τ eller t . Eller man kan ha en sirkulær bane i den radiusen. Eller man kan ha en bane som spiraler ned fra den radius til det sentrale punktet. Den aktuelle radius kalles den indre radius og er mellom og 3 ganger r s . En sirkulær bane oppstår også når u 2 er lik u 1 , og dette kalles den ytre radius. Disse forskjellige typer baner diskuteres nedenfor.


Hvis partikkelen kommer til sentralmassen med tilstrekkelig energi og tilstrekkelig lav vinkelmoment, vil bare u 1 være ekte. Dette tilsvarer at partikkelen faller ned i et svart hull. Bane spiraler inn med en endelig endring i φ.
Presisjon av baner
Funksjonen sn og dens kvadrat sn 2 har perioder på henholdsvis 4 K og 2 K , hvor K er definert av ligningen

Derfor er endringen i φ over en oscillasjon av u (eller, ekvivalent, en oscillasjon av r ) lik

I den klassiske grensen nærmer u 3 seg og er mye større enn u 1 eller u 2 . Derfor er k 2 omtrentlig


Av de samme grunnene er nevneren til Δφ omtrent

Siden modulen k er nær null, kan perioden K utvides i potens på k ; til laveste rekkefølge, gir denne utvidelsen

Ved å erstatte disse tilnærmingene til formelen for Δφ gir du en formel for vinkelforskridelse per radiell oscillasjon

For en elliptisk bane representerer u 1 og u 2 inversene til henholdsvis de lengste og korteste avstandene. Disse kan uttrykkes i form av ellipsens halvstore akse A og dens baneeksentrisitet e ,

å gi

Ved å erstatte definisjonen av r s får den siste ligningen

Bøyning av lys etter tyngdekraften
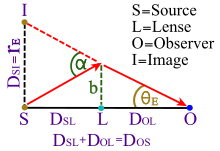
Diagram over gravitasjonslinser av en kompakt kropp
I grensen når partikkelmassen m går til null (eller, tilsvarende hvis lyset er på vei direkte mot sentralmassen, ettersom lengdeskalaen a går til uendelig), blir ligningen for bane

Ved å ekspandere i potens for , gir den ledende ordrebetegnelsen i denne formelen den omtrentlige vinkelbøyningen δ φ for en masseløs partikkel som kommer inn fra uendelig og går tilbake til uendelig:


Her, b er den innvirkning parameteren , noe større enn avstanden til nærmeste tilnærming , r 3 :

Selv om denne formelen er omtrentlig, er den nøyaktig for de fleste målinger av gravitasjonslinser på grunn av forholdets litenhet . For lett beite på overflaten av solen, er den omtrentlige vinkelbøyningen omtrent 1,75 buesekunder , omtrent en milliondel av en sirkel.

Når lysbølgepakken (eller dens kvante, foton) beveger seg på den avbøyde banen som forutsies ved lysbøyning, samhandler bølgefunksjonen fortsatt med den buede rom-tid-geometrien rundt geodetikken og blir forvrengt. Det rapporteres at forvrengningen er signifikant for nivået som kan måles.
Forholdet til Newtonsk fysikk
Effektiv radial potensiell energi
Bevegelsesligningen for partikkelen avledet ovenfor

kan skrives om ved hjelp av definisjonen av Schwarzschild radius r s as
![{\ displaystyle {\ frac {1} {2}} m \ left ({\ frac {dr} {d \ tau}} \ right)^{2} = \ left [{\ frac {E^{2}} {2mc^{2}}}-{\ frac {1} {2}} mc^{2} \ right]+{\ frac {GMm} {r}}-{\ frac {L^{2}} { 2 \ mu r^{2}}}+{\ frac {G (M+m) L^{2}} {c^{2} \ mu r^{3}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78fa7da802311c62479b99d4078fbaef08a0dbf0)
som tilsvarer en partikkel som beveger seg i et endimensjonalt effektivt potensial

De to første begrepene er velkjente klassiske energier, det første er den attraktive Newtonsk gravitasjonspotensialenergi og det andre tilsvarer den frastøtende "sentrifugale" potensielle energien ; Imidlertid er det tredje uttrykket en attraktiv energi som er unik for generell relativitet . Som vist nedenfor og andre steder får denne invers-kubiske energien elliptiske baner til å gå gradvis ut med en vinkel δφ per omdreining

hvor A er halv-hovedaksen og e er eksentrisiteten.
Det tredje uttrykket er attraktivt og dominerer ved små r -verdier, noe som gir en kritisk indre radius r indre der en partikkel trekkes ubønnhørlig innover til r = 0; denne indre radius er en funksjon av partikkels vinkelmoment per masseenhet eller, tilsvarende, en lengdeskala definert ovenfor.
Sirkulære baner og deres stabilitet
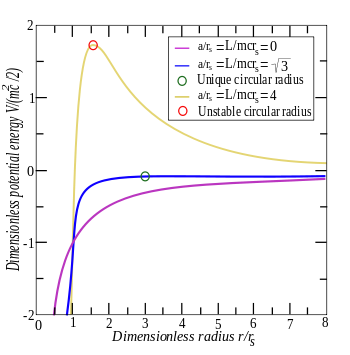
Effektivt radialt potensial for forskjellige vinkelmoment. Ved små radier faller energien nedfallende, noe som får partikkelen til å trekkes ubønnhørlig innover til
r = 0. Men når det normaliserte vinkelmomentet er lik kvadratroten til tre, er en metastabil sirkulær bane mulig ved radius markert med en grønn sirkel . Ved høyere vinkelmoment er det en betydelig sentrifugalbarriere (oransje kurve) og en ustabil indre radius, markert med rødt.

Det effektive potensialet V kan skrives om når det gjelder lengden .

![{\ displaystyle V (r) = {\ frac {\ mu c^{2}} {2}} \ venstre [-{\ frac {r _ {\ rm {s}}} {r}}+{\ frac { a^{2}} {r^{2}}}-{\ frac {r _ {\ rm {s}} a^{2}} {r^{3}}} \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/532ca22c56a1612492c5e868274d9257f0eba729)
Sirkulære baner er mulige når den effektive kraften er null
![{\ displaystyle F =-{\ frac {dV} {dr}} =-{\ frac {\ mu c^{2}} {2r^{4}}} \ venstre [r _ {\ rm {s}} r ^{2} -2a^{2} r+3r _ {\ rm {s}} a^{2} \ right] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417d63a6c334cbf801d43b95f97d09f8b58ebd7b)
dvs. når de to attraktive kreftene - Newtonsk tyngdekraft (første ledd) og tiltrekningen som er unik for generell relativitet (tredje begrep) - er nøyaktig balansert av den frastøtende sentrifugalkraften (andre leddet). Det er to radier der denne balanseringen kan oppstå, betegnet her som r indre og r ytre
![{\ displaystyle {\ begynne {justert} r _ {\ tekst {ytre}} & = {\ frac {a^{2}} {r _ {\ rm {s}}}} \ venstre (1+{\ sqrt {1 -{\ frac {3r _ {\ rm {s}}^{2}} {a^{2}}}}} \ høyre) \\ [3pt] r _ {\ text {inner}} & = {\ frac { a^{2}} {r _ {\ rm {s}}}} \ venstre (1-{\ sqrt {1-{\ frac {3r _ {\ rm {s}}^{2}} {a^{2 }}}}}} \ right) = {\ frac {3a^{2}} {r _ {\ text {ytre}}}} \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52992e7a17eae29b6c05d60f99a6bd2d9af795bc)
som oppnås ved bruk av den kvadratiske formelen . Den indre radius r indre er ustabil, fordi den attraktive tredje kraften styrkes mye raskere enn de to andre kreftene når r blir liten; hvis partikkelen glir litt innover fra r indre (hvor alle tre kreftene er i balanse), dominerer den tredje kraften de to andre og trekker partikkelen ubønnhørlig innover til r = 0. Ved den ytre radius er imidlertid de sirkulære banene stabile; det tredje uttrykket er mindre viktig, og systemet oppfører seg mer som det ikke-relativistiske Kepler-problemet .
Når a er mye større enn r s (det klassiske tilfellet), blir disse formlene omtrent
![{\ displaystyle {\ begynne {justert} r _ {\ tekst {ytre}} og \ ca {\ frac {2a^{2}} {r _ {\ rm {s}}}} \\ [3pt] r _ {\ tekst {indre}} og \ ca {\ frac {3} {2}} r _ {\ rm {s}} \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df56aeae454867cb6038bbf8a624a9b34d171a92)
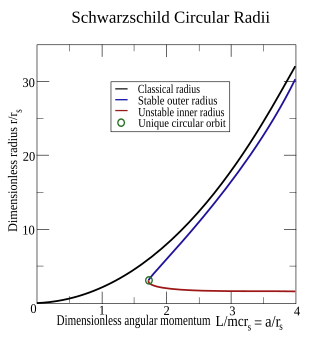
De stabile og ustabile radiene er plottet mot det normaliserte vinkelmomentet i henholdsvis blått og rødt. Disse kurvene møtes i en unik sirkulær bane (grønn sirkel) når det normaliserte vinkelmomentet er lik kvadratroten til tre. Til sammenligning er den klassiske radius forutsagt fra
sentripetalakselerasjonen og Newtons tyngdelov tegnet i svart.
Substituere definisjonene av en og r r i r ytre utbytter den klassiske formel for en partikkel av massen m i bane rundt et legeme av masse M .

der ω φ er partikkelens orbitale vinkelhastighet. Denne formelen oppnås i ikke-relativistisk mekanikk ved å sette sentrifugalkraften lik den newtonske gravitasjonskraften:

Hvor er den reduserte massen .

I vår notasjon er den klassiske orbitale vinkelhastigheten lik

På den andre enden, når en 2 nærmer seg 3 r s 2 ovenfra, konvergerer de to radiene til en enkelt verdi

De kvadratiske løsningene ovenfor sikrer at r ytre alltid er større enn 3 r s , mens r indre ligger mellom 3 ⁄ 2 r s og 3 r s . Sirkulære baner som er mindre enn 3 / 2 r s er ikke mulig. For masseløse partikler, en går mot uendelig, noe som tyder på at det er en sirkulær bane for fotoner i r inner = 3- / 2- r s . Sfæren i denne radius er noen ganger kjent som foton -sfæren .
Presesjon av elliptiske baner

I det ikke-relativistiske
Kepler-problemet følger en partikkel den samme perfekte
ellipsen (rød bane) for alltid.
Generell relativitet introduserer en tredje kraft som tiltrekker partikkelen litt sterkere enn Newtonsk tyngdekraft, spesielt ved små radier. Denne tredje kraft fører til at partikkelens elliptiske bane for å
presesere (cyan bane) i retningen av dens rotasjon; denne effekten er målt i
Merkur ,
Venus og Jorden. Den gule prikken i banene representerer attraksjonens sentrum, for eksempel
solen .
Omløpspresesjonshastigheten kan oppnås ved hjelp av denne radiale effektiv potensialet V . Et lite radialt avvik fra en sirkulær bane med radius r ytre vil svinge stabilt med en vinkelfrekvens
![\ omega _ {r}^{2} = {\ frac {1} {m}} \ venstre [{\ frac {d^{2} V} {dr^{2}}} \ høyre] _ {r = r _ {\ mathrm {ytre}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894cef5f743b66cd47bfe665608a9fff3e703799)
som er lik

Å ta kvadratroten på begge sider og utføre en utvidelse av
Taylor -serien
![{\ displaystyle \ omega _ {r} = \ omega _ {\ varphi} \ venstre [1-{\ frac {3r _ {\ rm {s}}^{2}} {4a^{2}}}+{\ matematikk {O}} \ venstre ({\ frac {r _ {\ rm {s}}^{4}} {a^{4}}} \ høyre) \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a71fab0af7c17cf18e5c949ccb3bb3c3bedfc6c4)
Multiplisering med perioden T for en revolusjon gir forløpet av bane per revolusjon

hvor vi har brukt ω φ T = 2 п og definisjonen av lengdeskalaen a . Erstatter definisjonen av Schwarzschild radius r s gir

Dette kan forenkles ved hjelp av den elliptiske bane semiaxis A og eksentrisitet e relatert til formelen

å gi presesjonen vinkel

Matematiske avledninger av orbitalligningen
Christoffel -symboler
De ikke-forsvinnende Christoffel-symbolene for Schwarzschild-metrikken er:
![{\ displaystyle {\ begynne {justert} \ Gamma _ {rt}^{t} =-\ Gamma _ {rr}^{r} & = {\ frac {r _ {\ rm {s}}} {2r (r -r _ {\ rm {s}})}} \\ [3pt] \ Gamma _ {tt}^{r} & = {\ frac {r _ {\ rm {s}} (r-r _ {\ rm {s }})) {2r^{3}}} \\ [3pt] \ Gamma _ {\ phi \ phi}^{r} & = (r _ {\ rm {s}}-r) \ sin^{2} (\ theta) \\ [3pt] \ Gamma _ {\ theta \ theta}^{r} & = r _ {\ rm {s}}-r \\ [3pt] \ Gamma _ {r \ theta}^{\ theta} = \ Gamma _ {r \ phi}^{\ phi} & = {\ frac {1} {r}} \\ [3pt] \ Gamma _ {\ phi \ phi}^{\ theta} & =- \ sin (\ theta) \ cos (\ theta) \\ [3pt] \ Gamma _ {\ theta \ phi}^{\ phi} & = \ cot (\ theta) \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ebd981ec7f21f8385ffc13af5084c04f17ae29f)
Geodesisk ligning
I følge Einsteins teori om generell relativitet reiser partikler av ubetydelig masse langs geodesikk i romtiden. I flat romtid, langt fra en kilde til tyngdekraften, tilsvarer disse geodesikkene rette linjer; de kan imidlertid avvike fra rette linjer når romtiden er buet. Ligningen for de geodesiske linjene er

der Γ representerer Christoffelsymbolet og variabelen parametrerer partikkelenes vei gjennom romtiden , dens såkalte verdenslinje . Christoffelsymbolet avhenger bare av den metriske tensoren , eller rettere sagt av hvordan den endres med posisjon. Variabelen er et konstant multiplum av riktig tid for tidlignende baner (som beveges av massive partikler), og regnes vanligvis som lik den. For lyslignende (eller null) baner (som beveges av masseløse partikler som fotonet ), er riktig tid null og kan strengt tatt ikke brukes som variabel . Likevel kan lyslignende baner avledes som den ultrarelativistiske grensen for tidslignende baner, det vil si grensen når partikkelmassen m går til null mens den totale energien holdes fast.





Derfor, for å løse bevegelsen av en partikkel, er den mest enkle måten å løse den geodesiske ligningen, en tilnærming vedtatt av Einstein og andre. Schwarzschild -metrikken kan skrives som

hvor de to funksjonene og dens gjensidige er definert for å være korte. Fra denne metrikken kan Christoffelsymbolene beregnes og resultatene erstattes med de geodesiske ligningene



![{\ displaystyle {\ begin {align} 0 & = {\ frac {d^{2} \ theta} {dq^{2}}}+{\ frac {2} {r}} {\ frac {d \ theta} {dq}} {\ frac {dr} {dq}}-\ sin \ theta \ cos \ theta \ venstre ({\ frac {d \ phi} {dq}} \ høyre)^{2} \\ [3pt] 0 & = {\ frac {d^{2} \ phi} {dq^{2}}}+{\ frac {2} {r}} {\ frac {d \ phi} {dq}} {\ frac {dr } {dq}}+2 \ cot \ theta {\ frac {d \ phi} {dq}} {\ frac {d \ theta} {dq}} \\ [3pt] 0 & = {\ frac {d^{2 } t} {dq^{2}}}+{\ frac {1} {w}} {\ frac {dw} {dr}} {\ frac {dt} {dq}} {\ frac {dr} {dq }} \\ [3pt] 0 & = {\ frac {d^{2} r} {dq^{2}}}+{\ frac {1} {2v}} {\ frac {dv} {dr}} \ venstre ({\ frac {dr} {dq}} \ høyre)^{2}-{\ frac {r} {v}} \ venstre ({\ frac {d \ theta} {dq}} \ høyre)^{ 2}-{\ frac {r \ sin^{2} \ theta} {v}} \ venstre ({\ frac {d \ phi} {dq}} \ høyre)^{2}+{\ frac {c^ {2}} {2v}} {\ frac {dw} {dr}} \ venstre ({\ frac {dt} {dq}} \ høyre)^{2} \ end {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7c637c4ac82e06d91b30a2a2a9286d4b52ce5f6)
Det kan verifiseres som en gyldig løsning ved å erstatte den første av disse fire ligningene. Ved symmetri må bane være plan, og vi står fritt til å ordne koordinatrammen slik at ekvatorialplanet er planets bane. Denne løsningen forenkler den andre og fjerde ligningen.


For å løse de andre og tredje ligninger, er det tilstrekkelig å dele dem med og hhv.


![{\ displaystyle {\ begin {align} 0 & = {\ frac {d} {dq}} \ venstre [\ ln {\ frac {d \ phi} {dq}}+\ ln r^{2} \ right] \ \ [3pt] 0 & = {\ frac {d} {dq}} \ venstre [\ ln {\ frac {dt} {dq}}+\ ln w \ høyre], \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd6b6cb65149f9e94e2aaed1743e7adf905c0aa9)
som gir to bevegelseskonstanter.
Lagrangisk tilnærming
Fordi testpartikler følger geodesikk i en fast metrisk, kan partiklernes baner bestemmes ved hjelp av variabelen, også kalt Lagrangian -tilnærmingen. Geodesikk i romtid er definert som kurver som små lokale variasjoner i koordinatene deres (mens de holder endepunktene hendte fast) ikke gjør noen vesentlig endring i deres totale lengde s . Dette kan uttrykkes matematisk ved hjelp av beregningen av variasjoner

hvor τ er riktig tid , er s = cτ buelengden i romtid og T er definert som

i analogi med kinetisk energi . Hvis derivatet med hensyn til riktig tid er representert med en prikk for korthet

T kan skrives som

Konstante faktorer (for eksempel c eller kvadratroten av to) påvirker ikke svaret på variasjonsproblemet; Derfor tar variasjonen inne i integralet Hamilton's prinsipp

Løsningen på variasjonsproblemet er gitt av Lagranges ligninger

Når de brukes på t og φ , avslører disse ligningene to bevegelseskonstanter
![{\ displaystyle {\ begin {align} {\ frac {d} {d \ tau}} \ left [r^{2} {\ frac {d \ varphi} {d \ tau}} \ right] & = 0, \\ {\ frac {d} {d \ tau}} \ venstre [\ venstre (1-{\ frac {r _ {\ rm {s}}} {r}} \ høyre) {\ frac {dt} {d \ tau}} \ høyre] & = 0, \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ec20bcaa6c2888ba4c6bac76901c7e22fa92be)
som kan uttrykkes i form av to konstante lengdeskalaer, og


Som vist ovenfor gir substitusjon av disse ligningene i definisjonen av Schwarzschild -metriket ligningen for bane.
Hamiltonsk tilnærming
En Lagrangian -løsning kan omformes til en tilsvarende Hamiltonian -form. I dette tilfellet er Hamiltonian gitt av


Nok en gang kan bane være begrenset til av symmetri. Siden og ikke vises på Hamiltonian, er deres konjugerte momenta konstante; de kan uttrykkes i form av lysets hastighet og to konstante lengdeskalaer og






Derivatene med hensyn til riktig tid er gitt av

Deling av den første ligningen med den andre gir orbitalligningen

Radialmomentet p r kan uttrykkes i form av r ved bruk av hamiltons konstans ; dette gir den grunnleggende orbitalligningen


Hamilton - Jacobi tilnærming
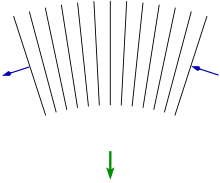
Bøyning av bølger i et gravitasjonsfelt. På grunn av tyngdekraften går tiden langsommere i bunnen enn på toppen, noe som får bølgefrontene (vist i svart) til å bøye seg nedover gradvis. Den grønne pilen viser retningen til den tilsynelatende "gravitasjonsattraksjonen".
Orbitalligningen kan stammer fra Hamilton - Jacobi -ligningen . Fordelen med denne tilnærmingen er at den likestiller partikkels bevegelse med forplantning av en bølge, og leder pent inn i avledningen av nedbøyning av lys ved gravitasjon i generell relativitet , gjennom Fermats prinsipp . Den grunnleggende ideen er at deler av en bølgefront nærmere en gravitasjonsmasse beveger seg langsommere enn de som er lengre unna, på grunn av tyngdekraften i tiden, og dermed bøyer retningen for bølgefrontens forplantning.
Ved bruk av generell kovarians kan Hamilton - Jacobi -ligningen for en enkelt partikkel av enhetsmasse uttrykkes i vilkårlige koordinater som

Dette tilsvarer den hamiltonske formuleringen ovenfor, med de delvise derivatene av handlingen som tar stedet for det generaliserte momenta. Ved å bruke Schwarzschild metriske g μν , blir denne ligningen

hvor vi igjen orienterer det sfæriske koordinatsystemet med baneplanet. Tiden t og den azimutale vinkelen φ er sykliske koordinater, slik at løsningen for Hamiltons hovedfunksjon S kan skrives

hvor og er de konstante generaliserte momenta. Den Hamilton-Jacobi ligning gir en integrert løsning for den radiale del



Tar derivatet av Hamiltons hovedfunksjon S med hensyn til bevarte momentum p φ utbytter

som er lik

Å ta en uendelig variasjon i φ og r gir den grunnleggende orbitallikningen

hvor de konserverte lengdeskalaene a og b er definert av de bevarte momenta av ligningene

Hamiltons prinsipp
Den handling integral for en partikkel bare påvirkes av tyngdekraften er

hvor er riktig tid og er en jevn parameterisering av partikkels verdenslinje. Hvis man bruker beregningen av variasjoner på dette, får man igjen likningene for en geodesikk. For å forenkle beregningene tar man først variasjonen av kvadratet til integranden. For metrikk og koordinater for dette tilfellet og forutsatt at partikkelen beveger seg i ekvatorialplanet , er kvadratet




Å ta variasjon av dette gir
![{\ displaystyle \ delta \ left (c {\ frac {d \ tau} {dq}} \ right)^{2} = 2c^{2} {\ frac {d \ tau} {dq}} \ delta {\ frac {d \ tau} {dq}} = \ delta \ left [\ left (1-{\ frac {r _ {\ rm {s}}} {r}} \ right) c^{2} \ left ({ \ frac {dt} {dq}} \ høyre)^{2}-{\ frac {1} {1-{\ frac {r _ {\ rm {s}}} {r}}}} \ venstre ({\ frac {dr} {dq}} \ right)^{2} -r^{2} \ left ({\ frac {d \ varphi} {dq}} \ right)^{2} \ right] \ ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e86f4747c7f0f42efa826e262657c065f5b51d2)
Bevegelse i lengdegrad
Varier med hensyn til lengdegrad bare for å få


Del på for å få variasjonen av selve integranden


Og dermed

Integrering av deler gir
![0 = -{\ frac {r^{{2}}} {c}} {\ frac {d \ varphi} {d \ tau}} \ delta \ varphi -\ int {{\ frac {d} {dq} } \ venstre [-{\ frac {r^{{2}}} {c}} {\ frac {d \ varphi} {d \ tau}} \ høyre] \ delta \ varphi dq} \ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/102ff196cc6f6db3d1ffe2de3b20869363391073)
Variasjonen av lengdegraden antas å være null ved endepunktene, så det første begrepet forsvinner. Integralen kan gjøres null ved et pervers valg av med mindre den andre faktoren inne er null overalt. Så bevegelsesligningen er

![{\ frac {d} {dq}} \ venstre [-{\ frac {r^{{2}}} {c}} {\ frac {d \ varphi} {d \ tau}} \ høyre] = 0 \ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671632b4ff69e89141117984215edd0cff34d3f)
Bevegelse i tide
Varier med hensyn til tiden bare for å få


Del på for å få variasjonen av selve integranden


Og dermed

Integrering av deler gir
![{\ displaystyle 0 = c \ left (1-{\ frac {r _ {\ rm {s}}} {r}} \ right) {\ frac {dt} {d \ tau}} \ delta t- \ int { {\ frac {d} {dq}} \ venstre [c \ venstre (1-{\ frac {r _ {\ rm {s}}} {r}} \ høyre) {\ frac {dt} {d \ tau} } \ høyre] \ delta tdq} \ ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e624938aaeaf72e990427a78b54a1b65b16e10)
Så bevegelsesligningen er
![{\ displaystyle {\ frac {d} {dq}} \ venstre [c \ venstre (1-{\ frac {r _ {\ rm {s}}} {r}} \ høyre) {\ frac {dt} {d \ tau}} \ høyre] = 0 \ ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a883ea36c8f927bf91a9dd7f61c77a34a29ad825)
Bevarte momenta
Integrer disse bevegelsesligningene for å bestemme konstantene for integrering som får

Disse to ligningene for bevegelseskonstantene (vinkelmoment) og (energi) kan kombineres for å danne en ligning som er sann selv for fotoner og andre masseløse partikler som den riktige tiden langs en geodesikk er null for.



Radial bevegelse
Erstatter

og

inn i den metriske ligningen (og bruk ) gir


som man kan utlede fra

som er bevegelsesligningen for . Avhengigheten av på kan bli funnet ved å dele dette med




å få

som er sant selv for partikler uten masse. Hvis lengdeskalaer er definert av

og

da avhengigheten av på forenkler til



Se også
Merknader
-
^ Denne substitusjonen av u med r er også vanlig i klassiske sentralstyrkeproblemer, siden det også gjør disse ligningene lettere å løse. For mer informasjon, se artikkelen om det klassiske sentralstyrkeproblemet .
-
^ I den matematiske litteraturen er K kjent som den komplette elliptiske integralen av den første typen ; For mer informasjon, se artikkelen om elliptiske integraler .
Referanser
-
^
Kozai, Yoshihide (1998). "Utvikling av himmelsk mekanikk i Japan". Planet. Space Sci . 46 (8): 1031–36. Bibcode : 1998P & SS ... 46.1031K . doi : 10.1016/s0032-0633 (98) 00033-6 .
-
^ Landau og Lifshitz, s. 299–301.
-
^ Whittaker 1937.
-
^ Landau og Lifshitz (1975), s. 306–309.
-
^ Gibbons, GW; Vyska, M. (29. februar 2012). "Anvendelsen av Weierstrass elliptiske funksjoner på Schwarzschild null geodesics" . Klassisk og kvantegravitasjon . 29 (6). arXiv : 1110.6508 . doi : 10.1088/0264-9381/29/6/065016 .
-
^ Synge, s. 294–295.
-
^ arXiv.org: gr-qc/9907034v1.
-
^
Kommunikasjonsfysikk (13. august 2021) [ https://twitter.com/CommsPhys/status/1426227181731160069 "@ebi_karimi et al. Rapporterer forvrengning av lokaliserte informasjonsbærere, som skyldes buet romtiden geometri, da de fritt transporteres langs en general geodesic "] Twitter.com
-
^ Exirifard, Qasem; Culf, Eric; Karimi, Ebrahim (2021), "Towards Communication in a Curved Spacetime Geometry", Communications Physics , 4 (171), arXiv : 2009.04217 , doi : 10.1038/s42005-021-00671-8
-
^ Sean Carroll : Forelesningsnotater om generell relativitet , kapittel 7, ekv. 7.33
-
^ Weinberg, s. 122.
-
^ Einstein, s. 95–96.
-
^ Weinberg, s. 185–188; Wald, s. 138–139.
-
^ Synge, s. 290–292; Adler, Bazin og Schiffer, s. 179–182; Whittaker, s. 390–393; Pauli, s. 167.
-
^ Lanczos, s. 331–338.
-
^ Landau og Lifshitz, s. 306–307; Misner, Thorne og Wheeler, s. 636–679.
Bibliografi
- Schwarzschild, K. (1916). Über das Gravitationsfeld eines Massenpunktes nach der Einstein'schen Theorie. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1 , 189–196.
- Schwarzschild, K. (1916). Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1 , 424- ?.
-
Flamm, L (1916). "Beiträge zur Einstein'schen Gravitationstheorie". Physikalische Zeitschrift . 17 : 448– ?.
-
Adler, R; Bazin M; Schiffer M (1965). Introduksjon til generell relativitet . New York: McGraw-Hill Book Company. s. 177 –193. ISBN 978-0-07-000420-7.
-
Einstein, A (1956). Betydningen av relativitet (5. utg.). Princeton, New Jersey: Princeton University Press. s. 92 -97. ISBN 978-0-691-02352-6.
-
Hagihara, Y (1931). "Teori om de relativistiske banene i et gravitasjonsfelt av Schwarzschild". Japanese Journal of Astronomy and Geophysics . 8 : 67–176. ISSN 0368-346X .
-
Lanczos, C (1986). The Mechanics Variational Principles (4. utg.). New York: Dover Publications. s. 330–338. ISBN 978-0-486-65067-8.
-
Landau, LD ; Lifshitz, EM (1975). Den klassiske feltteorien . Kurs i teoretisk fysikk . Vol. 2 (revidert 4. engelske utg.). New York: Pergamon Press. s. 299–309. ISBN 978-0-08-018176-9.
-
Misner, CW ; Thorne, K & Wheeler, JA (1973). Gravitasjon . San Francisco: WH Freeman. s. Kapittel 25 (s. 636–687), §33,5 (s. 897–901) og §40,5 (s. 1110–1116). ISBN 978-0-7167-0344-0.(Se Gravitasjon (bok) .)
-
Pais, A. (1982). Subtil er Herren: Vitenskapen og livet til Albert Einstein . Oxford University Press. s. 253–256 . ISBN 0-19-520438-7.
-
Pauli, W (1958). Relativitetsteori . Oversatt av G. Field. New York: Dover Publications. s. 40 –41, 166–169. ISBN 978-0-486-64152-2.
-
Rindler, W (1977). Essensiell relativitet: spesiell, generell og kosmologisk (revidert 2. utg.). New York: Springer Verlag. pp. 143 -149. ISBN 978-0-387-10090-6.
-
Roseveare, N. T (1982). Merkur's perihelion, fra Leverrier til Einstein . Oxford: University Press. ISBN 0-19-858174-2.
Eksterne linker
-
Utdrag fra Reflections on Relativity av Kevin Brown.








































































































![{\ displaystyle {\ frac {d ^{2} u} {d \ varphi ^{2}}} = {\ frac {r _ {\ rm {s}}} {2}} \ venstre [\ venstre (u- u_ {2} \ høyre) \ venstre (u-u_ {3} \ høyre)+\ venstre (u-u_ {1} \ høyre) \ venstre (u-u_ {3} \ høyre)+\ venstre (u- u_ {1} \ høyre) \ venstre (u-u_ {2} \ høyre) \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbff935c41511467f9e16003f2e913b861a3216b)











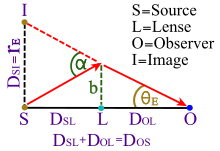





![{\ displaystyle {\ frac {1} {2}} m \ left ({\ frac {dr} {d \ tau}} \ right)^{2} = \ left [{\ frac {E^{2}} {2mc^{2}}}-{\ frac {1} {2}} mc^{2} \ right]+{\ frac {GMm} {r}}-{\ frac {L^{2}} { 2 \ mu r^{2}}}+{\ frac {G (M+m) L^{2}} {c^{2} \ mu r^{3}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78fa7da802311c62479b99d4078fbaef08a0dbf0)




![{\ displaystyle V (r) = {\ frac {\ mu c^{2}} {2}} \ venstre [-{\ frac {r _ {\ rm {s}}} {r}}+{\ frac { a^{2}} {r^{2}}}-{\ frac {r _ {\ rm {s}} a^{2}} {r^{3}}} \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/532ca22c56a1612492c5e868274d9257f0eba729)
![{\ displaystyle F =-{\ frac {dV} {dr}} =-{\ frac {\ mu c^{2}} {2r^{4}}} \ venstre [r _ {\ rm {s}} r ^{2} -2a^{2} r+3r _ {\ rm {s}} a^{2} \ right] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417d63a6c334cbf801d43b95f97d09f8b58ebd7b)
![{\ displaystyle {\ begynne {justert} r _ {\ tekst {ytre}} & = {\ frac {a^{2}} {r _ {\ rm {s}}}} \ venstre (1+{\ sqrt {1 -{\ frac {3r _ {\ rm {s}}^{2}} {a^{2}}}}} \ høyre) \\ [3pt] r _ {\ text {inner}} & = {\ frac { a^{2}} {r _ {\ rm {s}}}} \ venstre (1-{\ sqrt {1-{\ frac {3r _ {\ rm {s}}^{2}} {a^{2 }}}}}} \ right) = {\ frac {3a^{2}} {r _ {\ text {ytre}}}} \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52992e7a17eae29b6c05d60f99a6bd2d9af795bc)
![{\ displaystyle {\ begynne {justert} r _ {\ tekst {ytre}} og \ ca {\ frac {2a^{2}} {r _ {\ rm {s}}}} \\ [3pt] r _ {\ tekst {indre}} og \ ca {\ frac {3} {2}} r _ {\ rm {s}} \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df56aeae454867cb6038bbf8a624a9b34d171a92)




![\ omega _ {r}^{2} = {\ frac {1} {m}} \ venstre [{\ frac {d^{2} V} {dr^{2}}} \ høyre] _ {r = r _ {\ mathrm {ytre}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894cef5f743b66cd47bfe665608a9fff3e703799)

![{\ displaystyle \ omega _ {r} = \ omega _ {\ varphi} \ venstre [1-{\ frac {3r _ {\ rm {s}}^{2}} {4a^{2}}}+{\ matematikk {O}} \ venstre ({\ frac {r _ {\ rm {s}}^{4}} {a^{4}}} \ høyre) \ høyre]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a71fab0af7c17cf18e5c949ccb3bb3c3bedfc6c4)



![{\ displaystyle {\ begynne {justert} \ Gamma _ {rt}^{t} =-\ Gamma _ {rr}^{r} & = {\ frac {r _ {\ rm {s}}} {2r (r -r _ {\ rm {s}})}} \\ [3pt] \ Gamma _ {tt}^{r} & = {\ frac {r _ {\ rm {s}} (r-r _ {\ rm {s }})) {2r^{3}}} \\ [3pt] \ Gamma _ {\ phi \ phi}^{r} & = (r _ {\ rm {s}}-r) \ sin^{2} (\ theta) \\ [3pt] \ Gamma _ {\ theta \ theta}^{r} & = r _ {\ rm {s}}-r \\ [3pt] \ Gamma _ {r \ theta}^{\ theta} = \ Gamma _ {r \ phi}^{\ phi} & = {\ frac {1} {r}} \\ [3pt] \ Gamma _ {\ phi \ phi}^{\ theta} & =- \ sin (\ theta) \ cos (\ theta) \\ [3pt] \ Gamma _ {\ theta \ phi}^{\ phi} & = \ cot (\ theta) \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ebd981ec7f21f8385ffc13af5084c04f17ae29f)







![{\ displaystyle {\ begin {align} 0 & = {\ frac {d^{2} \ theta} {dq^{2}}}+{\ frac {2} {r}} {\ frac {d \ theta} {dq}} {\ frac {dr} {dq}}-\ sin \ theta \ cos \ theta \ venstre ({\ frac {d \ phi} {dq}} \ høyre)^{2} \\ [3pt] 0 & = {\ frac {d^{2} \ phi} {dq^{2}}}+{\ frac {2} {r}} {\ frac {d \ phi} {dq}} {\ frac {dr } {dq}}+2 \ cot \ theta {\ frac {d \ phi} {dq}} {\ frac {d \ theta} {dq}} \\ [3pt] 0 & = {\ frac {d^{2 } t} {dq^{2}}}+{\ frac {1} {w}} {\ frac {dw} {dr}} {\ frac {dt} {dq}} {\ frac {dr} {dq }} \\ [3pt] 0 & = {\ frac {d^{2} r} {dq^{2}}}+{\ frac {1} {2v}} {\ frac {dv} {dr}} \ venstre ({\ frac {dr} {dq}} \ høyre)^{2}-{\ frac {r} {v}} \ venstre ({\ frac {d \ theta} {dq}} \ høyre)^{ 2}-{\ frac {r \ sin^{2} \ theta} {v}} \ venstre ({\ frac {d \ phi} {dq}} \ høyre)^{2}+{\ frac {c^ {2}} {2v}} {\ frac {dw} {dr}} \ venstre ({\ frac {dt} {dq}} \ høyre)^{2} \ end {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7c637c4ac82e06d91b30a2a2a9286d4b52ce5f6)


![{\ displaystyle {\ begin {align} 0 & = {\ frac {d} {dq}} \ venstre [\ ln {\ frac {d \ phi} {dq}}+\ ln r^{2} \ right] \ \ [3pt] 0 & = {\ frac {d} {dq}} \ venstre [\ ln {\ frac {dt} {dq}}+\ ln w \ høyre], \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd6b6cb65149f9e94e2aaed1743e7adf905c0aa9)






![{\ displaystyle {\ begin {align} {\ frac {d} {d \ tau}} \ left [r^{2} {\ frac {d \ varphi} {d \ tau}} \ right] & = 0, \\ {\ frac {d} {d \ tau}} \ venstre [\ venstre (1-{\ frac {r _ {\ rm {s}}} {r}} \ høyre) {\ frac {dt} {d \ tau}} \ høyre] & = 0, \ ende {justert}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ec20bcaa6c2888ba4c6bac76901c7e22fa92be)






















![{\ displaystyle \ delta \ left (c {\ frac {d \ tau} {dq}} \ right)^{2} = 2c^{2} {\ frac {d \ tau} {dq}} \ delta {\ frac {d \ tau} {dq}} = \ delta \ left [\ left (1-{\ frac {r _ {\ rm {s}}} {r}} \ right) c^{2} \ left ({ \ frac {dt} {dq}} \ høyre)^{2}-{\ frac {1} {1-{\ frac {r _ {\ rm {s}}} {r}}}} \ venstre ({\ frac {dr} {dq}} \ right)^{2} -r^{2} \ left ({\ frac {d \ varphi} {dq}} \ right)^{2} \ right] \ ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e86f4747c7f0f42efa826e262657c065f5b51d2)




![0 = -{\ frac {r^{{2}}} {c}} {\ frac {d \ varphi} {d \ tau}} \ delta \ varphi -\ int {{\ frac {d} {dq} } \ venstre [-{\ frac {r^{{2}}} {c}} {\ frac {d \ varphi} {d \ tau}} \ høyre] \ delta \ varphi dq} \ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/102ff196cc6f6db3d1ffe2de3b20869363391073)

![{\ frac {d} {dq}} \ venstre [-{\ frac {r^{{2}}} {c}} {\ frac {d \ varphi} {d \ tau}} \ høyre] = 0 \ ,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671632b4ff69e89141117984215edd0cff34d3f)



![{\ displaystyle 0 = c \ left (1-{\ frac {r _ {\ rm {s}}} {r}} \ right) {\ frac {dt} {d \ tau}} \ delta t- \ int { {\ frac {d} {dq}} \ venstre [c \ venstre (1-{\ frac {r _ {\ rm {s}}} {r}} \ høyre) {\ frac {dt} {d \ tau} } \ høyre] \ delta tdq} \ ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e624938aaeaf72e990427a78b54a1b65b16e10)
![{\ displaystyle {\ frac {d} {dq}} \ venstre [c \ venstre (1-{\ frac {r _ {\ rm {s}}} {r}} \ høyre) {\ frac {dt} {d \ tau}} \ høyre] = 0 \ ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a883ea36c8f927bf91a9dd7f61c77a34a29ad825)










